Строение земляного полотна железной дороги

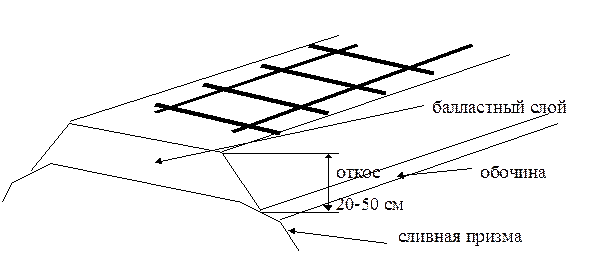
Рисунок 210- Строение земляного полотна железной дороги

Основной частью ж/д полотна является верхнее строение - рельсы со шпалами, уложенные на балластный слой (рис.210). Для лучшего стока воды земляное основание под балластным слоем устраивают в виде так называемой сливной призмы. На однопутных дорогах, ширина земляного полотна которых равна в песчаных грунтах 5.8 м, в глинистых - 6.5 м. Сливная призма в сечении имеет трапецеидальную форму с верхним основанием 2.30 м. и высотой 0.15 м. На двух путных дорогах шириной 10 м сливная призма строится с треугольным основанием, равным половине ширины полотна, и высотой 0.20 м. Вдоль ж/д полотна устраивают боковые водоотводные канавы - кюветы.

Стандартная длина рельсов 25 м. Ширина колеи - расстояние между рабочими гранями головки рельсов, обращенных внутрь пути 1524 мм (для узкоколейных - 1000-750 мм) (рис. 211).

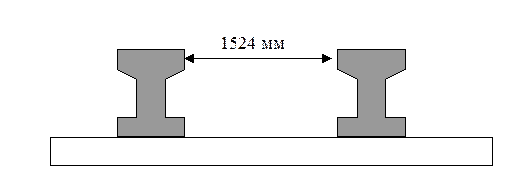
Рисунок 211.

Тип рельсов определяют по данным службы ж/д путей (например, Р38, Р43, Р65, Р75 с высотой головки рельсов от 135 до 192 мм и шириной головки рельса от 38 до 75 мм).

2.1.6.2. Разбивка соединений и парковок железнодорожных путей

А) Примыкания путей.

Примыкания, как и любые соединения железнодорожных путей, осуществляют при помощи стрелочных переводов, которые стремятся расположить на прямых участках пути. Основными частями стрелочного перевода являются (рис. 212): остряки 1 с переводным механизмом 2, переводная кривая 3 и крестовина 4. Угол между рабочими гранями крестовины называется углам крестовины. Выражение 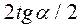называют маркой стрелки и обозначают через 1/N. По малости угла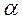

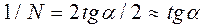(1)

На грузовых линиях наиболее распространена марка стрелочных переводов 1/9 ( 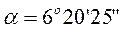), а на пассажирских линиях 1/11 ( 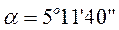), 1/22 ( ) .

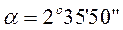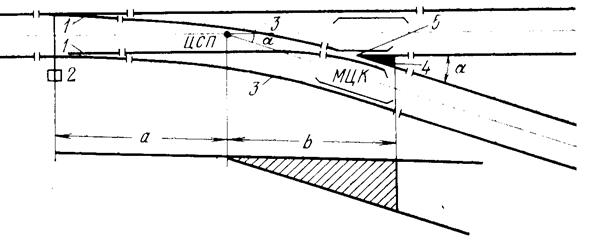
Рисунок 212 - Стрелочный перевод

Точка 5 (см. рис. 212) пересечения граней крестовины называется математическим центром крестовины (МЦК), пересечение осей двух соединяющихся путей - центром стрелочного перевода (ЦСП). Расстояния а от центра стрелочного перевода до начала стрелки и b до конца крестовины, а также до других частей стандартны и приводятся в таблицах для всех марок стрелочных переводов и типов рельсов. При разбивке стрелочного перевода на местности фиксируют положение его центра, от которого по известным размерам размещают все его элементы.

Для разбивки примыкания трассируемого пути CL (рис. 213, а) к существующему АК находят точку пересечения осей путей В и измеряют угол примыкания .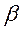

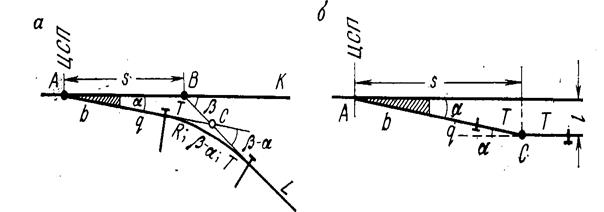
Рисунок 213 - Примыкание железнодорожных путей:

а) под углом 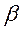; б) параллельных путей

Так как стрелочный перевод отклоняет путь на постоянный угол 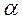, то для соединения путей CL и ВК необходимо центр стрелочного перевода разместить не в вершине угла примыкания В, а в некоторой точке А. Расстояние АВ = s может быть найдено из решения треугольника АВС, в котором известны все три угла: 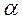, 180° - 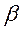, 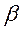- 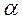и сторона AC=b+q+Т,

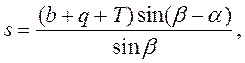(2)

где угол 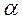и величина b определяются по марке перевода; угол 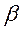измеряют на местности, прямая вставка q задается, тангенс Т берут из таблиц кривых по углу поворота 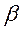- 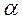и принятому радиусу R или вычисляют

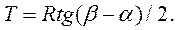(3)

Отложив по оси пути от точки примыкания В отрезок s, получили точку А - центр стрелочного перевода. Для нахождения на местности положения вершины угла поворота С откладывают вдоль трассируемой линии расстояние ВС, величина которого определяется из треугольника АВС

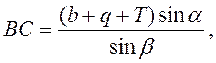(3)

Эту же точку можно определить, если в центре стрелочного перевода построить угол крестовины 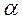и вдоль стороны АС полученного угла отложить расстояние b+q+Т.

Угол поворота трассы в вершине С равен 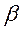- 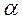. Таким образом, общий угол примыкания путей с учетом угла отклонения, который задает стрелочный перевод, будет равен сумме углов 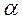и 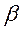- 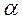, т.е. равен углу .

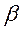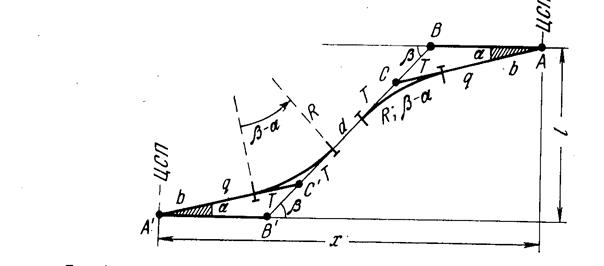
Рисунок 214 - Разбивка съезда между параллельными путями

Если место установки стрелочного перевода задано, то в этом случае разбивка примыкания производится в обратном порядке. Сначала в заданном центре стрелочного перевода А откладывают угол 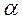соответственно марке принятой стрелки, затем находят точку С пересечения найденного направления с разбиваемой трассой и измеряют угол поворота. Если трассируемая линия проходит сравнительно далеко, то угол поворота выбирают с таким расчетом, чтобы удобно было соединиться с трассой. В обоих случаях радиус кривой на повороте назначают по возможности большим, однако величина 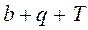не должна превышать расстояния от центра стрелочного перевода до установленной вершины угла поворота.

При примыкании параллельных путей расстояние от центра стрелочного перевода А до вершины угла поворота С (рис. 213,б )

,

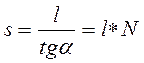где l -расстояние между осями путей. Угол поворота в точке С равен углу крестовины 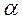. Следовательно тангенс кривой равен:

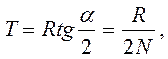
а прямая вставка равна:

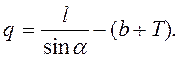
Соединение параллельных путей может быть решено при помощи съездов (см. рис. 214). При однотипных стрелочных переводах и одинаковых радиусах кривых положение второго ЦСП А’ относительно первого А находится проектированием съезда на ось абсцисс (ось первого пути)

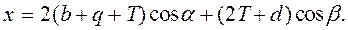
Проекция съезда на ось ординат составит

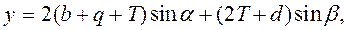
откуда величина прямой вставки вычисляется по формуле

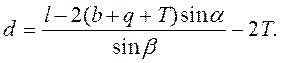
Для вычисления по этим формулам величин d и x расстояние l между осями путей и угол примыкания 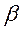измеряют на местности или берут с крупномасштабного плана , по которому проектируют съезд. Угол крестовины 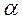и величину b определяют по марке перевода. Величину вставки q задают в зависимости от того, насколько это позволяют условия местности.

При разбивке съезда в натуре находят положение центров стрелочных переводов А и А’ (один из них находится по пикетажу пути, другой по координатам x и y). После построения в этих точках угла крестовины 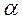и отложения расстояния 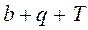определяют вершины углов поворота С и С’. Расстояние между этими вершинами с точностью до 1:2000 должно быть равно 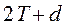, что является контролем разбивочных работ.

Б) Стрелочная улица

Стрелочная улица – это железнодорожный путь, на котором располагается ряд стрелочных переводов для ответвления параллельных путей, создающих парк путей (рис. 215).

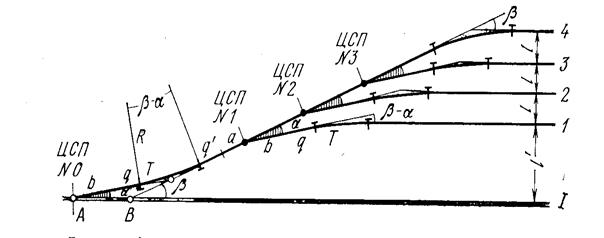
Рисунок 215 -Стрелочная улица

Для разбивки стрелочной улицы вначале под углом крестовины 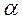к главному пути от начального стрелочного перевода откладывают :величину b, прямую вставку q и длину тангенса T. В найденной вершине поворота строят угол 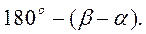Получают направление стрелочной улицы, вдоль которой, согласно проекту, разбивают стрелочные переводы.

При разбивке примыканий путей и стрелочных улиц особое внимание следует обратить на то, чтобы центры переводов располагались строго на осях путей или стрелочных улиц. Предельное отклонение центра стрелочного перевода от оси (поперечная ошибка) не должно превышать 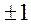см.

В) Парки путей.

К разбивке парков путей предъявляют два основных требования:

-центры всех стрелочных переводов на стрелочной улице должны располагаться на одной прямой линии;

-оси всех путей парка должны быть параллельными.

Рисунок 216 - Парк путей

Вынесенные в натуру стрелочные улицы и парки путей тщательно закрепляют, чтобы точками разбивки можно было пользоваться не только при возведении земляного полотна , но и при укладке путей. Наиболее тщательно закрепляют центры стрелочных переводов и вершины углов поворота. Эти точки одной или двумя створными плоскостями крепятся за пределами зоны земляных работ.

На земляном полотне дополнительно разбивают положение габаритных столбиков, обозначающих полезную длину путей, в пределах которой возможна стоянка вагонов. Габаритные столбики устанавливают на середине междупутья , в местах, где расстояние между осями сходящихся путей равно 4,10 м, т.е. достаточно для безопасного прохождения подвижного состава мимо стоящего вагона.

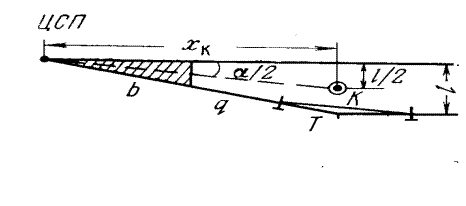
Рисунок 217 -Определение положения габаритного столбика

Согласно рис.217, координаты габаритного столбика К относительно ближайшего ЦСП будут:

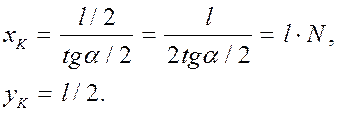
Г) Поворотные устройства.

Для поворота состава на устраивают поворотные треугольники или поворотные петли.

Поворотные треугольники. Основными данными для разбивки поворотного треугольника служат координаты x_D и y_D (рис. 218) центра стрелочного перевода D, расположенного в вершине треугольника. Эти координаты задаются относительно центров стрелочных переводов А и А’, положение которых находят по пикетажу основного пути.

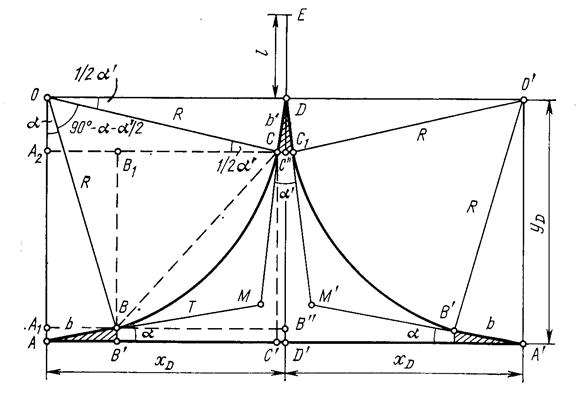
Рисунок 218 - Разбивка поворотного треугольника

Точные координаты точки D определяются как проекция ломаной АBCD соответственно на ось абсцисс и ось ординат:

При разбивке поворотного треугольника на местности по пикетажу основного пути находят точку А - центр начального стрелочного перевода. Отложив от этой точки по оси пути абсциссу x_D и под прямым углом ординату y_D , находят положение центра стрелочного перевода тупика D. Затем отмеряя по оси основного пути от точки D’ абсциссу x_D, получают точку А’- центр второго стрелочного перевода.

Если в точках А и А’ построить угол крестовины 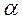и отложить величины b и 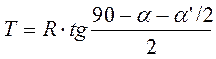, то определится положение вершин углов поворота М и М’, т.е. будут найдены все главные точки, необходимые для разбивки поворотного треугольника.

Для контроля в точке D следует измерить углы MDD’ и M’DD’ и отрезки DM и DM’. В пределах точности измерений эти углы должны быть равны 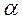’/2 , а отрезки - величине b+T . Точки M, M’ и D могут быть несколько смещены, чтобы указанные равенства были соблюдены.

Детальная разбивка криволинейных участков производится от точек BB’ и C, С’, являющихся началом и концом кривых. Ось DE тупика разбивается как продолжение направления DD’ (по биссектрисе угла ’).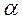

Поворот на 180° с помощью петли. Правоповоротная петля состоит из прямого участка AG = x, основной кривой DEFG, прямой вставки DC, обратной соединяющей кривой CB, которая соединяет стрелочный перевод с прямым участком (рис. 219).

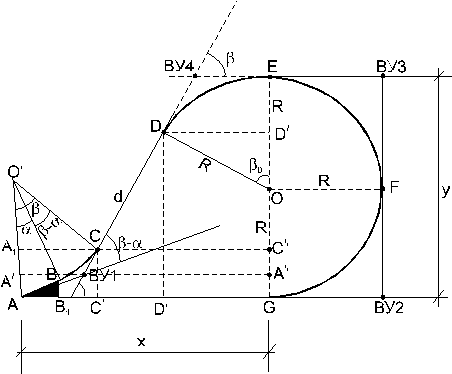
Рисунок 219 – Поворот с помощью петли

Выполним необходимые расчеты:

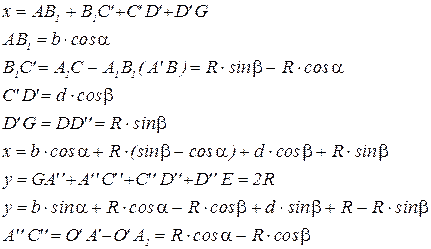
Угол b определяется из проекции характерных точек поворотной петли на ось y.

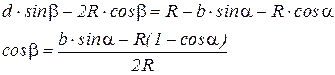
Разбивку поворотной петли начинают с определения положения стрелочного перевода А. Затем на местности разбивают вершины углов поворота ВУ1, ВУ2, ВУ3, ВУ4 и конечные точки кривых B, C, D, F, E, G. От них производят детальную разбивку петли.