Коллизий задач за базовые процессоры в данном примере не возникает.
Пример 4.2. Положим, исходные условия те же, что и в примере 4.1, но необходимо максимизировать коэффициент загрузки 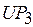 базового процессора типа 3.
базового процессора типа 3.
Поскольку условные ветвления процессов вычислений отсутствуют (см. рис. 1), то 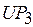 – частный вид критерия (2.7) и представляет собой отношение суммарного времени использования соответствующего процессора к крайнему сроку завершения задания
– частный вид критерия (2.7) и представляет собой отношение суммарного времени использования соответствующего процессора к крайнему сроку завершения задания 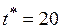 .
.
Допустим, коллизии разрешаются за счет незадействованного базового процессора типа 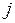 , введение которого в состав ресурсов сопровождается минимальным значением штрафной функции стоимости
, введение которого в состав ресурсов сопровождается минимальным значением штрафной функции стоимости 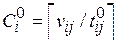 .
.
Максимум загрузки процессора 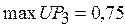 обеспечивается распределениями, диаграммы которых показаны на рис. 4.
обеспечивается распределениями, диаграммы которых показаны на рис. 4.
При этом в случаях, иллюстрируемых рис. 4, а и 4, в, возникают коллизии, вызванные конкуренцией задач 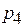 и
и 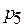 за единственный базовый процессор третьего типа. Поскольку оптимальные длительности выполнения этих задач одинаковы и равны
за единственный базовый процессор третьего типа. Поскольку оптимальные длительности выполнения этих задач одинаковы и равны 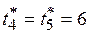 , то с позиций загрузки базового процессора не имеет значения, какой из них отдать преимущество в его использовании: загрузка процессора после разрешения коллизии не изменяется. Самым «дешевым» является введение процессора типа 4 (см. табл. 1). Однако задача
, то с позиций загрузки базового процессора не имеет значения, какой из них отдать преимущество в его использовании: загрузка процессора после разрешения коллизии не изменяется. Самым «дешевым» является введение процессора типа 4 (см. табл. 1). Однако задача 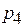 не может быть на нем реализована, поскольку
не может быть на нем реализована, поскольку 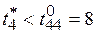 . Поэтому на этот процессор назначается задача
. Поэтому на этот процессор назначается задача 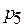 , при этом
, при этом 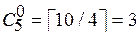 – минимальное из возможных значений функции штрафа.
– минимальное из возможных значений функции штрафа.
Заметим, что в штрафной функции 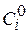 , в отличие от (2.6), вместо времени, отведенного для выполнения
, в отличие от (2.6), вместо времени, отведенного для выполнения 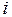 -й задачи, фигурирует априорная оценка
-й задачи, фигурирует априорная оценка 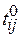 . Дело в том, что коэффициент загрузки процессоров при равенстве длительности выполнения конкурирующих задач оказывается нечувствительным к введению процессора, тип которого отличается от типа процессора, за который эти задачи конкурируют. В подобных случаях для оценки качества распределения полезно использовать вторичный показатель эффективности в виде функции штрафа
. Дело в том, что коэффициент загрузки процессоров при равенстве длительности выполнения конкурирующих задач оказывается нечувствительным к введению процессора, тип которого отличается от типа процессора, за который эти задачи конкурируют. В подобных случаях для оценки качества распределения полезно использовать вторичный показатель эффективности в виде функции штрафа 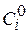 . А вот если в качестве критерия оптимальности использовать функцию стоимости вида (2.5) или (2.6), то при таком разрешении коллизий не обеспечивается ее минимум. Иными словами, соотношение (3.7) теоремы 1 не выполняется.
. А вот если в качестве критерия оптимальности использовать функцию стоимости вида (2.5) или (2.6), то при таком разрешении коллизий не обеспечивается ее минимум. Иными словами, соотношение (3.7) теоремы 1 не выполняется.
Дата добавления: 2020-10-01; просмотров: 543;











