ОСНОВЫ ГИДРАВЛИКИ. ГИДРОСТАТИКА

Основные понятия. Гидравликой называется прикладная наука, изучающая законы равновесия и движения жидкостей и способы их практического использования.

Жидкостью в физике считается тело, обладающее текучестью. Вследствие слабых связей между собой частицы жидкости обладают высокой степенью подвижности. Поэтому жидкое тело в отличие от твердого не имеет собственной формы и принимает форму сосуда, в котором оно находится.

Гидравлика состоит из двух основных разделов: гидростатики и гидродинамики. В гидростатике рассматриваются законы равновесия жидкостей, в гидродинамике - законы их движения.

С точки зрения гидравлики под термином «жидкость» понимают не только жидкие, но и газообразные тела. В связи с этим жидкости делят на капельные и газообразные.

В гидравлике преимущественно рассматриваются капельно-жидкие тела, характеризующиеся очень малой сжимаемостью. Однако при давлениях, близких к атмосферному, и газы, которые характерны большой сжимаемостью при повышении давления, ведут себя как практически несжимаемые жидкости и подчиняются основным законам гидравлики.

Особенности движения газов при иных давлениях и температурах, когда заметно проявляются их отличия от капельных жидкостей, изучаются в аэродинамике и газовой динамике.

Физические свойства жидкостей. В гидравлике используются основные свойства жидкостей, изучаемые в курсах физики, а именно удельный вес, плотность, сжимаемость, тепловое расширение и вязкость, которые кратко рассмотрены ниже. Как и все физические величины, характеристики этих свойств могут измеряться в различных системах единиц измерения, из которых наиболее распространена Международная система (СИ) как более универсальная.

Удельным (или объемным) весом g жидкости называют вес жидкости в единице объема, т. е. отношение

g = G /V, (1)

где G - вес (сила тяжести) определенного количества (определенной массы) жидкости;

V - объем этого количества жидкости.

Размерность удельного веса в соответствии с формулой (1) равна отношению единицы силы к единице объема, т. е. Н/м³.

Плотность р жидкости представ­ляет величину ее массы в единице объема:

r = M/V, (2)

где М - масса жидкости в объеме V.

Размерность плотности - кг/м³. Так как вес (сила тяжести) и масса тела связаны между собой на основании второго закона Ньютона (G = Mg, где g - 9,81 м/с² - ускорение свободного падения), то аналогично связаны между собой удельный вес и плотность:

g = r • g (3)

Отсюда r = g/g- Поэтому размерность плотности представляет отношение размерностей удельного веса и ускорения.

Удельный объем v - объем единицы массы - величина, обратная плотности:

v = V/M = l/r (4)

Его единица — м³/кг.

Удельный вес, плотность и удельный объем капельных жидкостей и газов не являются постоянными величинами, они зависят от давления и температуры. При повышении температуры жидкости ее удельный вес и плотность уменьшаются, а удельный объем увеличивается. Тепловое расширение жидкостей характеризуется температурным коэффициентом объемного расширения b_t который равен отношению приращения объема DV к первоначальному объему Vo и приращению температуры Dt(при постоянном давлении):

1 DV

b_t = --- • ----- (5)

Dt Vo

Размерность b_t обратна размерности температуры.

Из формулы (5) можно определить приращение объема жидкости при нагревании:

DV = b_t • Vo • Dt (6)

Для капельных жидкостей величина b_t относительно невелика (для воды b_t = 0,0004 при температуре 20 - 100 °С) и приращение их объема при нагревании незначительно. Но все же нагревание воды в системе дизеля, объем которой составляет более 1200 л, от 20 до 90°С изменяет эту величину на 40 л. Газы вообще характерны высокими значениями b_t.

При повышении давления удельный вес и плотность жидкости увеличиваются, а удельный объем уменьшается. Сжимаемость жидкостей характеризуется коэффициентом объемного сжатия b_р, который равен относительному уменьшению объема жидкости на единицу приращения давления Dр при неизменяемой температуре:

1 DV

b_р = - --- • -----

D_р Vo

где DV - изменение объема (минус в формуле указывает на его уменьшение).

Размерность b_р обратна размерности давления.

Уменьшение объема жидкости при сжатии

DV= - b_р • Vo • D_р (8)

Величина р_р для капельных жидкостей также очень мала (b_р = 0,0005, если давление измеряется в МПа), поэтому сжимаемостью капельных жидкостей обычно можно пренебрегать (их считают в гидравлике несжимаемыми). Необходимо отметить также, что жидкости практически не сопротивляются растяжению.

Вязкость - свойство жидкости оказывать сопротивление относительному перемещению её частиц.

Предположим, жидкость (масло) заполняет тонкий зазор между вращающимся валом А и неподвижным подшипником Б (рис. 2.1). Опыт показывает, что частицы жидкости, непосредственно соприкасающиеся с граничными стенками, как бы прилипают к ним и имеют одинаковую с ним скорость. Следовательно, слой жидкости, примыкающий к валу А, будет перемещаться со скоростью вала u, а слой, соприкасающийся с подшипником, будет неподвижен. Таким образом, скорость промежуточных слоев жидкости в зазоре будет различной и каждый из них будет перемещаться (сдвигаться) относительно соседних слоев. Внутреннее трение в жидкости оказывает сопротивление такому сдвигу с силой F по площади сдвига S.

Удельная сила трения t («тау») - напряжение сдвига:

F

Рис. 2.1. Внутреннее трение в слое жидкости

где m («мю») - динамическая вязкость; Du/Dh - градиент скорости в слое жидкости: отношение разности скоростей смежных слоев жидкости (Du = u₁ – u₂) к расстоянию Dh между ними (см. рис. 2.1).

Единица измерения m - Н • с/м², или Па • с. Эта единица очень значительна по своему размеру. Поэтому применяют дольную единицу - миллипаскаль-секунду (мПа • с).

В гидравлике используется также понятие кинематической вязкости v («ню»):

n = m/r, (10)

где r - плотность жидкости.

Единица измерения n - м²/с. Вязкость характеризует степень подвижности частиц жидкости. Вода имеет низкую вязкость, нефтепродукты (различные масла, дизельное топливо) отличаются более высокой вязкостью.

Вязкость жидкостей уменьшается при повышении их температуры.

Вязкие свойства и сжимаемость жидкостей значительно усложняют рассмотрение многих вопросов их движения. Поэтому в гидравлике часто пользуются понятием идеальной жидкости, т. е. условной жидкости, не обладающей вязкостью и абсолютно несжимаемой. Такая жидкость имеет постоянную плотность, не обладает внутренним трением и, следовательно, не оказывает сопротивления перемещению. Идеальных жидкостей в природе не бывает, но использование этого понятия облегчает выяснение основных закономерностей гидравлики, используя которые применительно к реальным жидкостям, необходимо учитывать поправки на их вязкость и сжимаемость.

Основное уравнение гидростатики. В открытом сосуде с жидкостью, находящейся в покое (рис. 2.2, а), представим мысленно на глубине h площадку DS и рассмотрим условия ее равновесия. Для этого выделим элемент объема жидкости, расположенный над площадкой (рис. 2.2, б), заменив его связи с окружающим пространством внешними силами.

В горизонтальном направлении на боковую поверхность цилиндра действуют силы давления окружающей его жидкости. Они уравновешиваются как равные и противоположно направленные.

В вертикальном направлении на элемент действуют: сила внешнего давления P = p₀DS, где p₀ - внешнее давление на свободную поверхность жидкости (для открытого сосуда - атмосферное давление p_а = p₀); сила тяжести G массы жидкости в объеме элемента (G =g • h • DS=r • g • h • DS).

Обе эти силы действуют вниз. Однако элемент, как и вся жидкость в сосуде, находится в равновесии. Такое равновесие возможно лишь при наличии уравновешивающей силы R, действующей на площадку со стороны остального объема жидкости, т. е. снизу вверх. Эту распределенную по площадке силу можно представить, так же как и силу внешнего давления, в виде произведения давления на площадь: R = p • DS. Величина p = R/DS носит название гидростатического давления.

Гидростатическое давление характерно двумя важными свойствами: оно всегда направлено перпендикулярно к площадке, на которую действует; величина гидростатического давления в любой точке объема жидкости не зависит от положения (угла наклона) площадки, на которую оно действует (иными словами, в данной точке оно одинаково по всем направлениям).

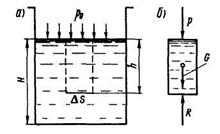Рис. 2.2. К выводу основного уравнения гидростатики:

а - сосуд с жидкостью; б - элемент объема жидкости

Условием равновесия выделенного объема в вертикальном направлении будет уравнение R — P—G = 0 или

p • DS — p₀ • DS — r • g • h • DS = 0. Отсюда

p = p_o + r • g • h = p_o+ g • h. (11)

Уравнение (11) называют основным уравнением гидростатики. Оно показывает, что гидростатическое давление в любой точке внутри жидкости равно давлению на ее свободную поверхность, сложенному с давлением столба жидкости, высота которого равна глубине точки, в которой измеряется давление.

Гидростатическое давление по формуле (11) называют полным, или абсолютным.

Избыточное (или манометрическое) давление

p_из6 = p - p_o = p • g • h = g • h. (12)

Измерение давления. Как видно из уравнения (12), избыточное давление совпадает с давлением столба жидкости. Это совпадение указывает на простой и удобный способ измерения небольших избыточных давлений - по высоте столба жидкости.

Простершим прибором такого типа является пьезометр (рис. 2.3, а) - вертикальная прозрачная трубка, присоединенная к сосуду с жидкостью своим нижним концом. Верхний конец трубки открыт. Если в сосуде давление атмосферное - уровни жидкости в нем и в трубке будут одинаковы. Если же в сосуде давление выше атмосферного, столб жидкости в трубке будет выше уровня в сосуде на высоту h, которая называется пьезометрической высотой и является по уравнению (12) мерой избыточного давления. Этот же способ используется в общеизвестном U-образном манометре (рис. 2.3, б), применяемом обычно для измерений малых давлений в воздушных и газовых потоках. Если высота трубки в таких приборах не превышает 1 м, то наибольшее избыточное давление, которое можно измерить, не превышает 10 кПа. Для измерений больших давлений применяют манометры с ртутью, удельный вес которой в 13,6 раза больше удельного веса воды. Это позволяет или увеличить диапазон измеряемых давлений, или уменьшить высоту трубок. Для измерения разности давлений Dh в разных сосудах или в различных участках трубопровода применяют дифференциальные манометры (рис. 2.3,.в).

Для измерения высоких давлений применяют металлические манометры (пружинные и мембранные).

Закон Паскаля. Из основного уравнения гидростатики (11) следует, что внешнее давление, приложенное к свободной поверхности жидкости, находящейся в ограниченном сосуде, передается в любую точку жидкости без изменения. Иными словами давление, приложенное в каком-то участке замкнутой гидравлической системы, сообщается всей жидкости, находящейся в системе.

Это положение, называемое законом Паскаля, широко используется в технике в различных гидравлических устройствах, предназначенных для «выигрыша» в силе (грузоподъемные устройства, домкраты, прессы) или передачи силы на расстояние (гидропривод). Устройства, основанные на законе Паскаля, широко применяются и в тепловозостроении. Это, например, гидравлическое управление иглой форсунки дизеля, гидростатический привод вентиляторов, сервомотор регулятора частоты вращения вала дизеля и т. п.

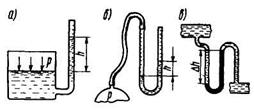
Рис 2 3 Измерение гидростатического давления

а - пьезометр, б - U-образный манометр, в - дифференциальный манометр

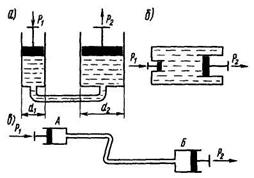Рис 2 4 Схемы гидростатического привода

Принципы их действия иллюстрируются схемами рис. 2.4. Если соединить два цилиндра диаметрами d₁ и d₂, заполненные жидкостью (рис. 2.4, а), или просто расположить два разных поршня в одном резервуаре (рис. 2.4, б), то, приложив силу Р₁ к поршню малого цилиндра, мы создадим во всей системе давление p = 4P_l/(nd²₁). Под действием этого давления поршень большого цилиндра при перемещении способен преодолеть гораздо большее усилие:

Р₂ = r ----

значение которого зависит от квадрата соотношения диаметров этих цилиндров. Так, например, устроены гидравлические домкраты. На основе этого принципа создаются гидравлические прессы, способные развивать колоссальные усилия (тысячи и десятки тысяч тонн).

Схема (рис. 2.4, в) показывает передачу управляющего усилия на расстояние: приложив силу Р₁ к поршню цилиндра А, соединенного трубопроводом с цилиндром Б, мы заставим перемещаться его поршень, несмотря на то, что цилиндры могут быть удалены друг от друга.

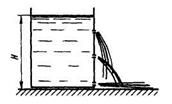
Рис. 2.5. К определению давления жидкости на вертикальную стенку

Давление жидкости на стенку сосуда в соответствии с основным законом гидростатики неодинаково по высоте.

Это наглядно видно на примере вертикального резервуара (рис. 2.5). Если просверлить в его боковой стенке несколько отверстий на разной высоте, то мы увидим, что вода будет вытекать из них в горизонтальном направлении и дальность струи будет тем больше, чем ниже отверстие. Этот опыт подтверждает также, что вода оказывает именно боковое давление на стенку, перпендикулярное к ее поверхности. Если требуется определить силу давления жидкости на плоскую стенку сосуда, то необходимо иметь в виду, что на уровне свободной поверхности давление на стенку равно внешнему давлению р_о(h = О), а на дно сосуда давление p = p_o + r • g • Н. Так как гидростатическое давление по уравнению (11) линейно зависит от глубины, то, чтобы вычислить силу давления на всю стенку, достаточно определить среднее давление: p_cp = p₀ + pgH/2 и умножить его на площадь стенки.

2.2. ГИДРОДИНАМИКА

Движущуюся массу жидкости для возможности анализа закономерностей движения в гидродинамике считают состоящей из отдельных элементарных струй, каждая из которых перемещается, не смешиваясь с другими Совокупность элементарных струй представляет поток жидкости. Потоки характеризуются живым сечением и расходом.

Живым сечением потока называется поверхность, перпендикулярная в каждой точке сечения направлению течения жидкости в этой точке. В общем случае, когда направления движения в отдельных элементарных струйках различны, живое сечение представляет криволинейную поверхность. Если направления одинаковы - живое сечение 1-2-3-4-1 будет плоским (рис. 2.6, а). Но даже в плоском живом сечении скорости течения v₁ в отдельных струйках, хотя и направлены одинаково, но различны по величине в отдельных точках (а, b, ..., i, .... п) этого сечения. Картина распределения скоростей по сечению называется полем скоростей.

Живое сечение характеризуют следующие параметры:

площадь живого сечения S, определяемая как часть поперечного сечения канала, ограничивающего поток жидкости, занятой ею (площадь l • h на рис. 2.6, а);

смоченный периметр c («каппа») - часть периметра поперечного сечения канала (1-2-3-4), которая .омачивается жидкостью;

гидравлический радиус R = S/c, Представляющий отношение площади живого сечения к смоченному периметру. Для круглой трубы гидравлический радиус равен четверти ее диаметра.

Расходом называется количество жидкости, протекающее через живое сечение в единицу времени. Различают объемный расход Q (м³/с) и массовый М (кг/с):

М = r • Q. (13)

Средняя скорость потока v пред­ставляет собой частное от деления объемного расхода на площадь жи­вого сечения (м/с):

v = Q/S. (14)

Зная среднюю скорость потока, можно определить объемный расход жидкости в нем

Q = v • S. (15)

Потоки жидкости могут иметь различный характер движения. Движение называют установившимся, если в каждой точке потока величины скорости, давления и температуры жидкости (различные в разных точках) с течением времени не меняются. Несоблюдение любого из условий делает движение потока неустановившимся.

Установившееся движение называется равномерным, если поток по всей длине имеет одинаковые живые сечения и, следовательно, скорости.

Уравнение неразрывности потока. Если в установившемся потоке жидкости выделить сечения А я Б (рис. 2.6, б), то объемные расходы жидкости в этих сечениях Q_A = v_A • S_A и Q_Б = v_Б • S_Б должны быть одинаковы, так как поток сплошной, в нем нет никаких пустот, жидкость несжимаема, и между этими сечениями она никуда не расходуется и ниоткуда не поступает.

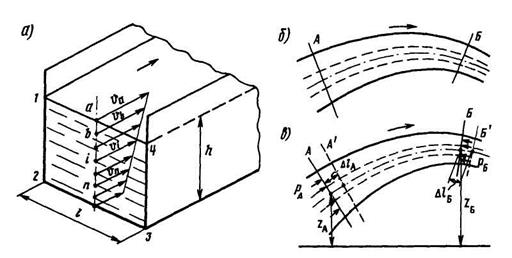
Рис. 2.6. Схемы потока жидкости

Отсюда следует, что и в других сечениях неразветвленного потока расходы жидкости должны быть также одинаковы. Следовательно,

Q = v_A • S_A = const. (16)

Уравнение (16) называется уравнением неразрывности потока, или уравнением постоянства расхода. По существу оно выражает общеизвестный закон сохранения массы.

Из этого уравнения следует, что v_A/v_Б — S_Б/S_a,т. е. средние скорости потока обратно пропорциональны площадям его живых сечений. Например, если диаметр трубы увеличить в два раза, скорость потока уменьшится в 4 раза.

Уравнение Бернулли. Рассмотрим состояние элемента установившегося потока идеальной жидкости между сечениями А и Б (см. рис. 2.6, б) через малый промежуток времени Dt (рис. 2.6, в). Ограничивающие его сечения за это время переместятся: А — в положение А' на расстояние Dl_A=v_A • Dt, а Б - в положение Б' на расстояние Dl_b = v_B • Dt.

Определим изменение кинетической энергии рассматриваемого элемента потока при перемещении его из положения АБ в положение А'Б'. Очевидно, что кинетическая энергия основной части объема между сечениями А' и Б не меняется. Различаться могут лишь кинетические энергии частей объема между сечениями А и А', которую рассматриваемый элемент освобождает при течении, и между сечениями Б и Б', занимаемой вновь.

Из механики известно, что кинетическая энергия движущегося тела равна половине произведения массы его на квадрат скорости (Екин = mv²/2). Кинетическая энергия элемента объема между сечениями А и А' равна

Е^Акин = r • Q • Dt • a_А • v²/2, (17)

где r • Q • Dt = M • Dt = m - масса жидкости в объеме элемента АА'; a_А - коэффициент Кориолиса. Этот коэффициент компенсирует неточность, которая возникает, если кинетическую энергию рассчитывать по средней скорости потока (действительная кинетическая энергия равна сумме кинетических энергий отдельных струй потока). Безразмерный коэффициент а представляет отношение действительной кинетической энергии к ее значению, рассчитанному по средней скорости. Значения a зависят от неравномерности скоростей потока по сечению и обычно лежат в пределах 1 - 1,10. Поэтому часто величиной a в расчетах пренебрегают. Аналогично для элемента ББ'

Е^Бкин = r • Q • Dt • a_Б • v²/2, (18)

Разность этих величин, или измене­ние кинетической энергии,

DЕкин = 0,5 • r • Q • Dt • (a_Б • v²_B - a_Б • v²_A). (19)

Изменение энергии тела, как следует из механики, равно работе внешних сил. Такими силами для элемента потока являются силы тяжести и силы гидростатического давления на торцовые сечения элемента.

Работа силы тяжести равна произведению веса тела на величину его перемещения по вертикали. Согласно уравнению постоянства расхода (16) массы частей потока АА' и ББ' одинаковы. Их вес равен r • g • Q • Dt , а перемещение по вертикали - разности ординат z_A - z_Б. Тогда работа силы тяжести

DЕ_g = r • g • Q • Dt • (z_A - z_Б). (20)

Давления на торцы объема различны по величине (р_А ¹ р_Б) и противоположны по знаку (+РА и — Р_Б), так как давление р_ъ препятствует течению потока.

Работа сил давления DЕ_Р = p_A • S_A • Dl_A - p_B • S_B • Dl_B.

Произведения S_A • Dl_A и S_B • Dl_B представляют собой части объема между сечениями А—А' и Б—Б'. По уравнению постоянства расхода они одинаковы и равны каждое Q • Dt (например, S_A • Dl_A = S_A • v_A • Dt = Q • Dt).

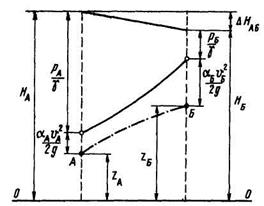
Рис 2 7 Графическая иллюстрация закона Бернулли

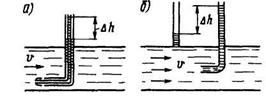
Рис. 2.8. Измерение скорости потока жидкости

Тогда

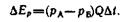(21) Так как

то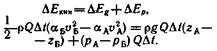

Разделим все члены этого выражения на вес рассматриваемого элемента потока 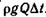, т. е. будем рассматривать удельную энергию на единицу веса. Тогда получим (имея в виду, что ):

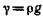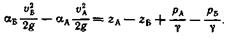
После перестановки членов имеем

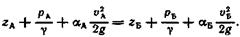(22)

Выражение (22) называется уравнением Бернулли для идеальной жидкости. Это одно из важнейших уравнений гидравлики, оно в 1738 г. впервые было установлено известным ученым Даниилом Бернулли, членом Российской Академии наук.

Так как выполненное рассуждение можно провести и для любых других сечений и элементов потока, то уравнение (2.22) можно записать в более общем виде:

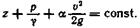(23)

Выражение (23) применительно к движению идеальной жидкости выражает закон сохранения энергии. Оно говорит о том, что удельная энергия в установившемся потоке идеальной жидкости постоянна, она не может ни увеличиваться, ни уменьшаться. Изменение одного из слагаемых должно неизбежно приводить к изменению других слагаемых.

Рассмотрим подробнее слагаемые удельной энергии в уравнениях, (22) и (23). Все они имеют линейную размерность (м). Для слагаемого 2 это очевидно, но нетрудно убедиться в этом и для других слагаемых:

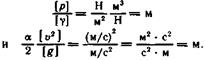
Первый член уравнения (23) представляет геометрическую высоту (геометрический напор) рассматриваемого сечения потока над выбранным уровнем сравнения, для которого

2 = 0.

Второй член - это гидростатическое давление, выраженное высотой столба жидкости.

Третий член уравнения выражает кинетическую энергию потока и называется скоростным (или динамическим) напором.

Таким образом, каждое слагаемое - это отдельный вид удельной энергии: z - удельная энергия высоты (или положения); 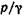- удельная энергия давления; 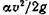- удельная кинетическая энергия.

Сумма всех слагаемых может быть названа полной удельной энергией потока Н (полным напором).

Следовательно, уравнение Бернулли можно представить в простом виде:

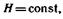(24) имея в виду, что

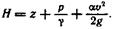(25)

Из последнего уравнения, в частности, следует, что при увеличении скорости течения жидкости давление в потоке уменьшается и, наоборот, уменьшение скорости потока вызывает повышение давления в нем.

Это положение называют законом Бернулли.

Уравнения (22) - (25) получены для жидкости, не имеющей вязкости. При течении реальной жидкости вследствие ее вязкости часть энергии затрачивается на преодоление трения (внутреннего – между отдельными струями потока и внешнего - о стенки канала). Эта часть энергии, как и всякая работа сил трения, преобразуется в тепловую энергию и рассеивается в окружающую среду, т. е. для механической энергии потока теряется безвозвратно. Поэтому для реальной жидкости нельзя ограничиваться рассмотрением только механической энергии, для нее закон сохранения энергии надо рассматривать в общем виде. Однако чтобы не вводить чрезмерных усложнений, можно представить потерянную часть механической энергии в виде дополнительной потери давления потока вследствие трения. Тогда уравнение Бернулли для реальной жидкости можно представить на основе уравнения (22), включив в правую часть четвертое слагаемое DН_АБ, представляющее собой необратимую потерю энергии, связанную с преодолением сопротивлений течению потока на участке АБ:

(26)

Таким образом, полная удельная энергия потока реальной жидкости в любом сечении равна полной удельной энергии в любом предшествующем сечении за вычетом потерь давления на участке потока между этими сечениями:

Н_А = Н_Б + DН_АБ. (27)

Рассмотрим некоторые частные случаи уравнения (26). Если поток движется горизонтально (z_А = z_Б), уравнение приобретает вид

Ра , «а»а _ Рв , "в"1 , . —-т--2£ — + ~2]Г+^ЛЯАБ-

(28)

Из выражения (28) видно, что в этом случае уменьшение скорости течения (например, если v_B<v_fi вследствие увеличения диаметра трубопровода) может привести к увеличению статического давления в точке Б по сравнению с точкой А.

Если же жидкость течет в горизонтальном канале одинакового сечения (трубе), то v_а = v_б. Уравнение существенно упрощается: р_А — р_Б = g • DН_АБ, т. е. в этом случае разность давлений в двух точках представляет потерю давления на трение между этими точками.

Ввиду того что все члены уравнения Бернулли имеют линейную размерность, его можно наглядно представить графически, как это сделано на рис. 2.7 для участка потока АБ (см. рис. 2.6). Точки А и Б на рис. 2.7 обозначают центры тяжести соответствующих сечений, а отрезки ординат, измеренные от условного уровня О—0, - частные и полные удельные энергии потока.

Уравнение Бернулли имеет очень широкое применение в гидравлической технике. На его основе рассчитываются гидравлические системы и машины. Оно также служит основой для проведения измерений в потоках жидкости, например для измерений скоростей, расхода и т. п.

Наиболее простым устройством для измерения местной (локальной) скорости жидкости является трубка Пито-Прандтля (рис. 2.8, а), представляющая комбинацию пьезометра и трубки Пито с изогнутым концом, направленной навстречу потоку (рис. 2.8, б). Трубка Пито показывает полный напор жидкости в потоке (p/g + n²/2g), а пьезометрическая трубка - статический напор р/g. Таким образом, разность уровней в трубках Dh соответствует динамическому напору v²/2g. Следовательно, скорость жидкости в точке измерения

v = krj2g\h, (2.29)

где k - тарировочный коэффициент, учитывающий вязкость жидкости и особенности конструкции и установки трубки.

Изменяя положение трубки по высоте, можно установить распределение скоростей жидкости по сечению и вычислить среднюю скорость, по которой определяется расход жидкости.

2.3. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ

Гидравлические сопротивления.

При течении жидкости по трубам ей приходится затрачивать энергию на преодоление сил внешнего и внутреннего трения. В прямых участках труб эти силы сопротивления действуют по всей длине потока и общая потеря энергии на их преодоление прямо пропорциональна длине трубы. Такие сопротивления называются линейными. Их величина (потеря давления) зависит от плотности и вязкости жидкости, а также от диаметра трубы (чем меньше диаметр, тем больше сопротивление), скорости течения (увеличение скорости увеличивает потери) и чистоты внутренней поверхности трубы (чем больше шероховатость стенок, тем больше сопротивление).

Кроме трения в прямых участках, в трубопроводах встречаются дополнительные сопротивления в виде поворотов потока, изменений сечения, кранов, ответвлений и т. п. В этих случаях структура потока нарушается и его энергия затрачивается на перестроение, завихрения, удары. Такие сопротивления называют местными. Линейные и местные сопротивления являются двумя разновидностями так называемых гидравлических сопротивлений, определение которых составляет основу расчета любых гидравлических систем.

Режимы течения жидкости. В практике наблюдаются два характерных режима течения жидкостей: ламинарный и турбулентный.

При ламинарном режиме элементарные струйки потока текут параллельно, не перемешиваясь. Если в такой поток ввести струйку окрашенной жидкости, то она будет продолжать свое течение в виде тонкой нити среди потока неокрашенной жидкости, не размываясь. Такой режим течения возможен при очень малых скоростях потока. С увеличением скорости выше определенного предела течение становится турбулентным, вихреобразным, при котором жидкость в пределах поперечного сечения трубопровода интенсивно перемешивается. При постепенном увеличении скорости окрашенная струйка в потоке сначала начинает колебаться относительно своей оси, затем в ней появляются разрывы из-за перемешивания с другими струями и затем вследствие этого весь поток получает равномерную окраску.

Наличие того или иного режима течения зависит от величины отношения кинетической энергии потока (1/2mv² = 1/2rVv²) к работе сил внутреннего трения (Fl = \iS^rl)—см.

(.9).

Это безразмерное отношение 1/2рУЪ²/ (\iS-ry-l) можно упростить, имея в виду, что Аи пропорционально v. Величины I u Dh также имеют одну и ту же размерность, и их можно сократить, а отношение объема V к поперечному сечению S является линейным размером d.

Тогда отношение кинетической энергии к работе сил внутреннего трения с точностью до постоянных множителей можно характеризовать безразмерным комплексом:

Re = J^-=il (30)

который называется числом (или критерием) Рейнольдса в честь английского физика Осборна Рейнольдса, в конце прошлого века экспериментально наблюдавшего наличие двух режимов течения.

Малые значения чисел Рейнольдса свидетельствуют о преобладании работы сил внутреннего трения в потоке жидкости и соответствуют ламинарному течению. Большие значения Re соответствуют преобладанию кинетической энергии и турбулентному режиму течения. Граница начала перехода одного режима в другой - критическое число Рейнольдса - составляет

Re_KР z 2300

для круглых труб (в качестве характерного размера принимается диаметр трубы).

В технике, в том числе и тепловозной, в гидравлических (в том числе воздушных и газовых) системах обычно имеет место турбулентное течение жидкостей. Ламинарный режим бывает лишь у вязких жидкостей (например, масло) при малых скоростях течения и в тонких каналах (плоские трубки радиатора).

Расчет гидравлических сопротивлений.

Линейные потери напора определяются по формуле Дарси-Вейсбаха:

^д//<=41г ⁽²³¹⁾

где к («лямбда») — коэффициент линейного сопротивления, зависящий от числа Рейнольдса. Для ламинарного потока в круглой трубе k = 64/Re (зависит от скорости), для турбулентных потоков величина X мало зависит от скорости и, главным образом, определяется шероховатостью стенок труб.

Местные потери напора также считаются пропорциональными квадрату скорости и определяются так:

ДЯ_г = £-|р (32)

где £ (дзета») - коэффициент местного сопротивления, зависящий от типа сопротивления (поворот, расширение и т. п.) и от его геометрических характеристик.

Коэффициенты местного сопротивления устанавливаются опытным путем, их значения приводятся в справочниках.

Понятие о расчете гидравлических систем. При расчете любой гидравлической системы решается обычно одна из двух задач: определение необходимого перепада давлений (напора) для пропуска данного расхода жидкости или определение расхода жидкости в системе при заданном перепаде давлений.

В любом случае должна быть определена полная потеря напора в системе АН, которая равна сумме сопротивлений всех участков системы, т. е. сумме линейных сопротивлений всех прямых участков трубопроводов и местных сопротивлений других элементов системы:

+² (Иг)- ⁽³³⁾

что расход жидкости постоянен дли всех элементов системы (без ответвлений). Подставив в условие (33) значения v = Q/S, получим

*»-*&&}+* $&>)-•*■

(2.35)

*—*И-И)+*(*)]-

гидравлическая характеристика, или общий коэффициент сопротивления системы.

Необходимо иметь в виду, что расчет трубопроводов не является решением задачи с одним определенным ответом. Его результаты зависят от выбора величины диаметров участков трубопровода или скоростей в них. Действительно, можно принять в расчете невысокие значения скоростей и получить небольшие потери напора. Но тогда при заданном расходе сечения трубопроводов (диаметры) должны быть большими, система будет громоздкой и тяжелой. Приняв высокие скорости течения в трубах, мы уменьшим их поперечные размеры, но при этом существенно (пропорционально квадрату скорости) возрастут потери напора и затраты энергии на работу системы. Поэтому при расчетах обычно задаются какими-то средними, «оптимальными», значениями скоростей течения жидкости. Для водяных систем оптимальная скорость имеет порядок примерно 1 м/с, для воздушных систем низкого давления — 8 — 12 м/с.

Гидравлический удар представляет собой явление, происходящее в потоке жидкости при быстром изменении скорости его течения (например, при резком закрытии задвижки в трубопроводе или остановке насоса). В этом случае кинетическая энергия потока мгновенно переходит в потенциальную энергию и давление потока перед задвижкой резко возрастает. Область повышенного давления затем распространяется от задвижки в сторону еще не заторможенного полностью потока со скоростью, близкой к скорости звука а в этой среде.

Резкое повышение давления приводит если не к разрушению, то к упругой деформации элементов трубопровода, что уменьшает силу удара, но усиливает колебания давления жидкости в трубе. Величина скачка давления при полной остановке потока жидкости, имевшего скорость v, определяется по формуле выдающегося русского ученого - профессора Н Е. Жуковского, полученной им в 1898 г.: &p—pva, где р - плотность жидкости. С целью предотвращения ударных явлений в крупных гидравлических системах (например, водопроводных сетях) запорные устройства выполняют так, чтобы их закрытие происходило постепенно.

2.4. НАСОСЫ И ВЕНТИЛЯТОРЫ

Насосом называется гидравлическая машина для напорного перемещения жидкости по трубопроводам и гидравлическим системам в результате сообщения жидкости энергии (кинетической и потенциальной). Вентиляторы предназначены для подачи воздуха или других газов под давлением (обычно до 0,15 МПа)., Струйные насосы представляют собой устройства для нагнетания (отсасывания) жидкой или газообразной среды, увлекаемой струей жидкости, пара или газа.

Работа насоса (вентилятора) характеризуется расходом, (подачей) Q жидкости или газа, напором (давлением) Н, к.п.д. г) и потребляемой мощ