Основные графические компоненты языка.

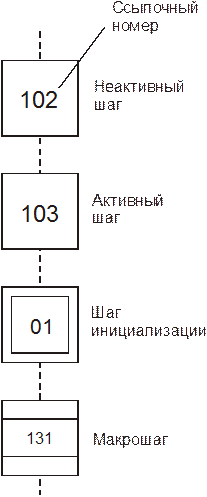
Шаг изображается одинарным квадратом. К шагам адресуются по номерам, написанным на квадратике шага. Основное описание шага записывается в прямоугольник, присоединённый к символу шага.

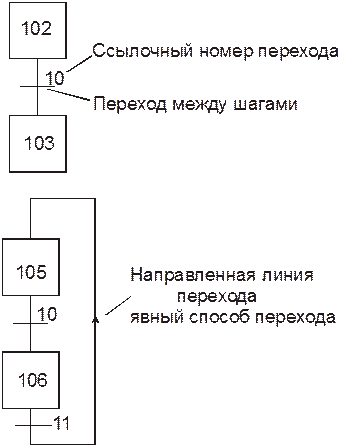
Переход изображается пересекающейся линией. Условие перехода записывается в прямоугольнике, присоединенном к нему.

Каждый шаг и переход должны иметь уникальный идентификатор, по которому к нему ссылаются из других программ. У шага по умолчанию идентификатор GSnnn, где nnn – номер шага. У перехода GTnnn.

GSnnn является сложной переменной, состоящей из 2-х компонентов:

GSnnn.х – булева переменная, обозначающая активность шага;

GSnnn.t – таймерная переменная. Время прошедшее с момента последней активации шага.

Макрошаг – это уникальная группа шагов и переходов на языке SFC, записанных отдельно и изображаемых в основной программе в виде одного символа. Сам макрошаг представляет собой автономную схему, где первый шаг не имеет верхнего соединения, т.е. к нему нет явного перехода, а конечный шаг не имеет нижнего соединения, т.е. от него нет переходов. Область его использования ограничена компактным описанием основной схемы и возможностью переноса макросов в различные программы и проекты.

Пример программы на языке SFC с макрошагом:

Ссылочный номер, записанный в символе макрошага основной схемы или программы – это ссылочный номер первого шага в теле макрошага.

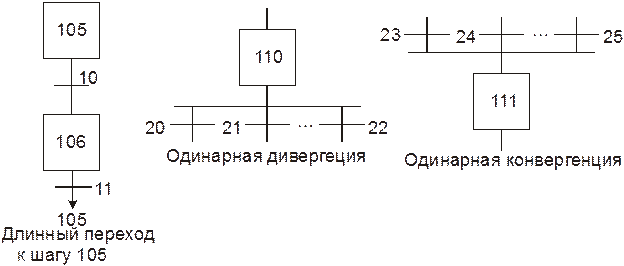
Одинарная дивергенция– это множественное соединение от одного шага к нескольким переходам. Условие переходов должно быть взаимоисключающим. Одинарная конвергенция – это множественное соединение от нескольких переходов к одному шагу. Используется, чтобы сгруппировать ветви программы, берущие начало из одинарной дивергенции.

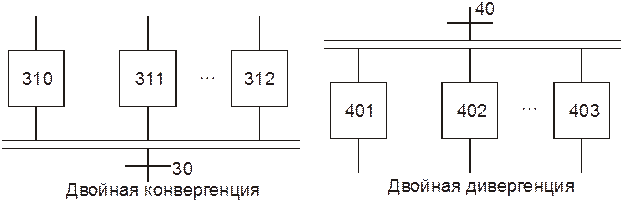
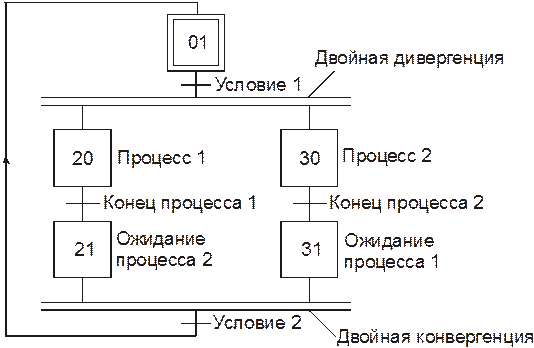
Двойная дивергенция – это множественное соединение от одного перехода к нескольким шагам, выполняемые параллельно. Двойная конвергенция – это множественное соединение от нескольких шагов к одному и тому же переходу. Используется, чтобы сгруппировать ветви программы, берущие начало в двойной конвергенции.

Пример программы на языке SFC с двойной дивергенцией и конвергенцией.