После разделения переменных
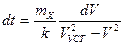
Время изменения скорости от V1 до V2 выражается определенным интегралом в соответствующих пределах
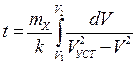 (7.12)
(7.12)
Теперь, если учесть, что 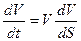 то после подстановки этого выражения в уравнение (7.10) и разделения переменных получим определенный интеграл, выражающий путь судна в процессе изменения скорости oт V1до V2
то после подстановки этого выражения в уравнение (7.10) и разделения переменных получим определенный интеграл, выражающий путь судна в процессе изменения скорости oт V1до V2
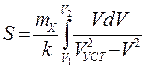 (7.13)
(7.13)
После интегрирования выражений (7.12) и (7.13) получим формулы соответственно для времени в секундах и пути в метрах при изменении скорости судна от V1до V2 {V1, V2 и VУСТ выражаются в м/с, тх — в кг, k — в кг/м):
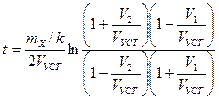 (7.14)
(7.14)
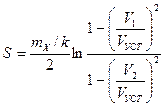 (7.15)
(7.15)
Следует отметить, что формулы (7.14) и (7.15) позволяют получить конечные решения, когда V2 имеет любое значение между значениями V1 и VУСТ, но не равное VУСТ или нулю.
Торможение судна
Тормозные характеристики судна, под которыми подразумеваются время и путь торможения в зависимости от начальной скорости, имеют важное значение для обеспечения безопасности мореплавания.
Торможение бывает пассивным и активным.
Пассивное торможение выполняется при остановленном двигателе только за счет сопротивления воды.
Активное торможение обеспечивается за счет реверсирования главного двигателя, после чего создается сила упора винта назад.
Реверс главного двигателя не может быть выполнен мгновенно, поэтому активному торможению всегда предшествует участок пассивного.
В общем случае процесс торможения принято делить на три периода.
Первый период — прохождение команды продолжается от момента подачи команды по машинному телеграфу до момента закрытия топлива на ДВС, пара на ТЗА или выключения питания ГЭД. Первый период длится недолго, примерно 5 с.
Второй период — пассивное торможение длится с момента прекращения подачи топлива (пара) на двигатель до момента реверса.
Третий период—активное торможение длится с момента реверса до момента полной остановки судна или снижения скорости до какого-то заданного значения.
Полное время Т и полный тормозной путь S определяются как суммы соответствующих элементов по трем периодам:
T=t1+t2+t3 (7.16)
S=s1+s2+s3
На судах с ВРШ началом третьего периода можно считать момент прохождения лопастями нулевого положения.
Процесс торможения судна на основании (3.1) с учетом (3.8) описывается дифференциальным уравнением вида
dV
mx-— = -kV2-Pe. (7.17)
dt
Решения записанного в общем виде уравнения (7.17) относительно времени и пути торможения зависят от конкретного вида зависимости для силы упора винта Ре, которое должно быть подставлено в это уравнение. Будем считать полезную силу упора в процессе торможения постоянной величиной, численно равной значению силы упора в режиме на швартовах, т. е.
Ре = Ршв = const. (7.18)
Коэффициент k с учетом квадратичной зависимости силы сопротивления от скорости определяется выражением:
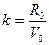 (7.19)
(7.19)
где Vo — исходное значение скорости, м/с;
Ro — полная сила сопротивления воды при скорости Vo, H.
Подстановка (7.18) и (7.19) в дифференциальное уравнение (7.17) дает
 (7.20)
(7.20)
После разделения переменных получается выражение для времени активного торможения от начальной скорости Vн до текущей V:
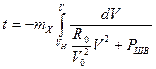 (7.21)
(7.21)
а после подстановки 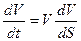 получим соответствующее выражение для тормозного пути
получим соответствующее выражение для тормозного пути
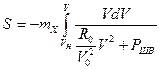 (7.22)
(7.22)
В результате интегрирования выражений (7.21) и (7.22) получены рабочие формулы для расчета времени и пути торможения (время, сек; путь, м):
для пассивного торможения (РШВ = 0):
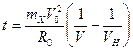 (7.23)
(7.23)
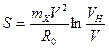 (7.24)
(7.24)
для активного торможения:
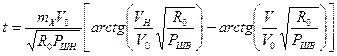 (7.25)
(7.25)
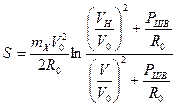 (7.26)
(7.26)
Дата добавления: 2020-08-31; просмотров: 678;











