Выбор формы и определение размеров типовых конструкций.
Одна из проблем, которые решаются при разработке конструкций ЭВМ, — сокращение потерь быстродействия из-за конечной скорости распространения сигналов по линиям межэлементных связей. Общая задержка сигналов при преобразовании информации складывается из задержек сигналов 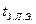 в логических элементах и времени распространения сигналов
в логических элементах и времени распространения сигналов  в линиях связи, т. е.
в линиях связи, т. е.
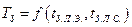
 При скорости распространения сигнала
При скорости распространения сигнала 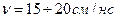 по линии связи межэлементная связь длиной 30 см дает задержку сигнала в 1,5—2 нс, что сопоставимо с задержкой быстродействующего логического элемента. Реальные потери быстродействия из-за задержек сигналов в линиях связи оказываются довольно значительными, например в вычислительных машинах фирмы «IBM» время распространения сигнала по линиям межэлементных связей составило 70-80 % длительности цикла.
по линии связи межэлементная связь длиной 30 см дает задержку сигнала в 1,5—2 нс, что сопоставимо с задержкой быстродействующего логического элемента. Реальные потери быстродействия из-за задержек сигналов в линиях связи оказываются довольно значительными, например в вычислительных машинах фирмы «IBM» время распространения сигнала по линиям межэлементных связей составило 70-80 % длительности цикла.
Длина линии связи между наиболее удаленными участками типовой конструкций зависит от ее компоновочной схемы. В связи с этим возникает задача выбора такой пространственной геометрии конструктивного модуля, которая при данном его объеме обеспечивала бы минимальную длину линии связи между наиболее удаленными элементами.
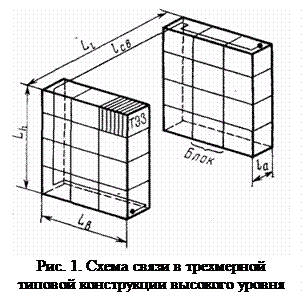
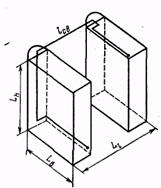
Пространственная геометрия модулей прямоугольной конструкции. Наиболее общей компоновочной схемой конструктивного модуля высокого уровня является многомерная схема, показанная на рис. 1.
По этой схеме, как правило, выполняются стойки универсальных и специальных ЭВМ. В соответствии с рисунком длина линии связи между наиболее удаленными элементами
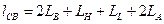 (1)
(1)
где 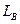 - суммарная длина блоков;
- суммарная длина блоков; 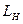 - высота стойки;
- высота стойки; 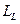 — ширина стойки;
— ширина стойки; 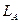 - часть линии связи, проходящая внутри блока в направлении, совпадающем с
- часть линии связи, проходящая внутри блока в направлении, совпадающем с 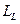 .
.
Полагая 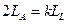 уравнение (1) запишем в виде
уравнение (1) запишем в виде
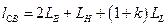 (2)
(2)
где k — коэффициент, зависящий от конструктивного обрамления блоков.
Для определения оптимального соотношения между пространственными параметрами модуля, обеспечивающего минимальную длину связи 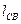 при данном его объеме
при данном его объеме 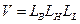 воспользуемся методом геометрического программирования Рис. 1. Полагаем, что
воспользуемся методом геометрического программирования Рис. 1. Полагаем, что 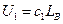 ;
; 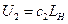 ;
; 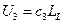 ;
; 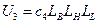 , где
, где 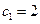 ;
; 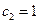 ;
; 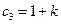 ;
; 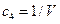 ;
; 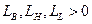 .
.
Целевая функция задачи примет вид:

при ограничении  .
.
Минимальное значение
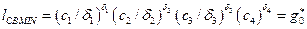 (3)
(3)
где 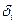 — веса, подчиняющиеся условиям ортогональности:
— веса, подчиняющиеся условиям ортогональности:  ;
; 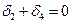 ;
; 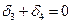 ; и условию нормализации
; и условию нормализации 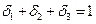 . Эти условия образуют систему из четырех линейных уравнений с четырьмя неизвестными, которая имеет единственное решение:
. Эти условия образуют систему из четырех линейных уравнений с четырьмя неизвестными, которая имеет единственное решение: 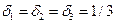 ;
; 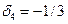 .
.
Подставив в (3) значения 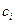 и
и 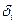 , получим:
, получим:
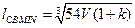 ; (4)
; (4)
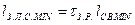 (5)
(5)
где 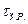 - задержка распространения сигнала на единице длины линии связи.
- задержка распространения сигнала на единице длины линии связи.
Для однорамной стойки минимальная длина линии связи 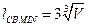 ; (6)
; (6)
В точке оптимума коэффициенты 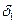 ,
, 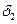 ,
, 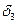 представляют собой относительные величины членов
представляют собой относительные величины членов 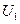 ,
, 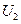 ,
, 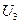 т. е.
т. е.
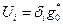 (7)
(7)
Отсюда 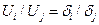 и, учитывая, что
и, учитывая, что 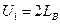 ;
; 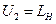 ;
; 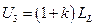 , получим оптимальное соотношение между пространственными параметрами стойки:
, получим оптимальное соотношение между пространственными параметрами стойки:
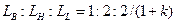 (8)
(8)
| 
|
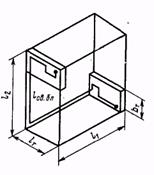
| Рис. 2. Компоновочная схема многорамной стойки | Рис. 3. Двухмерная компоновка субблоков |
При заданном значении 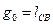 на основании (7) можно вывести формулы для расчета геометрических размеров стойки:
на основании (7) можно вывести формулы для расчета геометрических размеров стойки:
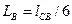 ;
; 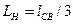 ;
; 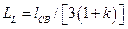 ; (9)
; (9)
где 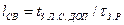 ;
; 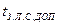 — допустимая задержка сигнала в линии связи.
— допустимая задержка сигнала в линии связи.
Выражение (5) позволяет на этапе эскизного проектирования получить оценку снизу ожидаемой задержки сигнала в линиях связи разрабатываемой типовой конструкции i-го уровня на основе априорных представлений о количестве входящих в нее элементов (i-1)-го уровня и плотности их компоновки. Анализ выражений (4) и (6) показывает, что двухмерная компоновка типовых элементов, т. е. однорамная стойка, обеспечивает меньшую длину линии связи между наиболее удаленными элементами стойки, чем трехмерная.
Решим задачу определения оптимальной геометрии функциональных устройств, размещаемых в панелях или блоках, для обеспечения минимальной потери быстродействия в линиях связи внутри них. Общей компоновочной схемой субблоков в блоках стационарных ЭВМ является двухмерная, показанная на рис. 3.
Сформулируем задачу определения оптимальной геометрии блока как задачу геометрического программирования. Длина части линии связи, проходящая внутри типового элемента замены, зависит от качества решения задачи трассировки соединений между микросхемами. В некоторых случаях при размерах типового элемента замены 140 X 150 мм длина линии связи в блоке достигает значения 600 мм. Запишем ее в виде 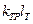 , тогда
, тогда
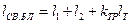 (10)
(10)
где 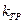 - коэффициент, учитывающий качество трассировки (при отсутствии ограничений на длину связей в ТЭЗ
- коэффициент, учитывающий качество трассировки (при отсутствии ограничений на длину связей в ТЭЗ 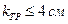 ). Объем блока
). Объем блока
 (11)
(11)
На основании (10) и (11) целевая функция задачи будет: 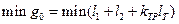 при ограничении
при ограничении 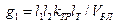 .
.
Решение задачи дает следующие результаты: минимальная длина линии связи блока
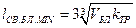 (12)
(12)
оптимальное соотношение геометрических размеров блока 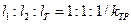 (13)
(13)
Выражения для расчета размеров 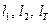 при заданном значении длины линии связи будут:
при заданном значении длины линии связи будут:
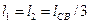 (14)
(14)
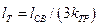 (15)
(15)
Выбор компоновочной схемы многорамной стойки (конструкция типа ЕС ЭВМ).Выше было отмечено, что при одном и том же объеме устройства однорамная конструкция стойки обеспечивает меньшую длину линии связи между наиболее удаленными микросхемами, чем многорамная. Однако при большом количестве оборудования, размещаемого в стойке, размеры платы ТЭЗ могут оказаться слишком большими и не позволят обеспечить механическую прочность и надежность ТЭЗ. Например, для устройства объемом 80 000 микросхем подсчитано, что L; = 1080 мм. При однорамной компоновке стойки это значение будет соответствовать длине ТЭЗ, а максимально допустимый размер стороны платы ТЭЗ равен 470 мм. В связи с этим стойки основных устройств универсальных ЭВМ, в которых число микросхем достигает нескольких десятков тысяч, приходится делать многорамными при большом числе блоков в раме.
Определим оптимальное соотношение 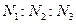 где
где 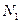 и
и 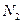 — количество вертикальных и горизонтальных рядов блоков в раме;
— количество вертикальных и горизонтальных рядов блоков в раме; 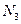 — количество рам в стойке.
— количество рам в стойке.
Для выбора компоновочной схемы многорамной стойки используем соотношение (8), приняв k = 0 на том основании, что связи между блоками являются внутрирамными. Выражение (8) примет вид
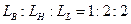 (16)
(16)
Запишем 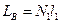 ;
; 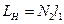 ;
; 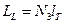 . Из формул (14) и (15) имеем
. Из формул (14) и (15) имеем 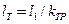 .
.
Подставив в (16) выражения для 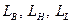 получим оптимальное соотношение
получим оптимальное соотношение
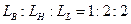 (17)
(17)
В частном случае при 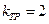 приходим к соотношению
приходим к соотношению 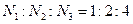 .
.
Дата добавления: 2016-07-18; просмотров: 2095;











