ОСНОВНЫЕ УРАВНЕНИЯ МАТЕРИАЛЬНОГО БАЛАНСА
Материальный баланс служит для контроля производства, регулирования состава продукции, установления производственных потерь. С помощью материального баланса можно определить экономические показатели технологических процессов и способов производства (производственные потери, степень использования составных частей молока, расход сырья, выход готового продукта)
В основе материального баланса лежит закон сохранения вещества, записанный математически в виде двух уравнений.
Первое уравнение – это баланс сырья и вырабатываемых из него продуктов
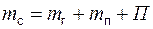 (1)
(1)
где mс, mг, mп – масса соответственно сырья, готового и побочного продуктов, кг, П – производственные потери, кг.
После переработки масса получаемых продуктов меньше массы переработанного сырья. Разницу между ними составляют производственные потери. Производственные потери выражают также в процентах от количества переработанного сырья:
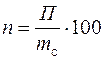
откуда
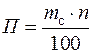
Тогда уравнение (1) примет вид
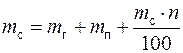 (2)
(2)
Второе уравнение материального баланса составляют по массе сухих веществ молока или отдельных составных частей
Если составные части молока не претерпевают химических изменений в ходе технологических процессов, то количество их в сырье должно быть равно количеству в готовом и побочном продуктах. Баланс составных частей молока при его переработке можно составить так:
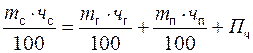 (3)
(3)
или
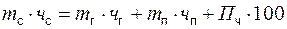
где чс, чг, чп – массовая доля составных частей молока соответственно в сырье, в готовом и побочном продуктах, %; Пч, – потери составных частей молока, кг.
Потери выражают в процентах от составных частей молока, cодержащихся в сырье:
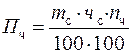
где nч – потери составных частей молока, %.
После подстановки Пч в уравнение (3) второе уравнение материального баланса примет вид
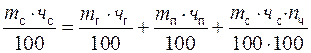
или
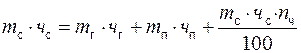 (4)
(4)
Потери составных частей молока nч и потери сырья n, выраженные в процентах, численно равны.
Баланс можно составить по любой части молока – жиру Ж, сухому остатку молока С, сухому обезжиренному молочному остатку (СОМО) О. Так, баланс по жиру при сепарировании молока
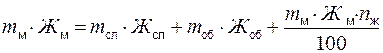
где Жм, Жсл, Жоб, – массовая доля жира соответственно в молоке, сливках и обезжиренном молоке, %; nж – потери жира при сепарировании, %
Для производства сухого и сгущенного молока баланс можно составить по сухому молочному остатку:
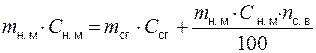 (5)
(5)
где mсг – масса сгущенного молока, кг, Сн.м, Ссг – массовая доля сухого молочного остатка соответственно в нормализованном и сгущенном молоке, %; nc.в – потери сухих веществ при производстве сгущенного молока, %.
В уравнении (5) отсутствует одно слагаемое, так как при сгущении и сушке побочный продукт (вода) не содержит сухих веществ молока.
Решая совместно первое (2) и второе (4) уравнения материального баланса, можно определить массу сырья по готовому продукту при известном составе сырья, готового и побочных продуктов или установить массу готового продукта по массе сырья:
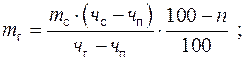 (6)
(6)
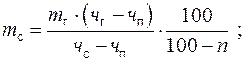 (7)
(7)
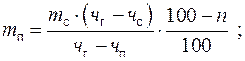 (8)
(8)
Материальные расчеты обычно проводят с учетом производственных потерь. При ориентировочных расчетах ими пренебрегают. Массу сырья готового и побочных продуктов без учета потерь определяют по формулам
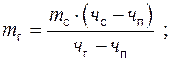 (9)
(9)
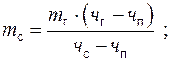 (10)
(10)
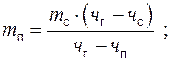 (11)
(11)
Необходимо определить массу сливок для производства 500 кг масла, если массовая доля жира в масле составляет 78 %, в сливках – 38, в пахте – 0,7%. Нормативные потери при производстве масла составляют 0,6 %.
Для решения задачи воспользуемся формулой (7):
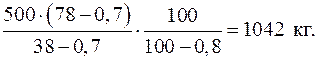
Массу готового продукта по сырью или массу сырья по готовому продукту можно определить как алгебраическим методом (по формулам), так и графическим (по расчетному треугольнику).
Сущность способа расчета с помощью треугольника состоит в следующем. В вершинах треугольника записывают массовую долю одной из составных частей молока, содержащихся в сырье чс, в готовом чг и побочном чп продукта.

 чг На внутренних сторонах треугольника
чг На внутренних сторонах треугольника
записывают значение массы сырья тс,
чг – чс чг – чп готового тги побочного mп продуктов
mп mc напротив соответствующей им массовой
им массовой доли составной части моло-
чс mг чп ка. На внешних сторонах треугольника
 чс – чп располагают величину разности между массовыми долями составных частей молока (расположенными в вершинах треугольника), полученную вычитанием из большей величины меньшей.
чс – чп располагают величину разности между массовыми долями составных частей молока (расположенными в вершинах треугольника), полученную вычитанием из большей величины меньшей.
В соответствии с правилом расчетного треугольника составляют пропорцию: отношение внутренних сторон к внешним – величина постоянная для данного треугольника:
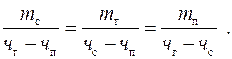
Из этого соотношения определяют необходимые величины.
Дата добавления: 2020-07-18; просмотров: 793;











