Тема 3. Основы реализации списковых структур
3.1. Структуры данных типа “линейный список”
Линейный список – это набор связанных однотипных элементов, в котором каждый элемент каким-то образом определяет следующий за ним элемент. В отличие от стека и очереди, добавление нового элемента возможно в любом месте списка, также можно удалить любой элемент списка. Ясно, что списковые структуры являются более гибкими, но и немного более сложными в реализации. Фактически, стеки и очереди можно считать частными случаями списков, в которых добавление и удаление элементов может выполняться только на концах.
Стандартный набор операций со списком включает:
· добавление нового элемента после заданного или перед заданным элементом с проверкой возможности добавления элемента
· удаление заданного элемента
· проход по списку от первого элемента к последнему с выполнением заданных действий
· поиск в списке заданного элемента
Как обычно, возможна статическая и динамическая реализация списков. При этом статическая реализация на базе массива может быть выполнена двумя способами.
3.2. Первый способ статической реализации списка.
Он основан на том, что логический номер элемента списка полностью соответствует номеру ячейки массива, где этот элемент хранится: первый элемент списка – в первой ячейке массива, второй – во второй, третий – в третьей и т.д.
| Элемент 1 | Элемент 2 | Элемент 3 | . . . . . . . | Элемент N |
Проверка наличия в массиве хотя бы одного элемента и хотя бы одной свободной ячейки выполняется элементарно с помощью счетчика числа элементов списка. Проход по списку – также элементарен. Поиск заданного элемента сводится к обычному поиску в массиве.
Как выполнить вставку нового элемента внутри списка, например – в ячейку с номером i < N ? Для освобождения ячейки i все элементы списка начиная с номера i и до N надо сдвинуть вправо на одну ячейку (конечно, если в массиве есть еще хотя бы одна свободная ячейка). Копирование надо начинать с последней ячейки, т.е. N – на место N+1, N-1 – на место N, и.т.д. i – на место i+1. В освободившуюся ячейку i записывается новый элемент.
Аналогично (с точностью до наоборот) выполняется удаление любого внутреннего элемента: освобождается ячейка i и все последующие элементы сдвигаются влево на одну ячейку, т.е. i+1 – на место i, i+2 – на место i+1, и т.д., элемент N – в ячейку N-1.
Возникает вопрос о трудоемкости выполнения подобных операций перемещения ячеек массива. Если каждый элемент списка, размещенный в одной ячейке массива представляет собой запись с большим числом объемистых полей, то затраты на подобное перемещение могут стать слишком большими. Здесь выходом может быть изменение структуры элемента списка: в массиве хранятся ТОЛЬКО УКАЗАТЕЛИ (АДРЕСА) информационных частей и перемещение производится только этих указателей, сами информационные части остаются на своих местах. Учитывая все возрастающие скорости работы современных процессоров и наличие в их архитектуре быстрых команд группового копирования байтов, можно считать данный метод реализации списков вполне работоспособным.
3.3. Второй способ статической реализации списка.
Второй способ реализации списка на основе массива использует принцип указателей (но БЕЗ динамического распределения памяти). В этом случае каждый элемент списка (кроме последнего) должен содержать номер ячейки массива, в которой находится следующий за ним элемент. Это позволяет РАЗЛИЧАТЬ физический и логический порядок следования элементов в списке. Удобно (но НЕ обязательно) в начале массива ввести фиктивный элемент-заголовок, который всегда занимает нулевую ячейку массива, никогда не удаляется и указывает индекс первого реального элемента списка. В этом случае последний элемент списка (где бы он в массиве не располагался) должен в связующей части иметь некоторое специальное значение-признак, например – индекс 0.
Схема физического размещения элементов списка в массиве:
| Номер ячейки | ||||||
| Информац. часть | заголовок | Элем. 3 | Элем. 1 | Элем. 2 | Элем. 4 | |
| Следующий эл-нт |
Соответствующая схема логического следования элементов списка:
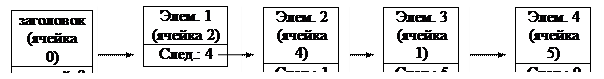 |
Тогда необходимые объявления могут быть следующими:
Const N = 100;
TypeTListItem = record
Inf : <описание>;
Next : integer;
end;
Var StatList : array [0 . . N] of TListItem;
Рассмотрим реализацию основных списковых операций.
Условие пустоты списка: StatList [ 0 ].Next = 0;
Проход по списку:
· ввести вспомогательную переменную Current для отслеживания текущего элемента списка и установить Current := StatList [ 0 ].Next;
· организовать цикл по условию Current = 0, внутри которого обработать текущий элемент StatList [ Current ].Inf и изменить указатель Current на следующий элемент: Current := StatList [ Current ].Next
Поиск элемента аналогичен проходу, но может заканчиваться до достижения конца списка:
Current := StatList [ 0 ].Next;
While (Current <> 0) and (StatList [ Current ].Inf <> ‘значение’ do
Current := StatList [ Current ].Next;
If Current = 0 then ‘поиск неудачен’ else ‘элемент найден’;
Добавление элемента после заданного:
· проверка возможности добавления с помощью счетчика текущего числа элементов в списке
· определение каким-то образом элемента, после которого надо добавить новый элемент (например – запрос у пользователя)
· поиск этого элемента в списке; пусть его индекс есть i
· определение номера свободной ячейки массива для размещения нового элемента (методы определения будут рассмотрены ниже); пусть этот номер равен j
· формирование связующей части нового элемента, т.е. занесение туда номера ячейки из связующей части элемента i : StatList [ j ].next := StatList [ i ].next;
· изменение связующей части элемента i на номер j: StatList [ i ].next := j;
· занесение данных в информационную часть нового элемента StatList[j].inf;
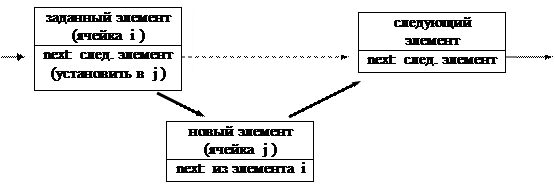
Аналогично производится добавление нового элемента перед заданным, правда здесь приходится дополнительно узнавать номер ячейки, в которой находится элемент, предшествующий заданному. Это требует небольшого изменения процедуры поиска заданного элемента: вместе с индексом искомого элемента должен определяться индекс его предшественника. Для этого вводится вспомогательная переменная целого типа, которая в процессе поиска заданного элемента “отстает” на один элемент и тем самым всегда указывает предшественника искомого элемента.
Алгоритм добавления элемента перед заданным включает следующие шаги:
· проверка возможности добавления с помощью счетчика текущего числа элементов в списке
· определение каким-то образом элемента, перед которым надо добавить новый элемент (например – запрос у пользователя)
· поиск этого элемента в списке с одновременным отслеживанием элемента-предшественника; пусть индекс заданного элемента есть i, а индекс его предшественника - s
· определение номера свободной ячейки массива для размещения нового элемента (методы определения будут рассмотрены ниже); пусть этот номер равен j
· формирование связующей части нового элемента, т.е. занесение туда индекса i : StatList [ j ].next := i;
· изменение связующей части элемента-предшественника с индекса i на индекс j: StatList [ s ].next := j;
· занесение данных в информационную часть нового элемента StatList[j].inf;

Удаление заданного элемента (естественно, в случае его наличия в списке) также требует изменения связующей части у элемента-предшественника. Это изменение позволяет “обойти” удаляемый элемент и тем самым исключить его из списка.
Необходимые шаги:
· определение каким-то образом удаляемого элемента (например – запрос у пользователя)
· поиск удаляемого элемента в списке с одновременным отслеживанием элемента-предшественника; пусть индекс удаляемого элемента есть i, а индекс его предшественника - s
· изменение связующей части элемента-предшественника с индекса i на индекс-значение связующей части удаляемого элемента i: StatList [s].next := StatList [ i ].next;
· обработка удаляемого элемента (например – вывод информационной части)
· включение удаленного элемента во вспомогательный список без его уничтожения или освобождение ячейки i с включением ее в список свободных ячеек (методы поддержки свободной памяти рассматриваются ниже)
 |
Дата добавления: 2020-07-18; просмотров: 884;











