Основные положения гидравлики

Неподвижная жидкость. Пусть имеется некоторый сосуд, наполненный водой. Внешнее давление - 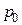. Сосуд располагается над условной плоскостью сравнения О - О (рис. 2.1). Поверхность воды в сосуде находится относительно плоскости сравнения на высоте z₀. Возьмем в жидкости произвольную точку А, находящуюся на глубине h и на расстоянии z от плоскости О - О. Тогда полное гидростатическое давление p в точке А определяется по основному уравнению гидростатики:

, (2.1)

Рис. 2.1. Схема к опре-делению гидростати-ческого напора

где 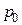- внешнее давление, действующее на свободную поверхность жидкости, Па; 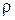- плотность жидкости, кг/м³; g - ускорение свободного падения, м/с².

Произведение есть избыточное давление (по отношению к 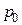), или давление столба жидкости над точкой А. Если внешнее давление равно атмос-ферному, то избыточное давление назы-вается манометрическим.

Из рис.2.1 видно, что h = z₀ - z. Тогда (2.1) можно преобразовать:

,

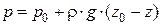. (2.2)

В (2.2) величина называется пьезометрической высотой. При нулевом значении внешнего давления она соответствует высоте столба жидкости над данной точкой. Из последнего соотношения следует, что сумма пьезометрической и геометрической высот для любой точки неподвижной жидкости является величиной постоянной и определяется внешним давлением и положением поверхности жидкости. Данная сумма имеет свое название - гидростатический напор: H_c = + z. Величина гидростатического напора выражается в метрах. Произведение mgH_c, где m - масса какого-либо элемента жидкости, характеризует потенциальную энергию этого элемента, равную механической работе, которую он может совершить при переходе на плоскость сравнения. В соответствии с (2.2) потенциальная энергия для любых точек неподвижной жидкости одинакова.

Жидкость в состоянии движения. Состояние жидкости, находящейся в движении, определяется давлениями и скоростями во всех точках потока. Картина скоростей в каждый данный момент времени и в пространстве называется полем скоростей, а картина давлений - полем давлений.

Различают движение установившееся и неустановившееся. Если скорость и давление в каждой точке пространства, заполненного движущейся жидкостью, не изменяются во времени, движение называется установившимся, то есть скорость v и давление p являются только функциями координат:

v = v(x,y,z),

p = p(x,y,z).

Установившееся движение может быть равномерным и неравномерным. Равномерное движение соответствует случаю, когда на рассматриваемом участке потока сохраняются постоянными площадь поперечного сечения потока 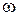и его скорость v. Если данные условия не соблюдаются, то движение будет неравномерным.

Для неустановившегося движения поля скоростей и давлений в каждой точке потока изменяются со временем t:

v = v(x,y,z,t),

p = p(x,y,z,t).

Потоки жидкости часто характеризуют усредненными по сечению параметрами. При этом пользуются следующими понятиями:

площадь живого сечения 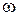, м², - это площадь поперечного сечения потока жидкости;

расход потока Q, м³/с, - объем жидкости, протекающей через поперечное сечение потока в единицу времени;

сток потока W, м³, - суммарный объем жидкости, прошедший через поперечное сечение потока за какое-либо время t (W =Q t );

средняя скорость потока v, м/с, определяется как v = Q/ .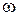

Из определения средней скорости потока следует, что

.

Если поток жидкости не имеет дополнительных каналов притока или потерь, то расход жидкости в каждом его сечении постоянен, то есть

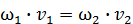.(2.3)

Индексы 1 и 2 соответствуют номеру сечения потока. Уравнение (2.3) называется уравнением неразрывности потока и является первым основным уравнением гидродинамики. Из него следует, что

,

то есть средние скорости в поперечных сечениях обратно пропорциональны площадям этих сечений.

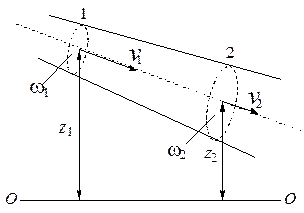Рис. 2.2. Схема потока жидкости и его характеристики в сечениях 1 и 2

Вторым основным уравнением гидродинамики является уравнение, устанавливающее зависимость между скоростью и давлением в различных сечениях потока жидкости.

Рассмотрим поток идеальной жидкости в потенциальном поле Земли (рис. 2.2). Для идеальной жидкости диссипативные потери энергии при движении отсутствуют. В связи с этим полная механическая энергия какой-либо выделенной части жидкости потока, равная сумме потенциальной и кинетической энергий (Э = mgH_c + mv²/2), в каждом сечении потока сохраняется:

Э = mgH_с1 + mv₁²/2 = mgH_c2 + mv₂²/2. (2.4)

Здесь m - масса выделенной части жидкости; g - ускорение свободного падения. Разделив выражение (2.4) на mg и учитывая определение H_c, получим

Э/mg = . (2.5)

Это уравнение носит название уравнения Бернулли. Здесь v₁²/2g и v₂²/2g - удельные кинетические энергии жидкости (скоростные напоры) в сече-ниях 1 и 2. Удельная энергия потока Э/mg (полная механическая энергия элемента жидкости потока весом 1 Н) имеет размерность длины (м), обозначается H_g и называется гидродинамическим напором. В соответствии с (2.5)

. (2.6)

Из уравнения Бернулли следует, что гидродинамический напор в любом сечении потока жидкости постоянен. Это уравнение выражает для движущейся жидкости закон сохранения механической энергии и устанавливает важную зависимость между v, p и z.

Уравнение Бернулли, записанное в форме (2.5), справедливо лишь для идеальной жидкости и при отсутствии потерь на трение. Для реальных потоков с учетом неравномерности распределения скоростей по площади живого сечения и потерь напора H_g, связанных с работой сил трения, уравнение Бернулли записывается следующим образом:

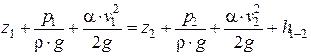, (2.7)

где 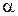- коэффициент Кориолиса (обычно 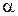=1,045 - 1,1); - величина потери гидродинамического напора на участке между сечениями 1 и 2.