ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ И ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ

Под влиянием электрического поля связанные электрические заряды диэлектрика смещаются в направлении действующих на них сил и тем больше, чем выше напряженность поля. При снятии элек­трического поля заряды возвращаются в прежнее состояние. В по­лярных диэлектриках, содержащих дипольные молекулы, воздей­ствие электрического поля вызывает еще и ориентацию диполей в направлении поля; при отсутствии поля диполи дезориентируются вследствие теплового движения.

Большинство диэлектриков характеризуется линейной зависи­мостью электрического смещения от напряженности электрического поля, созданного в диэлектрике. Особую группу составляют ди­электрики, в которых с изменением напряженности поля смещение меняется нелинейно, обнаруживая насыщение при некотором зна­чении напряженности поля. Такие диэлектрики называются сегнетоэлектриками.

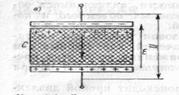
Рис.1.

Любой диэлектрик с нанесенными на него электродами, вклю­чённый в электрическую цепь, может рассматриваться как конден­сатор определенной емкости. (рис. 1).

Заряд конденсатора, как известно, равен

Q = CU, (1)

где С—емкость конденсатора; U—приложенное напряжение.

Заряд Q при заданном значении приложенного напряжения сла­гается из заряда Q₀, который присутствовал бы на электродах, если бы их разделял вакуум, и заряда Q_д, который обусловлен по­ляризацией диэлектрика, фактически разделяющего электроды:

Q = Q_o + Q_д. (2)

Одной из важнейших характеристик диэлектрика является его относительная диэлектрическая проницаемость 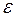. Эта величина представляет собой отношение заряда Q, полученного некотором напряжении на конденсаторе, содержащем данный диэлектрик, к заряду Q₀, который можно было бы получить в конденсаторе тех же размеров и при том же напряжении, если бы между электродами находился вакуум:

, (3)

Из (3) следует, что относительная диэлектрическая проницаемость любого вещества больше единицы и равна единице только для вакуума.

Для характе­ристики качества диэлектриков используется именно эта величина, причем слово «относительная» для краткости опускается.

Соотношение (1), приведенное выше, может быть представлено в виде

, (4)

где С₀ —емкость, которую имел бы данный конденсатор, если бы его электроды разделял вакуум.

Из формулы (4) следует, что диэлектрическую проницаемость вещества можно определить как отношение емкости конденсатора с данным диэлектриком к емкости конденсатора тех же размеров, диэлектриком которого является вакуум.