Определение максимально допустимой нагрузки.
При небольшой толщине соединяемых пластин и значительных нагрузках между поверхностью соединительных деталей и стенками отверстий возникает взаимное давление, в результате стенки отверстий обминаются.
Давление, возникающее между поверхностью соединительных деталей и отверстием – напряжение смятия σсм.
Задача №1

 Два листа соединены заклепкой. На соединение действует сила Р = 5 кН. Определить, достаточна ли прочность заклепки, если ее диаметр d = 10 мм, а [τср] = 80 Н/мм2
Два листа соединены заклепкой. На соединение действует сила Р = 5 кН. Определить, достаточна ли прочность заклепки, если ее диаметр d = 10 мм, а [τср] = 80 Н/мм2
 P
P
P
D
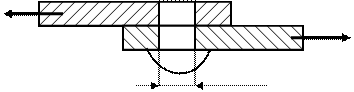
1. Определение внешних сил, действующих на заклепку.
Через листы на заклепку передается действие сил Р, они действуют в параллельных плоскостях на очень малом расстоянии друг от друга и нап-равлены в противоположные стороны.
2 Определение внутренних сил, действующих в заклепке.
Нетрудно заметить, что единственным сечением заклепки, в котором возможна деформация (исключая деформацию смятия на боковых поверх-ностях), является сечение, совпадающее со стыком листов Применив метод сечения, выясняем, что равнодействующая внутренних сил Q равна Р, а сами силы ориентированы так, что появятся касательные напряжения сдвига.
3. Проверка прочности заклепки. Прочность заклепки будет обеспечена, если возникающие в ней действительные напряжения сдвига не превысят допуска-емых.
Действительные напряжения 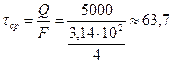 Н/мм2
Н/мм2
Так как  τср<[τср], то прочность обеспечена.
τср<[τср], то прочность обеспечена.
3 а д а ч а №2.
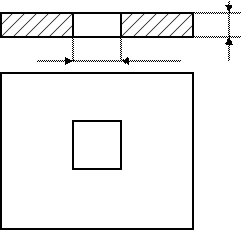
В стальном листе толщиной δ = 10 мм пробили на прессе квадратное отвер-стие со стороной а = 20 мм Определить силу, которая потребовалась для пробивания отверстия, если предел прочности при срезе τПЧ= 400 Н/мм3.
 δ
δ
а
1 Общая схема решения.
При пробивании отверстия произошло разрушение материала листа по четы-рем поверхностям, следовательно, действительные напряжения при этом достигли напряжений предела прочности. Вполне очевидно, что при этом происходила деформация сдвига (среза). Таким образом, требуется опре-делить внутреннюю и равную ей внешнюю силы по известным напряжениям и размерам, позволяющим подсчитать общую площадь деформируемых сечений.
2. Определение общей площади деформируемых сечений.
Эта площадь представляет собой площадь четырех прямоугольников с размерами 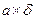 .
.
Таким образом F=4a∙δ=4∙20∙10= 800 мм2
3 Определение силы, потребной для пробивания отверстий.
Формула для расчета напряжений при сдвиге (срезе)
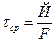 , но так как Q=P и τср=τПЧ, то P=τПЧ∙F=400∙800=320000Н. Р=320кН
, но так как Q=P и τср=τПЧ, то P=τПЧ∙F=400∙800=320000Н. Р=320кН
КРУЧЕНИЕ
Вид деформации при котором возникает один внутренний силовой фактор-крутящий момент, называется кручением.

c1
b c
d1
a d Mвр
γ-угол сдвига
Вал- стержень, работающий на кручение
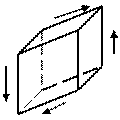 τ τ
τ τ
-Закон парности касательных напряжений
τ
τ
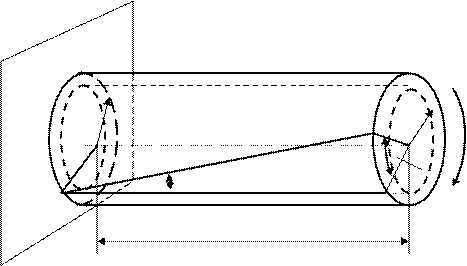
Деформация чистого сдвига рассматривается на примере кручения тонкостенной трубы. При чистом сдвиге возникают только касательные напряжения.
Закон Гука при кручении
В пределах упругих деформаций возникают касательные напряжения, которые прямо пропорциональны углу сдвига.
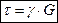
G-модуль сдвига
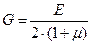 ; для стали Ст3 - G=8∙104МПа
; для стали Ст3 - G=8∙104МПа
Эпюра крутящих моментов- диаграмма крутящих моментов по длине вала.
 |
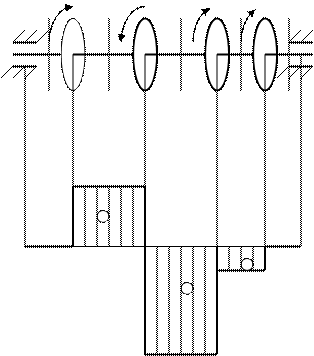 I M1 II M2 III M2 IV M4 V M1=60кНм
I M1 II M2 III M2 IV M4 V M1=60кНм
М2=20кНм
М3=35кНм
М4= 5кНм
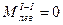
I II III IV V 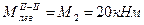
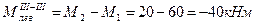
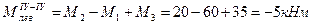
20 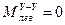
 |
-5 Мкр
-40
Крутящий момент в сечении численно равен алгебраической сумме всех внешних сил расположенных в плоскости ┴оси вала относительно точки центра тяжести сечения и находящийся по одну сторону от рассматриваемого сечения.
Правило знаков
Крутящий момент в сечении а-а считается положительным, когда внешний момент вращаем отсеченную часть против часовой стрелки, если смотреть на отсеченную часть со стороны сечения. Если же внешний момент вращает отсеченную часть по часовой стрелке (при взгляде со стороны сечения), то крутящий момент в сечении будем считать отрицательным.
М М М М
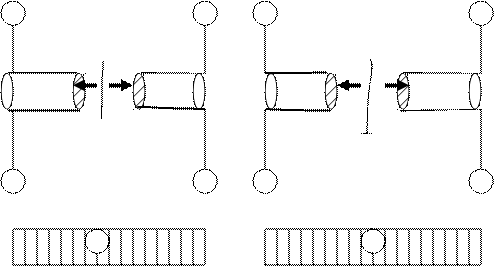 ● ┼ ┼ ●
● ┼ ┼ ●
Мкр>0 Мкр<0
а а
а а
┼ ● ● ┼
Мкр ┼ ▬ Мкр
Условия прочности и жесткости при кручении
I II
r
N1 C1 δ
O O1
φ Mвр
K γ N C
L
Угол сдвига для элемента, лежащего на поверхности стержня, равен отношению отрезка NN1 к длине элемента dz
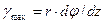 (1)
(1)
Выделяя мысленно из рассматриваемой части бруса цилиндр произвольного радиуса δ и повторяя те же рассуждения, получим угол сдвига для элемента, отстоящего на расстоянии δ от оси стержня
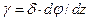 (2)
(2)
На основании закона Гука при сдвиге имеем

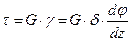 (3)
(3)
Как видим, при кручении деформации сдвига и касательные напряжения прямо пропорциональны расстоянию от центра тяжести сечения.
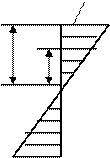
Эпюра касательных напряжений
 τ max
τ max
 D
D
D1
φ r δ τ
C1 C
B1 B
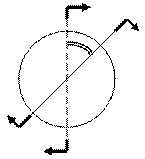
В центре тяжести касательные напряжения равны нулю. Наибольшие касательные напряжения будут в точках сечения, расположенных у поверхности сечения.
Равнодействующий момент касательных напряжений в сечении:
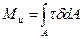 (4)
(4)
где 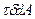 -элементарный крутящий момент внутренних сил, действующих по площадке dA.
-элементарный крутящий момент внутренних сил, действующих по площадке dA.
Подставив в (4) значение напряжений из формулы (3), получим
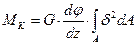 (5)
(5)
Имея в виду, что
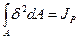 , (6)
, (6)
Где 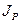 - полярный момент инерции сечения, получим
- полярный момент инерции сечения, получим

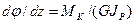 (7)
(7)
Подставляя значение 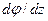 в формулу (3), имеем
в формулу (3), имеем
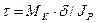 (8)
(8)
В частном случае, когда на стержень действует один внешний скручивающий момент М, из условия равновесия отсеченной части стержня получим МК=М.
Таким образом, окончательная формула для определения касательных напряжений при кручении имеет вид
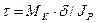 (9)
(9)
Эта формула показывает, что, в точках, одинаково удаленных от центра сечения, напряжения τ одинаковы. Наибольшие напряжения в точках у контура сечения равных
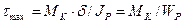 , (10)
, (10)
Где
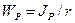 (11)
(11)
Геометрическая характеристика WP называется полярным моментом сопротивления или моментом сопротивления при кручении.
Для круглого сплошного сечения 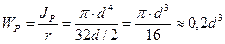 .
.
Для кольцевого сечения 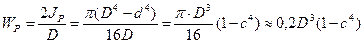
Где 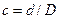
Дата добавления: 2020-07-18; просмотров: 530;











