Кинематический анализ манипулятора

Прямая задача о положении манипуляторов позволяет определить
координаты схвата или его траекторию движения, а также ориентацию схвата вдоль всей траектории. Прямая задача о скоростях состоит в определении абсолютных линейных скоростей точек звеньев манипулятора и угловых скоростей звеньев при заданных законах изменения обобщенных координат. Для кинематического исследования пространственных кинематических цепей существуют различные методы. При исследовании кинематики роботов рациональнее использовать матричный метод.

Рассмотрим манипулятор с тремя степенями свободы. Функцией положения точки D схвата (рис. 3.10) будет зависимость ее радиуса-вектора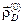

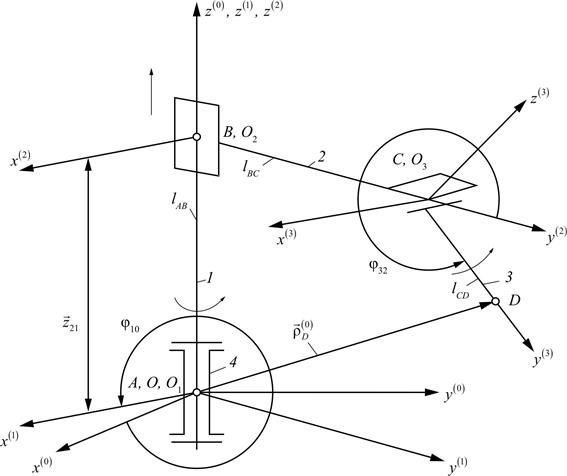
Рис. 3.10. Кинематический анализ манипулятора

от обобщенных координат и постоянных длин звеньев l_ВС и l_DC. Данный механизм с незамкнутой кинематической цепью является статически определимым, без избыточных связей (q = 0), поскольку он собирается без натягов. В механизме три одноподвижные пары: две из них вращательные (А, С) и одна поступательная (В). Обобщенных координат три: j₁₀ – угол поворота звена 1 относительно стойки 4; z₂₁ – линейное перемещение звена 2 относительно звена 1; j₃₂ – угол поворота звена 3 относительно звена 2. Число степеней свободы W = 3 подтверждается и по формуле Малышева:

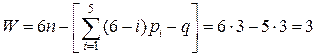Система координат O₁x⁽¹⁾y⁽¹⁾z⁽¹⁾связана со звеном 1, вращающимся вокруг оси z⁽¹⁾, система O₂x⁽²⁾y⁽²⁾z⁽²⁾ – со звеном 2, движущимся прямолинейно относительно звена 1, а система О₃х⁽³⁾у⁽³⁾z³ – со звеном 3, вращающимся вокруг оси z⁽³⁾. Оси x⁽¹⁾, x⁽²⁾, x⁽³⁾параллельны.

Функция положения в матричной форме имеет такой вид:

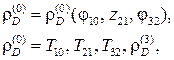
¨ где

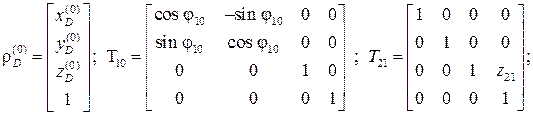
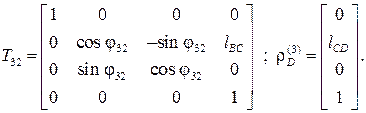
Последовательным умножением матрицы приводят к равенству

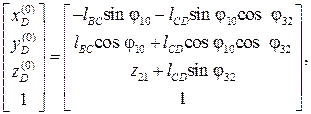
следовательно, искомые координаты точки D в неподвижной системе Ох⁽⁰⁾y⁽⁰⁾z⁽⁰⁾будут следующими:

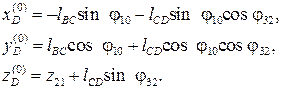
С помощью зависимостей, имея заданный диапазон изменения координат точкиD, можно подобрать нужные значения длин звеньев l_ВС, l_CD и диапазоны изменения обобщенных координат j₁₀, z₂₁ и j₃₂.

Скорость движения схвата и отдельных звеньев манипулятора определяется не только характером рабочего процесса, но и условиями безопасности для обслуживающего персонала. Если зависимости обобщенных координат от времени известны, то скорости можно найти дифференцированием по времени функции положения. Например, для рассмотренного манипулятора с тремя степенями свободы при заданных зависимостях j₁₀(t), z₂₁(t) и j₃₂(t) проекции вектора скорости точки D схвата на оси координат получим, дифференцируя выражения:

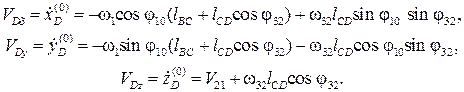
Величину и направление вектора скорости точки D найдем по формулам:

, ,

, .

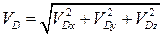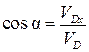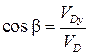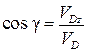¨ где a, b, g – направляющие углы вектора скорости.

3.8. Графоаналитический метод кинематического
исследования рычажных механизмов

Графоаналитический метод, или метод планов, основан на элементах векторной алгебры. При кинематическом исследовании составляются векторные уравнения для скоростей или ускорений механизма в данном положении. Полученные уравнения решаются графически в порядке присоединения структурных групп к ведущему звену и к стойке. Метод планов применяют тогда, когда имеется схема механизма в данном положении. Рассмотрим примеры применения графоаналитического метода.

3.8.1. Определение предельных положений механизма
(графический метод)

Решение задачи начинают с определения предельных положений механизма, когда рабочий орган механизма занимает крайнее положение. Рассмотрим способы, пользуясь которыми можно в зависимости от типа механизма найти предельные положения.

Для шарнирного четырёхзвенника (рис. 3.11, а, б) предельные положения коромысла 3 будут тогда, когда кривошип 1 и шатун 2 располагаются на одной прямой. Из точки А в масштабе радиуса кривошипа, а из точки D радиусом коромысла проводим окружности. Затем из А проводим засечки длинами АВ+ВС и ВС–АВ до пересечения с траекторией коромысла в точках С₁и С₂. Полученные точки С₁и С₂соединяем с точкой А отрезками, пересекающими окружность кривошипа в точках В₁и В₂.Положение механизма, соответствующие схемам AB₁C₁D и AB₂C₂D – предельные (рис. 3.11, б).

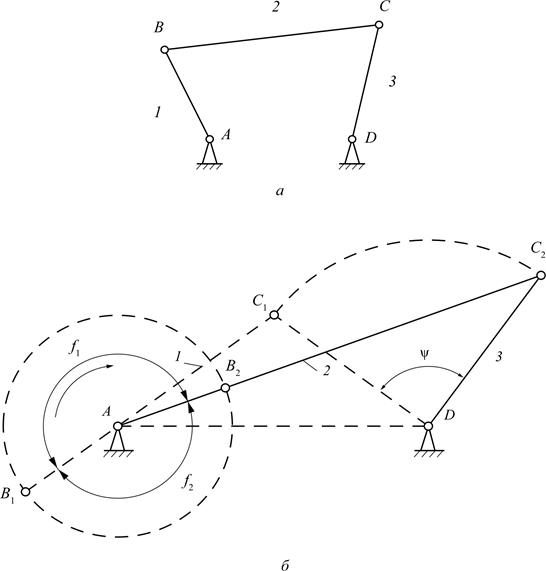
Pис. 3.11. Шарнирный четырёхзвенник:
а – кинематическая схема шарнирного четырёхзвенника;
б – крайние положения шарнирного четырехзвенника

Методика определения крайних положений для кривошипно-ползунного механизма (рис. 3.12) аналогична той, которая рассмотрена выше.

Для механизма с качающейся кулисой определение предельных положений начинают с построения окружности кривошипа 1 с центром в точке А.Затем проводятся две касательные к этой окружности из точки D – центра качения кулисы 3.Эти прямые и характеризуют схемы AB₁D и AB₂D механизма, соответствующие двум крайним положениям (рис. 3.13).

Рис. 3.12. Кривошипно-ползунный механизм:
а – кинематическая схема кривошипно-ползунного механизма;
б – крайние положения кривошипно-ползунного механизма

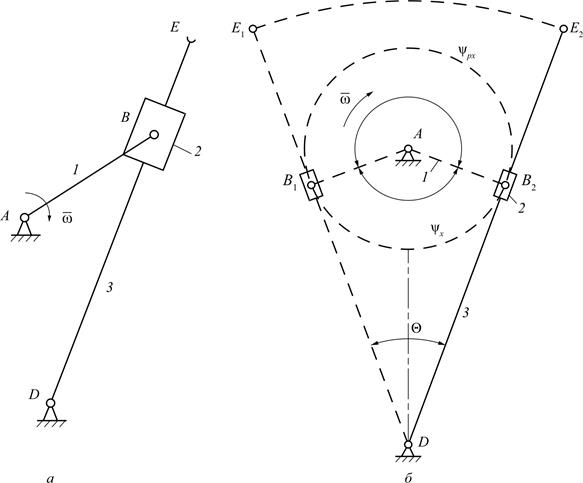
Рис. 3.13.Кулисный механизм: а – кинематическая схема механизма;
б – крайние положения механизма

Для более сложных стержневых механизмов крайние положения определяют исходя из конкретной схемы с учётом способов, изложенных выше.

3.8.2. Построение плана положений механизма

Построение плана положений механизма проводится в определённом масштабе μ_l. Масштаб схемы характеризует отношение длины (м) входного звена к отрезку плана положений (мм), соответствующего этому звену. Например, μ_l = ℓ_ОА / (ОА), м/мм.

Рекомендуется масштаб выбирать простым числом, чтобы с ним удобно было проводить вычисления. Выбрав масштаб, определяют длины отрезков схемы, соответствующие остальным звеньям. Например, ВС = ℓ_ВС /μ_l,мм, CD = ℓ_cd / μ_l, мм и т.д.

После выбора масштаба строятся крайние положения механизма, одно из которых принимается за начальное, соответствующее началу рабочего хода. Таким образом, за нулевое положение (начало отсчёта) принимается положение кривошипа, соответствующее начальному.

Построение всех текущих положений механизма ведётся в порядке присоединения структурных групп методом засечек в соответствии с направлением движения ведущего звена. На рис. 3.14 изображена схема кулисного механизма в 12 положениях в масштабе μ_l.

Системой координат S–f строим систему координат V₀f c тем же расположением положений f₁, f₂ и т.д. На оси f левее O откладывается отрезок H₁произвольной величины. При этом следует учесть, что чем больше H₁, тем больше величины ординат диаграммы Vf₁= ĩ (f₁). Из точки O₁ проводим лучи O₁ – 1', O₁ – 2', O₁ – 3' и т.д., параллельные хордам 1 т.д. Проведённые лучи отсекают на оси ординат отрезки O – 1', O – 2', O – 3' и т.д., величины которых откладываются по вертикали из середин отрезков 0–1, 1–2, 2–3 и т.д. оси Of. Соединив полученные точки плавной кривой, получают график скорости точки (рис. 3.15, б). Масштаб скорости и его аналога

μ_V = (μ_S/H₁∙ μ_f) ω₁= μ_S/μ_t ∙H₁;

μ_Vf = μ_S / H₁∙μ_f_.

Имея график Vf = V (f), можно найти значение скорости в любом положении кривошипа. Например, для 5-го положения

V_E₅= μ_V × (y₅).

Аналогичным образом строится график ускорения точки (рис. 3.15, в). В случае прямолинейного движения точки – это полное ускорение, иначе – тангенциальное. Масштаб ускорения для диаграммы:

μ_a = μ_V /μ_t ∙H₂= (μ_V /μ_f ∙H₂) ώ₁², мс^–2/мм.

На рис. 3.15 показана диаграмма движения точки Е выходного звена:

а) перемещение и путь: S = f (f);

б) скорость точки Е: V = f (t);

в) ускорение точки Е: a = f (t).

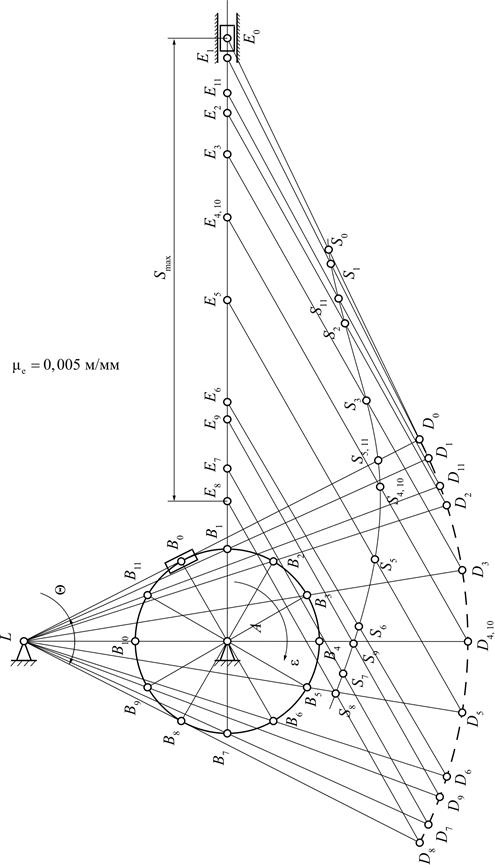
Рис. 3.14. Планы положений кривошипно-кулисного механизма

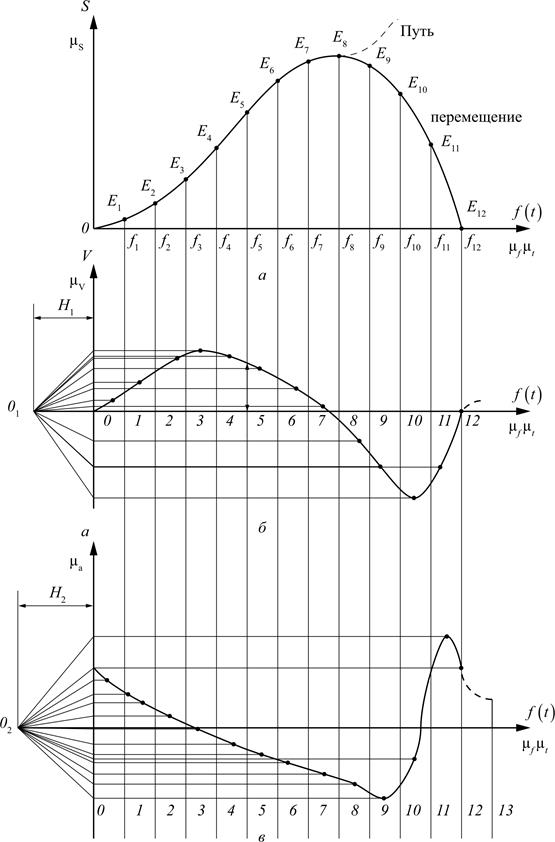
Рис. 3.15. Диаграммы движения выходного звена:
a – график изменения перемещений и пути звена; б – график
изменения скорости звена; в – график изменения ускорений звена

3.9. Примеры расчёта рычажных механизмов
графоаналитическим методом кинематического
исследования

3.9.1. Механизм шарнирного четырехзвенника ABCD

Структурная формула 1→2₁.

Исходные данные: ℓ_AD= ℓ₀; ℓ_AB= ℓ₁; ℓ_BC= ℓ₂; ℓ_CD= ℓ₃.

Схема механизма в данном положении представлена на рис. 3.16.

Угловая скорость кривошипа может быть найдена по формуле

.

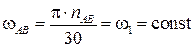Скорость точки В: 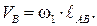Вектор скорости V_B перпендикулярен звену АВ схемы и направлен в сторону вращения кривошипа АВ.

На чертеже выбираем произвольно точку р – полюс. V_p = 0. Из т. р проводим вектор рb,изображающий скорость точки В (рис. 3.16, а). Длина отрезка рb выбирается произвольно, но такой, чтобы масштаб плана скоростей 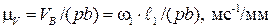, выражался простым числом.

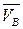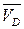Затем для структурной группы 2₁записываем векторные уравнения скоростей. Скорости концевых элементов группы и = 0 известны:

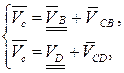(3.83)

где 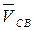– вектор относительной скорости точки С в ее движении относительно точки В; 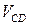– вектор относительной скорости точки С вокруг D.

Величины этих векторов неизвестны. По направлению 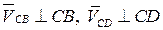. Исходя из этого, согласно первому уравнению системы (3.83), из т. b проводим луч соответственно _┴звену CB схемы, а согласно второму уравнению (3.83) из т. p – луч _┴ СD. Пересечение лучей дает точку С – конец вектора 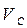. Т. С соединяем сполюсом p (рис. 3.16, а).

.

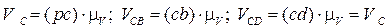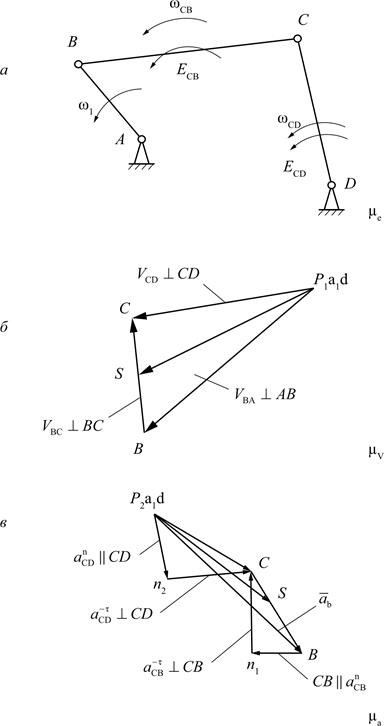
Рис. 3.16. Кинематическое исследование механизма шарнирного
четырёхзвенника: а – схема механизма; б – план ускорений; в – план скоростей

Положение точки S, соответствующей точке S схемы, определяем на плане скоростей из пропорции 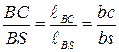по свойству подобия. Соединив S с полюсом p, получим величину и направления скорости точки S: .

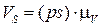Угловая скорость звеньев CB, СD:

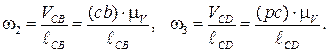
Направление угловых скоростей ω₂и ω₃определяется прикладыванием векторов 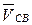и 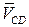соответственно в точках С схемы (рис. 3.16, а). Угловая скорость ω₂ вращает звено СВ относительно точки В против часовой стрелки, а угловая скорость ω₃вращает звено СD относительно точки D,также против часовой стрелки.

Построение плана ускорений начинаем с определения ускорения точке В при равномерном вращении .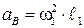

Вектор 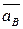направлен паралельно звену АВ к центру вращения – точки А. На чертеже выбираем точку P₂ – полюс. 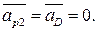Из т. P₂ проводим вектор 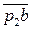, изображающий 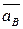(см. рис. 3.16). Длина отрезка (p₂b) выбирается произвольной, но такой, чтобы масштаб плана ускорений

,

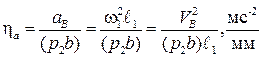¨ выражался простым числом.

Векторное уравнение ускорений для структурной группы 2₁:

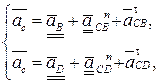(3.84)

где 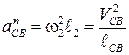– нормальное ускорение точки С относительно т. В, направленное вдоль СВ от С к В;

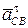– тангенциальное ускорение точки С относительно В, направленное перпендикулярно СВ;

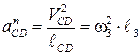– нормальное ускорение точки С относительно точки D, направленное вдоль звена CD от C к D;

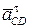– тангенциальное ускорение точки С относительно т. D, направленное перпендикулярно звену CD.

Вектору 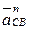соответствует отрезок 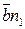плана, длина которого 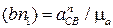. Вектор 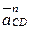соответствует вектору 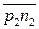плана с длиной 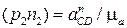(рис. 3.16, б).

С учетом уравнений системы (3.84), значений 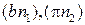и их направлений достраиваем план ускорений. Соединив полученную точку С с полюсом p₂, получим вектор 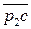, соответствующий 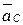(рис. 3.16, б).

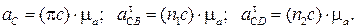
Ускорение точки S находим, соединив т. c и b:

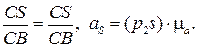
Угловые ускорения звеньев 2 и 3:

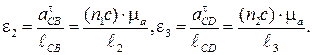
Направление векторов 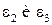определяется установкой векторов 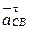и 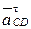в точку С схемы по способу, рассмотренному выше для угловых скоростей (рис. 3.16).

3.9.2. Кривошипно-ползунный механизм АВС

Структурная формула 1→2₂.

Исходные данные: ℓ_AB= ℓ₁; ℓ_BC= ℓ₂; ℓ_OA= ℓ₀:n_ab.

.

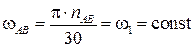Скорость точки В: 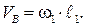Вектор скорости V_B перпендикулярен звену АВ схемы и направлен в сторону вращения кривошипа АВ.

По аналогии с примером (см. рис. 3.16, а) строим вектор .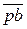

Масштаб:

.

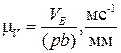Далее для структурной группы 2₂составляем векторные уравнения скоростей.

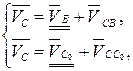(3.85)

где 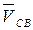– вектор относительной скорости точки С вокруг точки В, ;

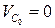– скорость неподвижной точки направляющей х–х, совпадающей в данный момент с точкой С;

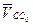– вектор относительной скорости точки С в движении ее относительно направляющей, 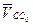– параллельный х–х,

поэтому в соответствии с 1-м уравнением (3.85), из т. b проводим луч соответственно _┴звену CB схемы, а в соответствии со 2-м уравнением (3.85) из С_Х проводим луч // х–х. На пересечении получается точка С, которая соединяется с полюсом р (рис. 3.17, а). В результате получают:

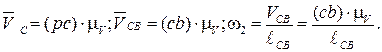
Направление 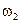определяется по правилу, рассмотренному в примере (рис. 3.16, а). Скорость точки S находим, используя подобие из пропорции 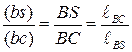. Соединив полюс p с S,получим абсолютную скорость точки S: 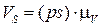(рис. 3.17, а).

Подробнее остановимся на определении скорости точки К (рис. 3.17). Для этого на плане скоростей строим треугольник ∆АВС~∆ВКС схемы. При этом должна соблюдаться идентичность направлений обхода контура вкс как на плане, так и на схеме механизма:

.

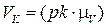Переходим к построению плана ускорений. 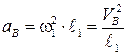. Вектор 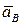направлен по звену АВ от В к А. Отрезок (р₁b) по аналогии с предыдущим примером (рис. 6, а) откладываем от полюса р₁ (рис. 3.16, б). Масштаб построения 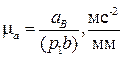, где длина отрезка (р₁b) в мм выбирается произвольной, но удобной для дальнейших расчетов.

Векторное уравнение для ускорений группы 2₁:

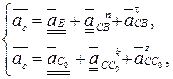(3.86)

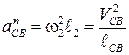– нормальное ускорение точки С относительно т. В, направленное вдоль СВ от С к В;

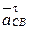– тангенциальное ускорение точки С относительно В, направленное перпендикулярно СВ;

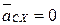– ускорение точки неподвижной направляющей, совпадающей в данный момент с точкой С;

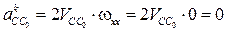– ускорение Кориолиса в движении точки С относительно т. С_Х и вместе с ней. Вращательное движение направляющей х–х отсутствует ;

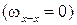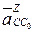– относительное (релятивное) ускорение в движении точки 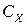, направлено вдоль направляющей х–х.

соответствует отрезок 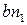, длина которого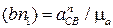

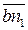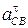С учетом 1-го уравнения системы (3.86), из точки b плана проводим // ВС (от С к В), затем из т.n₁ проводится луч (направление ). По 2-му уравнению системы (3.86) 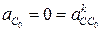, то из точки p₂ проводим луч // х–х (направление 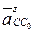). На пересечении лучей получается точка С, которая соответствует концу вектора 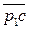, характеризующего 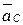(рис. 7, б). По величине 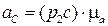далее:

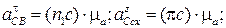
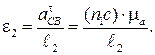
Направление углового ускорения звена 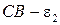по правилу, приведенному на рис. 3.17, а.

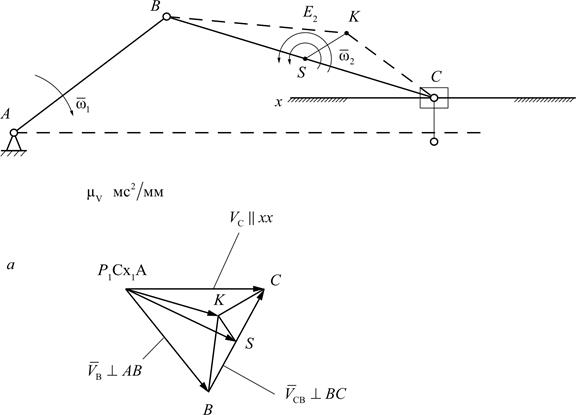
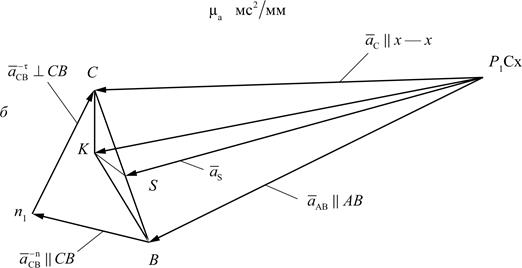
Рис. 3.17. Планы скоростей (а) и ускорений (б)
для кривошипно-ползунного механизма

Ускорения точек S и К определяется из подобия по пропорции:

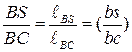
по тому же принципу, что и при построении плана скоростей:

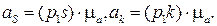
3.9.3. Кулисный механизм АВС

Структурная формула 1 → .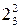

Исходные данные: ℓ_AB= ℓ₁; ℓ_А_C= ℓ₀; ℓ_CD= ℓ₃.

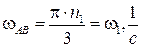
Для данного механизма (рис. 3.18) рассматриваются точки В₁, В₂, В₃,принадлежащие соответственно концу кривошипа, камню кулисы, самой кулисе и совпадающие в заданный момент времен:

.

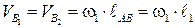Вектор 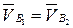перпендикулярен АВ и направлен в сторону вращения этого звена. Из полюса р проводим вектор 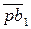(рис. 3.18, а), соответствующий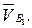

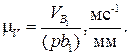
Для структурной группы 2₃векторное уравнение скоростей имеет вид

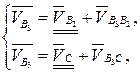(3.87)

где 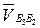– вектор относительной скорости точки B₃ кулисы в движении относительно точки В₂ камня кулисы, 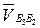// В₃С;

;

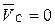т. С.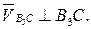

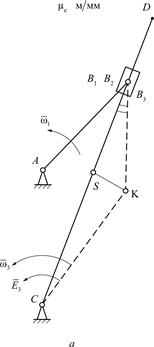
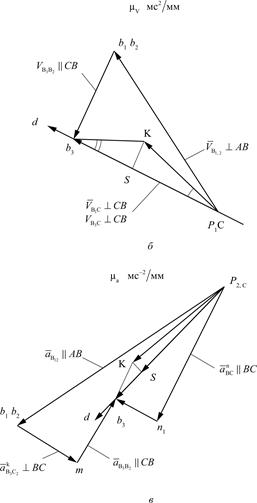
Рис. 3.18. Кинематическое исследование кулисного механизма:
а – схема механизма; б – план механизма; в – план ускорений

В соответствии с первым уравнением (3.87), из т. b₂ плана скоростей проводим луч, параллельный кулисе В₃С, а по второму уравнению системы (3.87) из полюса р проводим луч, перпендикулярный ВС (т. р и С совпадают, т.к. ).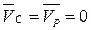

На пересечении лучей находим точку b₃, которая является концом вектора ,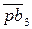

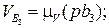
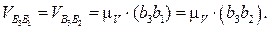
Скорость точки D определяем из подобия:

.

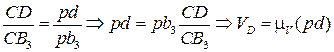Скорости точек S и К находятся по аналогии с примером

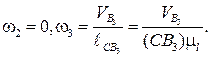
Направление 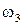(рис. 3.18, а) находится по ранее введенному правилу. Полный план скоростей представлен рис. 3.18, а.

Для плана ускорений .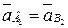

По величине .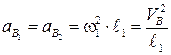

Из полюса р₂плана ускорений параллельно АВ от схемы В к А откладываем вектор 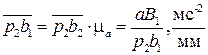, (рис. 3.18, б).

Для структурной группы 2₃векторные уравнения для ускорений запишутся следующим образом:

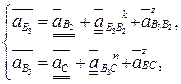(3.88)

где 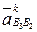– ускорение Кориолиса в движении точки В₃ относительно т. В₂ и вместе с ней;

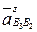– относительное ускорение точки В₃ вокруг т. С, направленное вдоль СВ от В к С;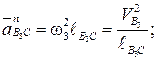

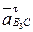– тангенциальное ускорение точки В₃ относительно т. С, направленное перпендикулярно ВС.

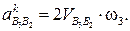
Ему соответствует вектор 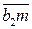, длина которого в мм чертежа 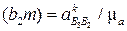. Направление этого вектора определяется путем поворота на 90° в направлении 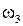относительной скорости 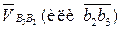из плана скоростей (рис. 3.18, а). В соответствии с первым уравнением системы (3.88) откладывается от точки b₂, а затем из т. m проводим луч // В₃С. По второму уравнению из т. С плана ускорений откладываем вектор 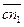параллельно ВС,направленный от В к С.

.

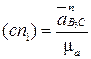Затем из т. n₁ перпендикулярно ВС строится луч, соответствующий направлению 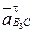. На пересечении двух лучей фиксируем точку b₃, являющуюся концом вектора 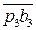– ускорения т. b₃.

Следовательно:

.

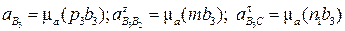Из подобия:

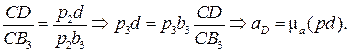
Ускорения точек S и К определяются из подобия с помощью принципа обхода контура СВК (рис. 3.18, б).

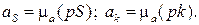
Определяем угловое ускорение 3-го звена:

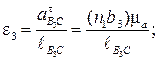
направление 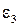показано на рис. 3.18, б.

Методики графоаналитического исследования, приведенные в примерах (рис. 3.16–3.18), применяются при кинематическом исследовании более сложных стержневых механизмов.

3.9.4. Пятизвенный стержневой механизм

Построение плана скоростей

1. V_A = V_C = V_X = 0.

2. 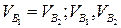(скорость перпендикулярна звену АВ),

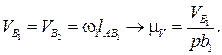
3. (скорость 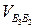параллельна звену ВС),

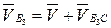(скорость 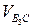перпендикулярна ВС) /

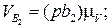
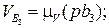
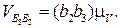
4. 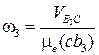. (угловая скорость звена).

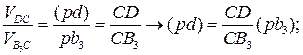
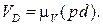
При нахождении положения точки d плана скоростей используется правило обхода контура B₃CD и b_зсd (рис. 3.19, а).

5. 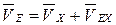(скорость V_EX параллельна х–х),

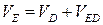(скорость V_ED перпендикулярна ED).

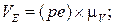
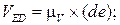
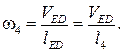
Построение плана ускорений

1. а_А= а_С= а_Х= 0.

2. 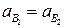; ускорения 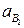, 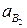параллельны звену АВ.

.

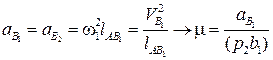3.

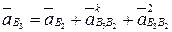
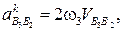
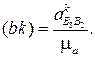
Ускорение 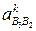параллельно звену ВС,

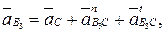
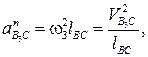
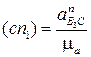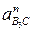, параллельно звену ВС; 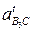перпендикулярно ВС.

Графическое построение, согласно векторным уравнениям, приводится на рис. 3.19. По результатам этих построений получаем:

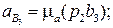
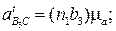
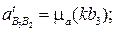
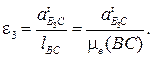
4.

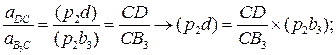
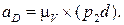
Положение точки d плана ускорений находится по правилу обхода контура B₃CD и b_зcd (рис. 3.19, б).

5.

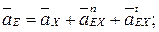
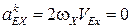( ускорение 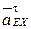параллельно неподвижной направляющей х–х).

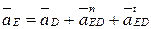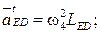
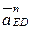( – нормальное ускорение, параллельное звену ED; 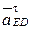– тангенцильное ускорение перпендикулярно звену ED).

По результатам графического построения векторных уравнений:

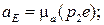
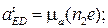
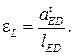
Планы скоростей и ускорений механизма в заданном положении изображены на рис. 3.19 а, б.

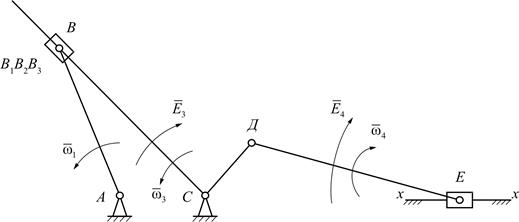
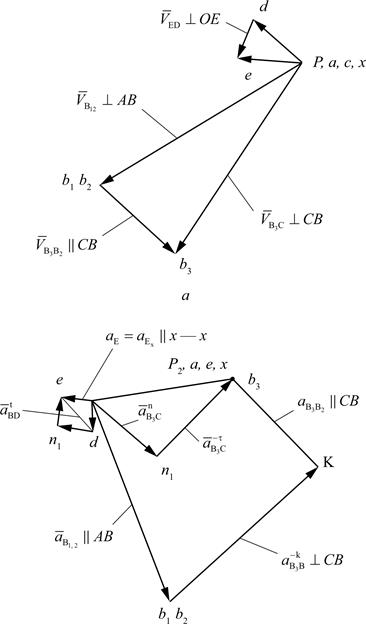
Рис. 3.19. Кинематическое исследование пятизвенного механизма:
а – схема механизма; б – план скоростей; в – план ускорения

Примечание: если по результатам расчёта значение отрезка плана меньше 2 мм, то обычно его принимают за 0, т.е. отрезок превращается в точку. Для оценки угловых движений звеньев механизма строят график изменения угловой скорости заданного звена.

Построение годографа центра масс звена

Для построения годографа скорости или ускорения какой-либо точки механизма выбирается произвольная точка 0. От этой точки откладываются векторы скоростей и ускорений рассматриваемой точки для всех К построенных положений механизма. Каждый вектор откладывается из точки в одном и том же масштабе при соблюдении его направления согласно плану скоростей или ускорений. Пример годографа скоростей точки представлен на рис. 3.20.

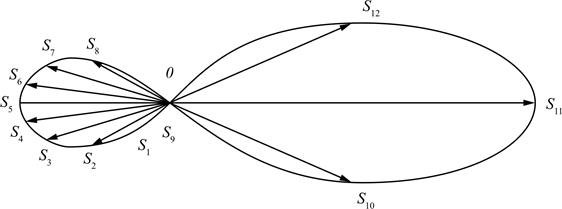
Рис. 3.20. Годограф скорости точки S

3.10. Алгоритмы кинематического анализа
рычажных механизмов

Основные положения

Развитие математических методов и ЭВМ привело к широкому использованию аналитических методов исследования кинематики механизмов.

Сущность таких методов заключается в получении для кинематических характеристик аналитических выражений, содержащих алгебраические и тригонометрические операции. Аналитические методы, в отличие от графических и графоаналитических, позволяют провести исследования кинематики эффективно, с высокой степенью точности.

Для исследования кинематики рычажных механизмов наиболее широко используется метод векторных контуров, разработанный В.А. Зиновьевым. Согласно этому методу звенья механизма представляют в виде векторов, образующих замкнутый контур. Векторные уравнения замкнутых контуров проецируют на оси координат и получают системы алгебраических уравнений для определения параметров положения звеньев механизма: перемещений и углов поворота (задача о положениях). Последовательно дифференцируя эти зависимости, составляют уравнения для определения скоростей точек и угловых скоростей звеньев (задача о скоростях), а затем и ускорений точек и угловых ускорений звеньев (задача об ускорениях), в общем случае для рычажных механизмов алгоритм кинематического анализа для всего цикла движения представлен блок-схемой на рис. 3.21.

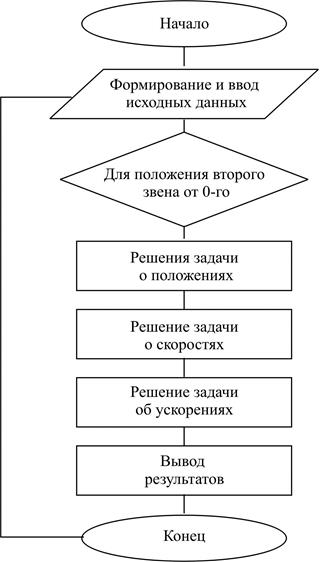
Рис. 3.21. Блок-схема алгоритма кинематического анализа

Блок-схема может быть дополнена блоком проверки существования механизма, выводами полученных результатов, печатью графиков и т.п. При проведении кинематического анализа систем известны схема рычажного механизма, размеры звеньев и закон движения входного звена. Для удобства дальнейшего изложения введем ряд допущений и обозначений:

1. Углы, образованные звеньями механизма с осью X системы координат, отсчитываются от положительного направления оси X против часовой стрелки и для К-го звена, обозначаются через φ_К.

2. Входное звено механизма обозначается индексом 1, и, например, в случае его вращательного движения оно имеет известные угловую скорость φ₁и угловое ускорение ε₁.

3. Угловая скорость и угловое ускорение К-го звена соответственно обозначаются как ω₁и ε₁, а скорость иускорение точки этого звена как V_SK и a_SK.

4. Значения угловой скорости и углового ускорения звена К выражаются через аналоги угловой скорости этого звена 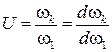и аналог углового ускорения 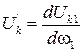следующим образом:

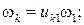
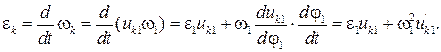
Для скорости и ускорения точки С справедливы аналогичные соотношения:

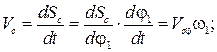
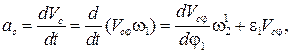
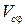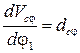где и – соответственно аналог скорости и ускорения точки С.

5. Отношение длины К-го звена к длине входящего звена обозначается через λс соответствующим индексом.

Например,

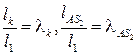и т. д.

6. Так как угол поворота К-го звена является функцией времени, то верны соотношения

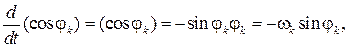
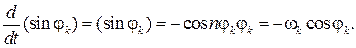
Рассмотрим ряд приемов определения кинематических характеристик некоторых механизмов, широко применяемых в машинах.

Кривошипно-ползунный механизм

Рассмотрим такой случай сборки механизма, когда при обходе по часовой стрелке сохраняется контур с последовательностью ABCDA (рис. 3.22).

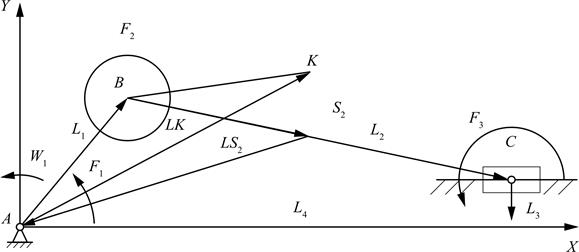
Рис. 3.22. Схема кривошипно-ползунного механизма

Задача о положениях

Уравнение замкнутости векторного контура запишется в виде

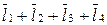= 0. (3.89)

В проекциях на оси системы координат ХАY уравнение (3.89) представляется зависимостями:

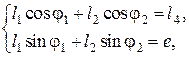(3.90)

так как φ₃= 270°, φ₄= 180°. Из второго уравнения системы (3.90) определяется угол φ₂, характеризующий положение шатуна:

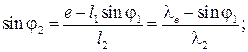(3.91)

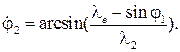(3.92)

Текущее положение ползуна (точка С) находится по формуле:

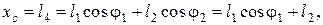
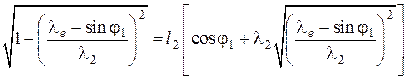. (3.93)

Максимальный ход ползуна

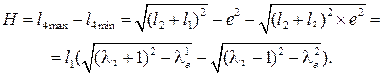
Текущее перемещение ползуна относительно одного из крайних положений, например, левого:

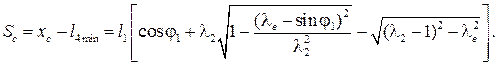
Задача о скоростях

Используя результаты решения задачи о положениях, угловую скорость шатуна можно найти дифференцированием по времени (3.91);

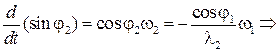
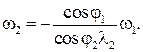
Таким образом, 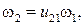(3.94)

где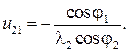

Скорость ползуна

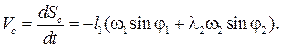(3.95)

Задача об ускорениях

Эта задачи решается путем дифференцирования первых производных, полученных для определения скоростей:

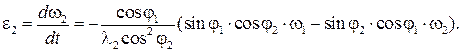(3.96)

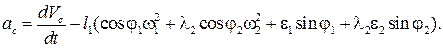(3.97)

Для определения положений центров масс звеньев (например, точка S₂ шатуна) и других точек звеньев (например, точка К) записываем векторные уравнения:

,

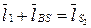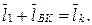(3.98)

В проекциях на оси координат перемещения этих точек в соответствии с соотношениями (3.98) будут следующими:

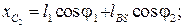
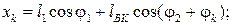(3.99)

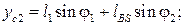
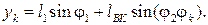
Дифференцируя соотношения (3.99), получим скорости точек S<

Дата добавления: 2020-07-18; просмотров: 735;