Дефекты кристаллической решетки
Внутренняя структура реальных кристаллов существенно отличается от рассмотренной выше модели идеального кристалла, представляющего застывшую схему, в которой неподвижные атомы образуют правильную систему точек.
В реальном идеальном кристалле вокруг каждого колеблющегося атома взаимное расположение соседних атомов отвечает их расположению в идеальном кристалле. Следовательно, искажение решетки, связанное с тепловыми колебаниями, и упругие деформации не относятся к дефектам кристаллической решетки. В реальном неидеальном кристалле из-за наличия дефектов расположения точек, вокруг которых колеблются атомы, не отвечает идеальному кристаллу.
Дефекты кристаллического строения подразделяются по геометрическому признаку на точечные (нульмерные), линейные (одномерные), поверхностные (двумерные) и объемные (трехмерные). Точечные дефекты малы во всех трех измерениях – не более нескольких атомных диаметров. К ним относятся вакансии, межузельные атомы, примесные атомы и их комплексы. Линейные дефекты малы в двух измерениях (атомного размера), в третьем – сравнимы с размерами кристалла. К линейным дефектам относятся дислокации, цепочки вакансий и межузельных атомов. Поверхностные дефекты имеют микроскопические размеры только в одном направлении. К ним относятся границы зерен, блоков, дефекты упаковки, границы доменов. Объемные дефекты имеют макроскопические размеры во всех трех измерениях.
Точечные дефекты. Точечные дефекты по своей природе обусловлены неупорядоченным размещением атомов вещества кристалла и наличием атомов примеси.
По происхождению точечные дефекты различают на тепловые, радиационные дефекты и примесные атомы, которые вводятся в кристалл целенаправленно.
Тепловые точечные дефекты обусловлены флуктуациями энергии атомов и отклонением состава кристаллов от стехиометрического. Радиационные дефекты связаны со смещением атомов из узлов решетки в процессе облучения кристалла высоко энергетическими квантами или частицами.
Точечные дефекты повышают энергию кристалла, так как на образование каждого дефекта тратится определенная энергия. Несмотря увеличение энергии кристалла при образовании точечных дефектов они могут находиться в термодинамическом равновесии с решеткой, потому что их образование приводит к росту энтропии. Эта конфигурационная энтропия определяется следующим образом
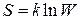 , (3.59)
, (3.59)
где 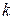 – постоянная Больцмана,
– постоянная Больцмана, 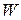 – количество возможных положений точечных дефектов по
– количество возможных положений точечных дефектов по 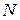 узлам решетки.
узлам решетки.
Если 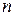 дефектов распределены между
дефектов распределены между 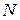 узлами решетки, то количество этих расположений будет равняться
узлами решетки, то количество этих расположений будет равняться 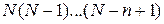 в случае, когда дефекты различаются между собой. В случае, когда дефекты одинаковы, их можно распределить
в случае, когда дефекты различаются между собой. В случае, когда дефекты одинаковы, их можно распределить 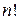 способами и в этом случае
способами и в этом случае
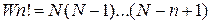 . (3.60)
. (3.60)
Преобразуем (3.60) к виду
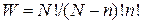 (3.61)
(3.61)
и воспользуемся приближением Стирлинга[11] для больших 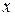 :
:  . В этом случае формула (3.59) приобретает вид
. В этом случае формула (3.59) приобретает вид
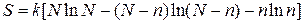 . (3.62)
. (3.62)
Изменение свободной энергии кристалла, который имеет 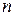 одинаковых дефектов при температуре T, будет составлять
одинаковых дефектов при температуре T, будет составлять
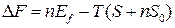 , (3.63)
, (3.63)
где  – энергия образования дефекта,
– энергия образования дефекта, 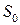 – дополнительная энтропия, которая связана с влиянием дефекта на колебания соседних атомов.
– дополнительная энтропия, которая связана с влиянием дефекта на колебания соседних атомов.
Относительное количество точечных дефектов, которые обуславливают минимальную свободную энергию, получим из условия 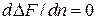 :
:
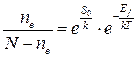 . (3.64)
. (3.64)
Самыми простыми точечными дефектами являются вакансии, которые представляют собой узлы решетки, в которых отсутствующие атомы (рис.3.8,а). Вакансии могут возникать как в процессе внутреннего «испарения» атомов, так и испарения атома с поверхности и последующей миграции образовавшейся вакансии вглубь кристалла.
Поскольку в реальности 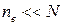 , то для вакансий уравнение (3.64) можно переписать следующим образом
, то для вакансий уравнение (3.64) можно переписать следующим образом
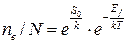 . (3.65)
. (3.65)
В ГЦК металлах 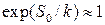 , и относительная концентрация вакансий определяется выражением
, и относительная концентрация вакансий определяется выражением 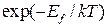 . Для
. Для 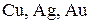 энергия образования вакансии составляет приблизительно 1 эВ, из чего следует, что при комнатной температуре относительная концентрация вакансий будет составлять
энергия образования вакансии составляет приблизительно 1 эВ, из чего следует, что при комнатной температуре относительная концентрация вакансий будет составлять 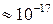 и примерно
и примерно 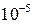 при
при  .
.
В реальных кристаллах могут образовываться также конфигурации из нескольких вакансий – бивакансии, тривакансии и т.д. Большое количество вакансий может приобретать вид симметричной объемной фигуры, симметрия которой определяется симметрией кристалла.
Образование и исчезновение вакансий свидетельствует о существовании мест их вытекания и стекания. Такими местами оказываются поверхности кристалла, границы зерен, дислокации, поры и другие размерные дефекты.
Как известно, распределение энергии между атомами твердого тела не является равномерным, в результате чего некоторые атомы могут получить большую тепловую энергию и, преодолев потенциальный барьер соседних атомов, удалиться из узла решетки. "Оседлый" в междоузлии атом основного вещества называют дислоцированным атомом (рис.3.8 б, г). Такой дефект может возникнуть также путем диффузии атома поверхностного слоя внутрь решетки. Энергия образования межузельного атома составляет от 2,5 до 3,5 эВ.

| 
|
| а | б |
| 
|
| в | г |
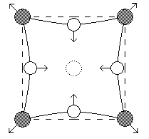
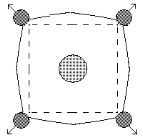
| Рис. 3.8 5.1. Точечные дефекты: а – вакансия; б – межузельный атом; характер смещения атомов в окрестности вакансии (в) и межузельного атома (г) |
Если атом, который находится внутри кристалла, перескочит в межузельное состояние, то одновременно возникают и вакансия, и межузельный атом. Такая пара – вакансия и межузельный атом – называется дефектом Френкеля. Дефекты по Френкелю легко возникают в кристаллах, содержащих значительные межатомные пустоты. Примером таких кристаллов могут служить вещества со структурой алмаза или каменной соли.
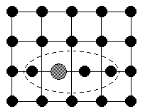
Образование межузельного атома вызывает смещение окружающих его атомов из положений равновесия, причем в некоторых случаях межузельный атом может вытеснить атом из соседнего узла решетки, образовывая вместе с ним так называемую гантель с центром в узле. Такую конфигурацию атомов называют расщепленным междоузлием (рис. 3.9, а). В ГЦК кристаллах ось гантели ориентирована вдоль направления [100], а в ОЦК – [110].
Кроме того, дополнительный межузельный атом может вызывать одномерное сгущение атомов в определенном кристаллографическом направлении, например [110], на длине в несколько межатомных расстояний. Такое сгущение называют краудионом (от англ. crowd - тесниться, толпиться) (рис.3.9, б).

| 
|
| а | б |
| Рис. 3.9 5.2. Расщепленное междоузлие (а) и краудион (б) |
Точечный дефект в первом приближении можно рассматривать как центр сжатия (вакансия) или расширения (атом в междоузлии). Заметное смещение вокруг вакансии наблюдается только в первых двух слоях соседних атомов и его величина составляет доли процента межатомного расстояния (рис.3.8, в). В ГЦК решетках вокруг вакансии ближайшие соседи смещены на –0,84% межатомного расстояния в сторону вакансии. Второй слой смещен по направлению от вакансии на +0,25%, третий на –0,03%. Область, в которой создаются заметные смещения атомов, называется ядром дефекта.
Смещения атомов предопределяют возникновение деформации и упругих полей вокруг дефектов. Для точечных дефектов поля имеют сферическую симметрию, а локальные деформации и напряжения спадают пропорционально 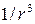 , где
, где 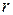 – расстояние от центра дефекта.
– расстояние от центра дефекта.
В ионных кристаллах сохраняется электростатическая нейтральность, если вакансии, которые отвечают ионам разного знака, образуются в таких пропорциях, при которых не нарушается химическая стехиометрия. Пары вакансий с противоположными знаками образуют дефект Шоттки. Точечные дефекты по Шоттки в основном встречаются в кристаллах с плотной упаковкой, где образование межузельных атомов затруднено или энергетически невыгодно.
Одним из наиболее важных и распространенных дефектов структуры реальных кристаллов являются примеси. В зависимости от природы примесей они находятся в кристалле в виде включений или в растворенном состоянии. Процесс растворения заключается в том, что примесные атомы вводятся в промежутки между атомами кристалла или замещают часть этих атомов, располагаясь в узлах решетки. В первом случае твердый раствор называют раствором внедрения (рис.3.9, а), во втором – раствором замещения (рис.3.9, б).
Введение примесных атомов в полупроводники приводит к возникновению в них донорных и акцепторных центров. Если примеси вводятся целенаправленно, то такой процесс называют легированием, а сами примеси – легирующими. Свойства легирующих примесей будут рассмотрены в одном из разделов. Там же будут рассмотрены также такие виды точечных дефектов, как центры окраски и люминесценции.
Кроме легирующих, в полупроводниках имеются также случайные, или как их называют, фоновые примеси, которые появляются в кристаллах в процессе их выращивания и термообработки. Фоновые примеси по большей части ухудшают свойства материалов, поэтому актуальными являются задачи усовершенствования технологии получения кристаллов с низким и контролируемым уровнем фоновых примесей.
 а
а
|  б
б
|
| Рис. 3.9. Твердые растворы: а – внедрения; б – замещения |
Точечные дефекты сильно влияют на многие процессы в кристаллах: на оптические, электрические, магнитные, механические свойства.
Например, тщательно очищенное железо является химически инертным и не окисляется даже в условиях тропической влажности. Титан, хром и другие металлы, которые считаются хрупкими, оказываются очень пластичными после тщательной очистки. Примеси обусловливают и остаточное сопротивление, которое не исчезает при абсолютном нуле.
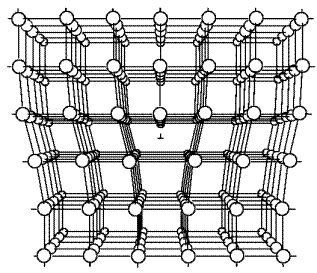
Линейные дефекты. Наиболее важным видом линейных дефектов являются дислокации. Краевую дислокацию можно представить как край «лишней» атомной плоскости в кристалле (экстраплоскости) (рис. 3.10 а). Сам край называется осью дислокации. Наиболее существенным является то обстоятельство, что решетка вблизи края экстраплоскости сильно искажена, – сжата выше края и растянута ниже. Область деформации решетки в непосредственной близости от края экстраплоскости (порядка нескольких параметров решетки) называется ядром дислокации. На больших расстояниях искажения малы и их можно описывать в рамках теории упругости.
Если экстраплоскость находится в верхней части кристалла, то дислокация называется положительной, если в нижней, то отрицательной. Различие между положительными и отрицательными дислокациями является чисто условным.
Простой и наглядный способ введения дислокаций в кристалл – сдвиг. Вычислим усилия, которые необходимо приложить к одной части кристалла, чтобы сдвинуть ее относительно другой, воспользовавшись моделью Я.Френкеля.
| 
|
| а | б |
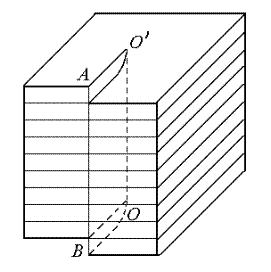
| Рис. 3.10. Простые дислокации: а – краевая; б – винтовая |
Рассмотрим две соседние атомные плоскости А и В в решетке с параметром 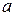 . При смещении плоскости А относительно плоскости В на величину
. При смещении плоскости А относительно плоскости В на величину 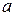 каждый атом этой плоскости попадает в равновесное положение, которое не отличается от предыдущего. В узлах решетки потенциальная энергия атомов является минимальной, а при смещении на величину
каждый атом этой плоскости попадает в равновесное положение, которое не отличается от предыдущего. В узлах решетки потенциальная энергия атомов является минимальной, а при смещении на величину 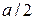 будет максимальной. Соответственно сила межплоскостного взаимодействия двух плоскостей при
будет максимальной. Соответственно сила межплоскостного взаимодействия двух плоскостей при 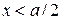 противодействует сдвигу плоскости А от положения равновесия, а при
противодействует сдвигу плоскости А от положения равновесия, а при 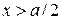 способствует перемещению плоскости А в новое положение равновесия.
способствует перемещению плоскости А в новое положение равновесия.
В первом приближении принимаем, что сила сдвига плоскости А, а следовательно, тангенциальные напряжения 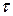 (Па) изменяются по закону
(Па) изменяются по закону
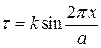 . (3.66)
. (3.66)
Для определения постоянной 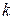 рассмотрим малые смещения, для которых
рассмотрим малые смещения, для которых
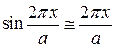 (3.67)
(3.67)
и выполняется закон Гука
 , (3.68)
, (3.68)
где 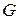 – модуль сдвига;
– модуль сдвига; 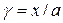 – относительный сдвиг. Следовательно, для малых смещений имеем
– относительный сдвиг. Следовательно, для малых смещений имеем
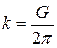 . (3.69)
. (3.69)
Подставляя это выражение в (3.66), получим
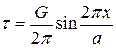 . (3.70)
. (3.70)
Критическое напряжение возникает при 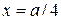 , так что
, так что
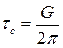 . (3.71)
. (3.71)
При более точном учете межатомных сил значение 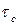 будет несколько меньшим, около
будет несколько меньшим, около 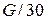 . Модуль сдвига для металлических монокристаллов составляет приблизительно
. Модуль сдвига для металлических монокристаллов составляет приблизительно 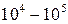 МПа (например, для
МПа (например, для 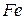
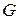 =
= 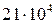 МПа), в то время как в модели одновременного сдвига всех атомов одного слоя относительно другого
МПа), в то время как в модели одновременного сдвига всех атомов одного слоя относительно другого 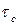 будет составлять
будет составлять 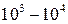 МПа, что на 3–4 порядка превышает экспериментальные значения критического напряжения.
МПа, что на 3–4 порядка превышает экспериментальные значения критического напряжения.
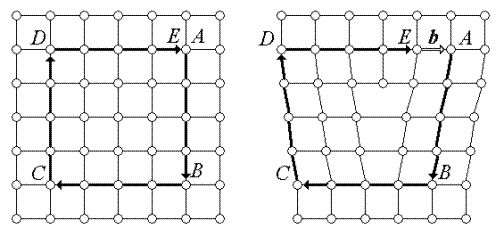
В качестве геометрической характеристики дислокации используется вектор Бюргерса[12] 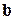 . Проведем вокруг данной дислокации замкнутый контур ABCDE – контур Бюргерса. Этот контур составляется из последовательных трансляций, проведенных от одного узла решетки к ближайшему соседнему, причем число трансляций по сторонам контура одинаково. В идеальном кристалле этот контур окажется замкнутым (рис.3.11, а). Если кристалл содержит дислокацию, он оказывается разомкнутым (рис.3.11, б).
. Проведем вокруг данной дислокации замкнутый контур ABCDE – контур Бюргерса. Этот контур составляется из последовательных трансляций, проведенных от одного узла решетки к ближайшему соседнему, причем число трансляций по сторонам контура одинаково. В идеальном кристалле этот контур окажется замкнутым (рис.3.11, а). Если кристалл содержит дислокацию, он оказывается разомкнутым (рис.3.11, б).
Сдвиг в решетке (вектор Бюргерса  ) перпендикулярен линии краевой дислокации, а сама дислокация перемещается в направлении действия вектора сдвига. Длина вектора Бюргерса кратна единичному вектору решетки. Сдвиг происходит по определенным кристаллографическим плоскостям, например, в кристаллах с ГЦК решеткой по плоскостям {111}. Дислокации могут перемещаться не только в плоскости скольжения, но и перпендикулярно к этой плоскости. Такое перемещение, названное переползанием, обусловливается диффузией. При этом возможен как уход атомов от края экстраплоскости (положительное переползание), так и достройка края (отрицательное переползание). В отличие от скольжения переползание происходит путем переноса массы. Переползание вызывает деформацию кристалла.
) перпендикулярен линии краевой дислокации, а сама дислокация перемещается в направлении действия вектора сдвига. Длина вектора Бюргерса кратна единичному вектору решетки. Сдвиг происходит по определенным кристаллографическим плоскостям, например, в кристаллах с ГЦК решеткой по плоскостям {111}. Дислокации могут перемещаться не только в плоскости скольжения, но и перпендикулярно к этой плоскости. Такое перемещение, названное переползанием, обусловливается диффузией. При этом возможен как уход атомов от края экстраплоскости (положительное переползание), так и достройка края (отрицательное переползание). В отличие от скольжения переползание происходит путем переноса массы. Переползание вызывает деформацию кристалла.
| |
| а | б |
| Рис.3.11. К определению вектора Бюргерса в случае краевой дислокации. Сплошная жирная линия – контур Бюргерса |
Рассмотрим еще один вид дислокации – винтовую. Можно предложить следующую модель образования винтовой дислокации (рис.3.10, б). Сделаем в кристалле разрез по плоскости 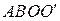 и сдвинем правую (переднюю) часть кристалла на один период решетки вниз. Верхняя атомная плоскость оказывается выгнутой. Таким способом же деформируется и вторая, лежащая под ней плоскость, и все следующие. Причем правая часть каждой плоскости в передней грани смещается на один период и сливается с левой частью следующей за ней плоскости, так что возникает кристалл, который состоит из одной единственной плоскости, закрученной в виде геликоида (винтовых ступенек).
и сдвинем правую (переднюю) часть кристалла на один период решетки вниз. Верхняя атомная плоскость оказывается выгнутой. Таким способом же деформируется и вторая, лежащая под ней плоскость, и все следующие. Причем правая часть каждой плоскости в передней грани смещается на один период и сливается с левой частью следующей за ней плоскости, так что возникает кристалл, который состоит из одной единственной плоскости, закрученной в виде геликоида (винтовых ступенек).
В узкой области вокруг линии 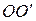 , атомы правой части смещены относительно атомов левой части кристалла. Это смещение вызывает деформацию решетки, которая называется винтовой дислокацией. А сама линия
, атомы правой части смещены относительно атомов левой части кристалла. Это смещение вызывает деформацию решетки, которая называется винтовой дислокацией. А сама линия 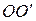 называется осью дислокации. Для описания этого смещения также используют вектор Бюргерса, который для чисто винтовой дислокации параллелен ее оси.
называется осью дислокации. Для описания этого смещения также используют вектор Бюргерса, который для чисто винтовой дислокации параллелен ее оси.
Винтовая дислокация может быть правой или левой. Она параллельна вектору сдвига и не определяет однозначно плоскость сдвига. При скольжении винтовая дислокация перемещается перпендикулярно вектору сдвига и может скользить в любой кристаллографической плоскости, которая содержит дислокацию и вектор сдвига. В отличие от краевой винтовая дислокация может переходить из одной атомной плоскости в другую без переноса массы – поперечным скольжением.
Линия дислокации должна замыкаться внутри кристалла или заканчиваться на его поверхности. Поэтому в общем случае линия дислокации является кривой, отдельные участки которой имеют краевую или винтовую ориентацию, но большая ее часть перпендикулярна и не параллельна вектору сдвига. В этом случае мы имеем дело с так называемой смешанной дислокацией.
Плотность дислокаций, в отличие от точечных дефектов, не подчиняется термодинамическим закономерностям. Дислокации в кристаллах возникают уже в процессе зарождения и роста последних, они могут непрерывно генерироваться при пластической деформации и т.д. Дислокации влияют на различные физические свойства кристаллов, особенно на механические. Низкая прочность кристаллов на сдвиг обусловлена наличием в них дислокаций и их генерацией в процессе сдвига.
Поверхностные дефекты. К поверхностным дефектам относятся границы зерен, блоков, двойников, дефекты упаковки, внешние границы кристалла.
Границей зерна называют поверхность, по обе стороны от которой кристаллические решетки различаются пространственной ориентацией. Взаимную ориентацию решеток соседних зерен характеризуют, указывая общее для обоих зерен кристаллографическое направление 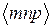 и угол поворота
и угол поворота 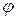 вокруг него, который приводит к полной параллельной ориентации решеток соседних зерен. Если ось вращения лежит в плоскости границы зерен, то такую границу называют наклонной, а если ось вращения перпендикулярная плоскости границы, то имеем дело с границей вращения.
вокруг него, который приводит к полной параллельной ориентации решеток соседних зерен. Если ось вращения лежит в плоскости границы зерен, то такую границу называют наклонной, а если ось вращения перпендикулярная плоскости границы, то имеем дело с границей вращения.
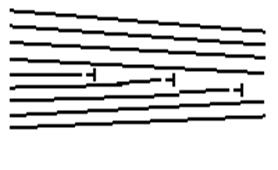
Границы с разориентацией меньше одного градуса называют границами блоков (субзерен), с большей – межзеренными границами. Зерна растут из разных центров кристаллизации, блоки принадлежат одному зерну. К малоугловым границам относят границы с разориентацией менее 100, такие границы образованы системой дислокаций. На рис. 3.12, а представлена схема малоугловой границы для примитивной кубической решетки, которая является стенкой дислокации одного знака. В общем случае малоугловые границы содержат дислокации разного типа и знака.
| 
|
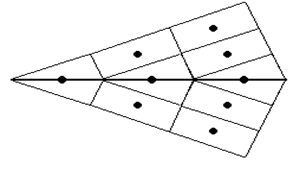
| а | б |
| Рис. 3.12. Граница зерен с малым углом разориентации (а); граница двойника (б) |
Малоугловые границы возникают при росте кристалла из расплава, при пластической деформации, при нагревании после холодной деформации. Границы блоков и зерен являются носителями избыточной свободной энергии, которая обуславливает повышенную скорость протекания химической реакции, диффузии и т.д. Кроме этого на границах происходит рассеяние свободных носителей заряда, что вносит вклад в электрическое сопротивление кристалла.
В кристаллах, которые содержат границы двойников, для которых расположение атомов одной части кристалла является зеркальным отображением другой (рис. 3.12, 6). Такие границы могут возникать в процессе роста кристаллов и при пластической деформации, когда последняя протекает путем двойникования. Развитие двойникования происходит только по определенным кристаллографическим плоскостям, например, в ГЦК решетке по плоскостям (112).
Дефект упаковки – это плоский, двумерный дефект кристаллического строения, который представляет собой нарушение порядка расположения атомных плоскостей. Плоскость дефекта упаковки разделяет кристалл на две части, сдвинутые одна относительно другой на некоторый вектор, не кратный трансляционному вектору решетки и постоянный для всей плоскости дефекта.
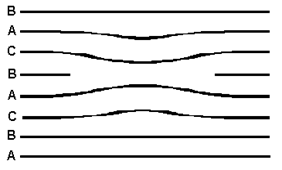
В ГЦК решетках дефект упаковки может возникать либо при введении дополнительного участка плотно упакованной плоскости (111) в решетку (тогда образуется дефект упаковки внедрения (рис.3.13, б), либо при изъятии подобного участка (возникает дефект упаковки вычитания (рис.3.13, а).
| 
|
| а | б |
| Рис.3.13. Дефекты упаковки: вычитания (а), внедрения (б) |
Объемные дефекты. К объемным дефектам относят микровключения других фаз, поры и трещины. Последние два типа дефектов – крайне нежелательны для материала, поскольку искажают практически все его физические свойства, причем наиболее значительно ухудшают прочность и пластичность изделий.
Микровключения других фаз широко используют для улучшения прочности материала. Наилучшие результаты получаются, если кристаллические решетки обеих фаз хорошо согласуются вдоль некоторых плоскостей. Примерами могут служить сплавы алюминия с медью и алюминия с литием. Такие сплавы используются в авиа и ракетостроении как легкий и прочный материал. Но в твердотельной электронике кристаллы, которые содержат такие дефекты, не используются.
Контрольные задания и задачи
1. Чем определяется максимально возможная частота нормальных колебаний решетки?
2. Объясните разницу между акустическими и оптическими колебаниями решетки.
3. Что такое фонон? Чем определяется его энергия.
4. Физическая суть температуры Дебая.
5. Какая причина теплового расширения твердых тел.
6. Чем определяется основная часть теплоемкости металлов в зоне нормальных температур?
7. Почему теплопроводность металлов выше, чем диэлектриков.
8. Объясните механизмы диффузии в кристаллах.
9. Рассчитайте минимальную длину волны Дебая в титане, если его характеристическая температура 278 К, а скорость распространения звука 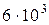 м/с.
м/с.
10. Какая максимальная энергия фононов в кристалле свинца, если его характеристическая температура 94 К?
11. Перечислите типы точечных дефектов и приведите примеры их влияния на свойстве кристаллов.
12. Вычислить равновесную концентрацию вакансий при температуре 300 и 900 К, если энергия образования вакансии равна 1 эВ.
13. Объясните, что такое дислокация. Какие дислокации могут быть в кристаллах?
14. Что такое вектор Бюргерса?
15. Что понимается под переползанием дислокаций?
16. Как влияют дислокации на механические и электрические свойства кристаллов?
17. Дайте определение зерна в кристалле; определение блока.
18. Что такое двойники в кристалле? Как они возникают?
19. Что такое дефект упаковки?
Литература к главе 3
1. Фридрихов, С.Ф. Физические основы электронной техники [Текст]: учеб. / С.Ф. Фридрихов, С.М. Мовнин. – М.: Высш. школа, 1982. – 608 с.
2. Келли, А. Кристаллография и дефекты в кристалах [Текст]: пер. с англ. / А. Келли, Г. Гровс. – М.: Мир, 1974. – 496 с.
3. Уэрт Ч. Физика твердого тела [Текст]: пер. с англ. / Ч. Уэрт, Р. Томсон. – М.: Мир, 1966. – 568 с.
4. Епифанов, Г.И. Физика твердого тела [Текст]: учеб. пособие / Г.И.Епифанов. – М.: Высш. школа, 1977. – 288 с.
5. Гуртов, В.А. Физика твердого тела для инженеров [Текст]: учеб. пособие / В.А. Гуртов, Р.Н. Осауленко. – М.: Техносфера, 2007. – 520 с.
[1] Роберт Гук (англ. Robert Hooke; 1635 –1703) – английский естествоиспытатель, учёный-энциклопедист. Гука можно назвать одним из отцов физики, в особенности экспериментальной, но и во многих других науках ему принадлежат одни из первых основополагающих работ и множество открытий.
[2] Петер Йозеф Вильгельм Дебай (1884 –1966) – голландский физик, лауреат Нобелевской премии по химии за 1936 год. Работы по теории теплоёмкости твёрдого тела при низких температурах (модель Дебая), теплопроводности диэлектрических кристаллов, дипольной теории диэлектриков и др.
.
[3] Шатьендранат Бозе (англ. Satyendra Nath Bose, 1894–1974) – индийский физик, специализировавшийся в математической физике. Один из создателей квантовой механики, статистики (статистика Бозе – Эйнштейна), теории конденсата Бозе – Эйнштейна. В его честь назвали бозон.
[4] Эйнштейн Альберт (1879–1955) – выдающийся физик-теоретик. Творец специальной и общей теорий относительности, значительный вклад внес в развитие квантовой теории света и твердого тела, предсказал явление индуцированного излучения. Создал квантовую статистику частиц с целым спином (статистика Бозе-Эйнштейна). Нобелевская премия за 1921 г.
[5] Пьер Луи Дюлонг (фр. Pierre Louis Dulong; 1785 –1838) – французский химик и физик. Член Парижской академии наук и её секретарь. Основные научные исследования посвящены общей и неорганической химии. Главным научным достижением Дюлонга стал установленный совместно с Пти закон теплоёмкости твёрдых тел.
[6] Пти (Petit) Алексис Терез (1791–1820) – французский физик.
[7] Больцман Людвиг (1844-1906) – австрийский физик-теоретик. Основные работы в области кинетической теории газов, термодинамика и теории излучения. Получил закон распределения молекул идеального газа по импульсам и координатам (статистика Больцмана).
[8] Яков Ильич Френкель (1894 –1952) – советский учёный, физик-теоретик. Круг его интересов был необычайно широк: электронная теория твёрдых тел, физика конденсированного состояния и физика атомного ядра, общие вопросы квантовой механики и электродинамики, астрофизика, гео- и биофизика. Основополагающие работы по квантовой теории твёрдого тела и теории самопроизвольной намагниченности ферромагнетиков, ввёл понятие экситона, представление о дефектах кристаллической решётки («дефекты по Френкелю»), развил молекулярную теорию текучести твёрдых тел, теорию диффузии и вязкости, разработал статистическую теорию тяжёлых ядер, развил электрокапиллярную теорию тяжёлых ядер (капельная модель ядра Бора - Френкеля) и предсказал явление их спонтанного деления.
[9] Вальтер Герман Шоттки (нем. Walter Hermann Schottky; 1886 –1976) – немецкий физик Исследования относятся к физике твердого тела, статистике, электронике, физике полупроводников, термодинамике. В 1915 изобрел электронную лампу с экранной сеткой. Открыл явление возрастания электронного тока насыщения под действием внешнего ускоряющего электрического поля (эффект Шоттки) и разработал его теорию. Предложил супергетеродинный принцип усиления. Рассмотрел пустые узлы кристаллической решетки, нескомпенсированные атомом в междоузлии (дефекты по Шоттки), исследовал потенциальный барьер, образующийся в приконтактном слое «полупроводник – металл» (барьер Шоттки), и построил теорию полупроводниковых диодов с таким барьером (диоды Шоттки).
[10] Адольф Фик (немец. Fick, 1829 –1901) – выдающийся немецкий физиолог.
[11] Джеймс Стирлинг (англ. James Stirling, 1692–1770) – шотландский математик.
[12] Иоханнес (Ян) Мартинус Бюргерс (нидерл. Johannes Martinus Burgers, 1895 –1981) – нидерландский физик, известный открытием уравнения Бюргерса в гидродинамике, вектора Бюргерса в теории дислокаций и материала Бюргерса в теории вязкоупругости. Работал в США.
Дата добавления: 2020-07-18; просмотров: 548;











