Трансляционная симметрия кристаллов

Пространственная решетка Браве отражает трансляционную симметрию кристалла.

Под симметрией тел обычно понимают их свойство совмещаться с самими собой при определенных преобразованиях, которые называются операциями симметрии. Эти преобразования не должны сопровождаться растяжениями, сжатиями, сдвигами и другими деформациями, при которых изменяются расстояния между различными точками тела.

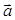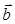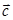Примером преобразования, совмещающего кристаллическую решетку с самой собой, является операция смещения решетки на вектор трансляции , или . Такое смещение решетки, собственно, и называется трансляцией. Нетрудно сообразить, что решетка будет переходить в себя и при трансляции на любой вектор 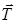, равный линейной комбинации векторов 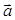, 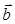и :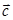

.

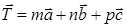(4.3)

Симметрию кристаллической решетки, связанную с трансляциями на вектор трансляции 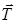, называют трансляционной симметрией.

Так как m, n и p в выражении (4.3) – это произвольные целые числа, существует не один, а целое множество различных векторов трансляции 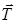. Это множество векторов трансляции называют группой трансляций, а трансляционную симметрию кристалла иногда называют симметрией по отношению к группе трансляций.

Трансляционная симметрия кристаллов отражает периодичность в расположении атомов, ионов или молекул, из которых они состоят. При этом справедливо и обратное утверждение: если система атомов обладает трансляционной симметрией, атомы в системе должны располагаться в пространстве в определенном порядке – регулярно. Поэтому если система атомов обладает трансляционной симметрией, говорят, что такая система обладает дальним порядком в расположении атомов.

Таким образом, кристаллы обладают дальним порядком в расположении атомов.