Результаты практической работы
| Длина линии на местности, м | Численный масштаб | Изображение линии в масштабе |
| 25,65 | 1:500 | |
| 65,1 | 1:1000 | |
| 108,4 | 1:2000 | |
| 171,5 | 1:5000 | |
| 327,0 | 1:10000 |
Условные знаки
Объекты местности изображают на планах и картах условными знаками. Но одни объекты имеют значительные размеры (например, озеро, лес и т. д.), другие объекты малы (колодец, мост и т. д.). Объекты, размеры которых значительны, отображают в масштабе данной карты с сохранением подобия контуров, для малых объектов такое отображение невозможно. Кроме того, и большие и малые объекты необходимо сопроводить определенными характеристиками (для древостоя указать его среднюю высоту, для моста – грузоподъемность и т. д.). В связи с этим все условные знаки делят на три группы: масштабные (контурные), внемасштабные и пояснительные.
Масштабные (рис. 1.8) служат для изображения объектов в масштабе карты или плана. Контур такого объекта наносится точечным пунктиром или тонкой сплошной линией и заполняется значками, отличающими его от других объектов.
Внемасштабные условные знаки (рис. 1.9) применяют для изображения объектов, не выражающихся в данном масштабе. По ним невозможно судить о размерах объекта, но определенная точка знака соответствует положению объекта на местности. Такие знаки используют и для изображения объектов линейного характера (дороги, линии связи и т.д.). Они позволяют передать точное местоположение объектов по их оси.
Промежуточное положение между масштабными и внемасштабными занимают линейные условные знаки, являющиеся по длине масштабными, а по ширине внемасштабными.
| Изображение | Название | Изображение | Название | |
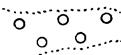
| Лес | 
| Завод | |

| Луг | 
| Труба | |

| Болото непроходимое | 
| Отдельное дерево | |
| Рис. 1.8. Масштабные условные знаки | Рис. 1.9. Внемасштабные условные знаки |
Пояснительные условные знаки (рис. 1.10), представленные значком, числом, надписью или их совокупностью, служат для дополнительной характеристики объектов.
| Изображение | Характеристики |
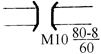
| Моста: М – металлический; 10 – высота, м; 80 – длина, м; 8 – ширина, м; 60 – грузоподъемность, т |
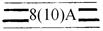
| Шоссе: 8 – ширина покрытия, м; 10 – ширина всей дороги, м; А – материал покрытия (асфальт) |

| Реки: ® 0,5 – направление и скорость течения, м/с |
Рис. 1.10. Пояснительные условные знаки
Условные знаки применительно к различным масштабам приводятся в специальных каталогах, издаваемых Главным управлением геодезии и картографии (ГУГК), и являются обязательными для всех учреждений.
Точное воспроизведение условных знаков – одно из основных требований при вычерчивании плана.
Практическая часть
По двум каталогам условных знаков (для крупного и мелкого масштабов) сопоставить изображения нижеследующих объектов в масштабах 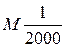 и
и 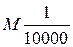 .
.
1. Точки плановых съемочных сетей.
2. Постройки огнестойкие жилые.
3. Линии электропередачи.
4. Воздушные проводные линии связи.
5. Шоссе.
6. Откосы спланированные неукрепленные.
7. Обрывы.
8. Леса.
9. Отдельно стоящие деревья.
10. Сплошные заросли кустарников.
11. Луговая травянистая растительность.
12. Пашни, огороды.
Утвержденные требования к воспроизведению условных знаков приводятся в конце каталогов, в разделе «Пояснения к условным знакам».
Измерение отрезков
Отрезки, длину которых необходимо определить, могут быть прямыми, ломаными и криволинейными.
Измерение прямолинейных отрезков между точками производят с графической погрешностью 0,1 мм, расхождение между повторными измерениями данного отрезка не должно превосходить 0,3 мм.
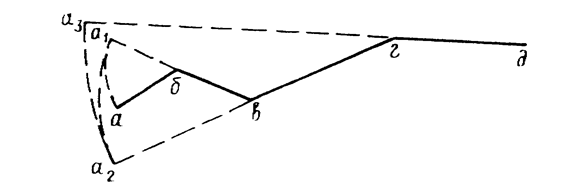
Рис. 1.11. Способ наращивания
Измерение ломаных отрезков производят по частям или путем их последовательного спрямления (способ наращивания). При этом способе (рис. 1.11) устанавливают ножки измерителя в точках а и б, совмещают край линейки с направлением б–в, вращают измеритель вокруг ножки в точке б и устанавливают вторую ножку измерителя у края линейки в точке а1,т.е. на продолжении отрезка бв. После этого перемещают ножку циркуля из точки б в точку в и получают сумму отрезков аб и бв. Действуя аналогично, получают в растворе циркуля а3д общую длину ломаной линии абвгд.
Для контроля измерения проводят в обратном направлении, от точки д к точке а.
Для измерения криволинейных отрезков применяются специальные приборы – курвиметр, циркуль-измеритель с постоянным раствором, а также существует способ наращивания.
Курвиметр состоит из колесика, связанного со стрелкой, которая указывает на циферблате длину линии в сантиметрах. Удерживая курвиметр перпендикулярно к плоскости карты, ведут его колесико по измеряемому отрезку.
Перед применением курвиметра необходимо определить цену его деления. Для этого выбирают отрезок известной длины и устанавливают, какое число делений курвиметра п будет соответствовать этому отрезку. Тогда цена деления курвиметра
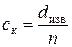 .
.
Перед началом измерения отсчет на циферблате курвиметра выводят на 0.
Применение циркуля-измерителя с постоянным раствором сводится к измерению малых хорд. Берут раствор циркуля порядка двух-пяти миллиметров и определяют по отрезку с известной длиной dизв длину отрезка, взятого в раствор циркуля:
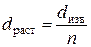 ,
,
где п – число перестановок циркуля. После определения dраст измеряют длину криволинейного отрезка. Для измерений следует пользоваться циркулем с регулирующим винтом, dраст следует брать меньше при большей извилистости измеряемой линии.
Применение способа наращивания при измерении криволинейных отрезков такое же, как и при измерении ломаных отрезков (измеряют малые хорды, на которые делится криволинейный отрезок).
Практика измерений криволинейных отрезков показывает, что наиболее точным является применение циркуля-измерителя с постоянным раствором.
Практическая часть
Сопоставьте точность измерения прямолинейного отрезка тремя способами: по масштабной линейке, циркулем-измерителем с постоянным раствором, с помощью курвиметра.
Перед измерениями, пользуясь графиком линейного масштаба учебной карты, определите цену деления курвиметра ски длину отрезка, взятого в раствор циркуля, dраст.
Измерьте на карте ломаную линию (длину контура: участка, относящегося к населенному пункту) двумя способами: по частям с помощью масштабной линейки и способом наращивания.
Измерьте с помощью курвиметра два криволинейных отрезка: участок реки между сторонами километровой сетки (длина 12 – 14 см) и участок проселочной дороги.
Измерение площадей
Границы участков, площади которых необходимо определить на плане или карте, могут иметь прямолинейное или произвольное очертание.
При прямолинейных очертаниях определение площади возможно двумя способами: графическим (по расчетным формулам конкретных геометрических фигур) и аналитическим (по координатам вершин углов многоугольника).
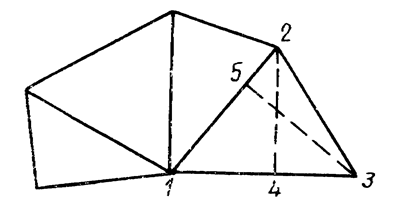
Рис. 1.12. Графический способ определения площади
В первом случае участок разбивают преимущественно на треугольники, реже на прямоугольники и трапеции (рис. 1.12). Измеряют линейные элементы (стороны, высоты) и по формулам геометрии вычисляют площади каждой фигуры. Для контроля площади вычисляют дважды, меняя измеряемые элементы. Например, в треугольнике 1–2–3 в одном случае измеряют основание 1–2 и высоту 3–5, в другом – основание 1–3 и высоту 2–4. Расхождение между двумя значениями площадей не должно превосходить 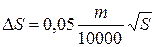 [га], где m – знаменатель численного масштаба. Точность определения площадей примерно
[га], где m – знаменатель численного масштаба. Точность определения площадей примерно 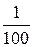 измеряемой величины.
измеряемой величины.
Вычисление площади аналитическим способом, по координатам вершин углов многоугольника, обеспечивает более высокую точность (до 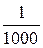 измеряемой величины).
измеряемой величины).
Расчетная формула для определения площади многоугольника (в простейшем случае треугольника – рис. 1.13):
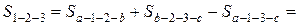
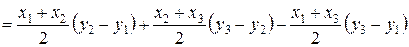 .
.
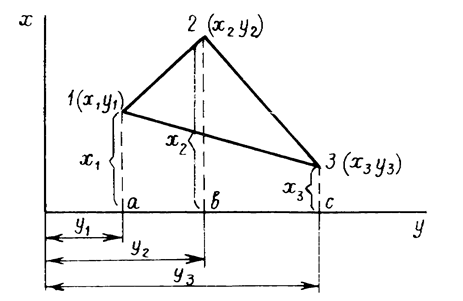
Рис. 1.13. Аналитический способ определения площади
Произведя соответствующие алгебраические действия и преобразования, получим расчетные формулы:
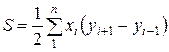 ;
;
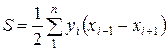 ,
,
где i = 1, 2, 3 ... – номера вершин полигона; 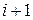 – номер последующей вершины;
– номер последующей вершины; 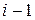 – номер предыдущей вершины.
– номер предыдущей вершины.
При произвольных очертаниях границ участков определение площади возможно также двумя способами: графическим (палетки) и механическим (планиметры).
Для определения площадей небольших участков с криволинейными контурами применяют палетки – квадратные (рис. 1.14) и параллельные (рис. 1.15).

| Рис. 1.14. Квадратная палетка | Рис. 1.15. Параллельная палетка |
Палетки изготавливают на прозрачном материале, расстояние между линиями 1–2 мм. Квадратная палетка применяется для малых участков, имеющих площадь на плане до 2 см2. Подсчитывают число полных клеток, доли неполных клеток учитывают на глаз. Точность измерения примерно 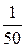 .
.
Параллельную палетку применяют для участков, площадь которых на плане до 10 см2. Палетку на измеряемый контур накладывают так, чтобы точки 1 и 2 расположились между параллельными линиями. Тогда отрезки 3–4, 5–6 и так далее можно считать полусуммой оснований соответствующих трапеций. Найдя суммарную длину этих отрезков и умножив ее на высоту трапеции (т.е. на величину расстояния между параллельными линиями), получим площадь контура.
При механическом способе применяют планиметры различных конструкций, чаще всего – полярный планиметр.
1.6.1. Устройство и поверки планиметра
Полярный планиметр (рис. 1.16) состоит из трех частей: полюсного 1 и обводного 2 рычагов и каретки счетного механизма. Полюсный рычаг с одной стороны имеет груз с иглой 3, которая является полюсом планиметра; перед началом измерений иглу вдавливают в бумагу. С другой стороны полюсный рычаг заканчивается шарниром 6, с помощью которого он соединяется с кареткой счетного механизма. На конце обводного рычага имеется обводный шпиль 7, которым обводят контур участка, удерживая рычаг за ручку 8. Для того чтобы шпиль не царапал карту, существует штифт 9, длину которого можно регулировать с помощью гайки. В более поздней конструкции планиметра шпиль заменен увеличительным стеклом с точкой в центре. На обводном рычаге расположена каретка со счетным механизмом (рис. 1.17). Он состоит из счетного колеса 12, счетчика целых оборотов счетного колеса 13 и верньера 14. При измерении площади участка ободок счетного колеса 15 и ролик 16 должны находиться в пределах листа карты.
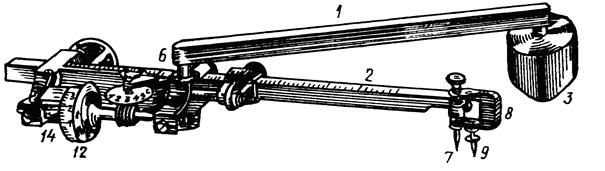
Рис. 1.16. Полярный планиметр
Счетное колесо разделено на 100 делений, каждые 10 делений оцифрованы. Десятые доли делений счетного колеса определяются по верньеру. Делением планиметра называется одна тысячная часть окружности счетного колеса.
Отсчет по планиметру всегда состоит из четырех цифр. Первая цифра – ближайшая к указателю меньшая цифра счетчика оборотов 13, вторая и третья цифры – сотни и десятки делений на счетном колесе, предшествующих указателю верньера 14 (начальному штриху шкалы верньера, т. е. 0); четвертая цифра – номер штриха верньера, совпадающего с каким-либо штрихом счетного колеса (единицы делений). На рис. 1. 17 отсчет по счетному механизму составляет 3578.
Прежде чем приступать к измерению площади, необходимо убедиться в исправности планиметра. Он должен удовлетворять двум условиям.
1. Счетное колесо должно вращаться свободно и без колебаний. Если ось колеса слишком зажата в удерживающих ее центрах или колесо касается примыкающего к нему верньера, то вращение его будет задерживаться и могут возникнуть ошибки при измерениях.
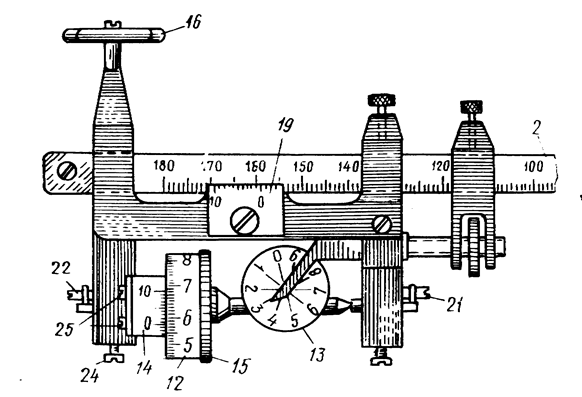
Рис. 1.17. Счетный механизм полярного планиметра
Прежде чем приступать к измерению площади, необходимо убедиться в исправности планиметра. Он должен удовлетворять двум условиям.
1. Счетное колесо должно вращаться свободно и без колебаний. Если ось колеса слишком зажата в удерживающих ее центрах или колесо касается примыкающего к нему верньера, то вращение его будет задерживаться и могут возникнуть ошибки при измерениях.
Поверка выполняется путем вращения счетного колеса рукой. Оно должно вращаться по инерции 3–5 с. Между краем счетного колеса и верньером должен быть зазор не более толщины листа бумаги. Вращение оси счетного колеса регулируется винтами 21 и 22 (см. рис. 1.17). Следует учесть, что при слишком слабом закреплении оси счетного колеса возможно его колебание. Положение верньера относительно края счетного колеса регулируется винтом 25.
2. Плоскость ободка счетного механизма должна быть перпендикулярна оси счетного колеса. Данная поверка выполняется путем обвода контура некоторого участка на бумаге при двух положениях полюса относительно обводного рычага – справа и слева.
Если результаты разнятся между собой не более, чем на 1/250 среднего значения разностей отсчетов, то считается, что планиметр удовлетворяет установленным требованиям. При больших разностях следует производить измерение площадей при двух положениях полюса относительно обводного рычага и счетного механизма. Среднее значение из двух измерений свободно от погрешностей, вызванных нарушением данного условия.
Для измерения площадей с повышенной точностью применяется планиметр ПП-2К. Он имеет две каретки счетного механизма, расположенные с обеих сторон обводного рычага, и, кроме того, обводный шпиль у этого планиметра заменен обводной точкой, выгравированной на нижней поверхности стекла.
Отметим, что в настоящее время имеются и электронные планиметры с индикацией результата измерений на экране дисплея.
1.6.2. Измерение площадей планиметром
Планиметр, используемый для измерения площадей, должен удовлетворять рассмотренным выше требованиям. Необходимо также знать его цену деления и постоянное значение величины q. Если эти величины неизвестны, то их можно определить.
Цена деления планиметра – это площадь, соответствующая изменению отсчета на одно деление. Геометрически ее можно представить как площадь прямоугольника, одна из сторон которого равна длине обводного рычага, а другая – делению планиметра. Цену деления можно выразить в квадратных миллиметрах, если надо измерить площадь участка на бумаге, или, например, в гектарах, когда требуется знать значение измеряемой по карте площади на местности. Для определения цены деления планиметра берется участок, площадь которого заранее известна, затем производится измерение указанной площади планиметром. Обычно для этого пользуются квадратом координатной сетки карты со стороной 10 см. Например, площадь квадрата координатной сетки карты масштаба 1:10 000 равна 100 га.
Обводный шпиль сначала устанавливают в центре квадрата, а полюс закрепляют в такой точке, чтобы угол между обводным и полюсным рычагом был равен примерно 90° и чтобы при обводе квадрата ни одна из опорных точек планиметра не выходила за пределы листа карты. Обводный шпиль подводят к одному из углов квадрата и снимают отсчет u1. Далее шпилем обводят стороны квадрата по ходу часовой стрелки. Возвратившись в исходную точку, снимают второй отсчет u2.
Сместив несколько обводное колесо, вторично производят обвод квадрата против часовой стрелки. При движении по ходу часовой стрелки отсчеты будут возрастать, против часовой стрелки – уменьшаться. Вычитая из большего значения меньшее, находят разности отсчетов, которые не должны отличаться более чем на 5 делений. Проведенные измерения составляют один полуприем. Второй полуприем выполняют в положении полюса с другой стороны обводного рычага и каретки счетного механизма. Расхождение в средних разностях отсчетов при двух полуприемах не должно превышать 5 делений. При наличии сходимости за окончательное значение разности отсчетов принимается среднее из двух результатов.
Цена деления планиметра вычисляется по формуле
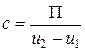 ,
,
где П – площадь измеренного участка; и2 – и1 – средняя разность отсчетов из двух полуприемов.
Цена деления планиметра зависит от положения каретки счетного механизма на обводном рычаге. Перемещая каретку, можно найти такое ее положение, когда значение с будет удобно для измерений, например 1; 0,1; 0,01 и т.п.
Пример.Пусть при обводе квадрата километровой сетки на карте масштаба 1:10000 получена цена деления с = 0,0985 га. Отсчет R по шкале обводного рычага 19 (см. рис. 1.17) составил 159,1 мм. Удобную цену деления планиметра с0 примем равной 0,1 га. Тогда каретку счетного механизма следует переместить на такую величину, чтобы новый отсчет R0 по шкале обводного рычага был равен
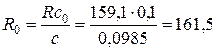 мм.
мм.
Измерение площадей относительно небольших участков (в поперечнике не более 15–17 см) производится с полюсом вне контура. Так же, как и при определении с, шпиль располагают примерно в центре участка, а для полюса выбирают такое место, чтобы рычаги планиметра составляли прямой угол (рис. 1.18, a). Затем производится беглый обвод контура. Угол между рычагами (рис. 18, б,в)должен составлять не менее 30° и не более 150°. Если это условие не выполняется, то подбирается другое, более благоприятное положение полюса. Возможны случаи, когда это не удается, и угол между рычагами выходит за пределы допуска при любом положении полюса. Тогда измерение площадей следует выполнять с полюсом внутри контура (рис. 1.18, г)или по частям.
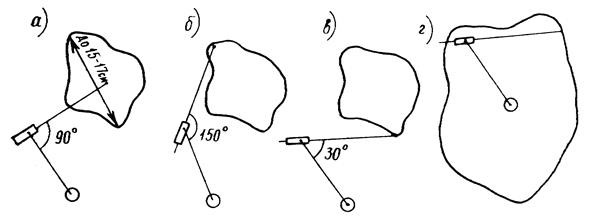
Рис. 1.18. Схемы использования полярного планиметра
Измерение площади участка производится полным приемом, так же как при определении цены деления планиметра. При этом контур участка тщательно обводят шпилем четыре раза: по два раза по ходу и против хода часовой стрелки при двух положениях полюса относительно рычага. Возможно также измерение полуприемом.
Расхождения разностей отсчетов в полуприемах допускаются не более 3–4 делений при величине разностей до 1000 делений и 5–6 делений для участков большего размера.
Площадь участка, измеренная при полюсе вне контура, вычисляется по формуле
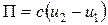 .
.
Значение q планиметра, необходимое при работе с полюсом внутри контура, определяется так же, как и цена деления с,путем обвода контура участка, площадь которого известна. Участок выбирается значительно больших размеров (квадрат 40 ´ 40 см или круг радиусом 30 см). Значение q находится с учетом ранее установленной цены деления с
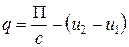 .
.
Площадь с полюсом внутри контура определяется одним приемом и к разности отсчетов добавляется q:
П = с(и2 – u1 + q).
Точность результатов измерений планиметром зависит от многих факторов: точности определения постоянных с и q, конфигурации участка, состояния прибора, деформации бумаги и т. д.
Участки с большим периметром и сложными извилистыми границами (полосы дорог, рек и т.п.) надежнее определять графическим способом. Измерения рекомендуется проводить по карте, тщательно расправленной и закрепленной на гладком столе так, чтобы угол между рычагами по возможности приближался к прямому. При этом следует определять и учитывать деформацию бумаги.
Ошибка определения площади находится приближенно по формуле
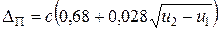 .
.
Упражнение. Определить значение с и q планиметра. Измерить по карте площади двух-трех участков.
Дата добавления: 2016-07-05; просмотров: 2287;











