Рамка с током в магнитном поле
 Поместим прямоугольную рамку 1234 с током I в однородное магнитное поле с индукцией ; нормаль к плоскости рамки расположена под углом α к линиям магнитной индукции. Равнодействующая сил Ампера, с которыми магнитное поле действует на все четыре стороны рамки, равна нулю, но суммарный момент сил нулю равен не будет – рамка будет разворачиваться вокруг оси, перпендикулярной линиям магнитной индукции. Найдём момент сил Ампера – момент пары сил F12 и F34 . Пусть ось, перпендикулярная линиям магнитной индукции – ось z проходит через сторону 12. Единственная сила, которая имеет ненулевой момент относительно этой оси, это сила F34. Её момент
Поместим прямоугольную рамку 1234 с током I в однородное магнитное поле с индукцией ; нормаль к плоскости рамки расположена под углом α к линиям магнитной индукции. Равнодействующая сил Ампера, с которыми магнитное поле действует на все четыре стороны рамки, равна нулю, но суммарный момент сил нулю равен не будет – рамка будет разворачиваться вокруг оси, перпендикулярной линиям магнитной индукции. Найдём момент сил Ампера – момент пары сил F12 и F34 . Пусть ось, перпендикулярная линиям магнитной индукции – ось z проходит через сторону 12. Единственная сила, которая имеет ненулевой момент относительно этой оси, это сила F34. Её момент

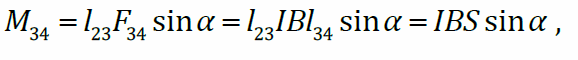 где где S = l23l34 – площадь рамки;
где где S = l23l34 – площадь рамки;
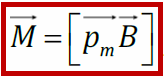 , где
, где 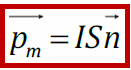 - магнитный момент рамки – характеристика замкнутого проводника (контура) с током (n – нормаль к поверхности рамки); [pm] = А·м2.
- магнитный момент рамки – характеристика замкнутого проводника (контура) с током (n – нормаль к поверхности рамки); [pm] = А·м2.
Вектор магнитного момента показан на 2м рисунке – вид со стороны 23 рамки. Направление магнитного момента выбирается в соответствии с направлением тока в рамке по правилу правого винта.
Магнитное поле стремится развернуть рамку с током так, чтобы её магнитный момент был направлен вдоль линий магнитной индукции.
Методы расчета вектора индукции магнитного поля. Закон полного тока для магнитного поля в вакууме. Применение закона к расчету магнитного поля бесконечно длинного прямолинейного проводника с током, тороида и длинного соленоида.
 (Векторный потенциал)
(Векторный потенциал)
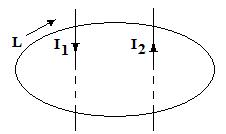 Закон полного тока связывает ток и напряженность магнитного поля.
Закон полного тока связывает ток и напряженность магнитного поля.
На картинке изображены два провода, по которым текут токи I1 и I2. Вокруг токов имеется контур L. Токи проходят через поверхность, ограниченную контуром L. В качестве положительного направления обхода контура выбираем направление по часовой стрелке.
Полный ток – это алгебраическая сумма токов, проходящих через ограниченную замкнутым контуром поверхность.В нашем примере полный ток Σ I есть сумма токов I1 и I2: Σ I = I1 - I2
Знаки токов определяем по правилу буравчика.
Теперь найдём магнитное напряжение вдоль контура L. Разбиваем контур на отрезки, которые можно считать прямолинейными, а магнитное поле в месте расположения отрезков однородным. Магнитное напряжение Um для одного такого отрезка длиной ΔL: Um = HL * ΔL
Магнитное напряжение вдоль всего контура L: UL = Σ HL * ΔL
Полный ток равен магнитному напряжению вдоль контура:
Σ I = Σ HL * ΔL
Это равенство, установленное экспериментально, и связывает токи с напряженностью их магнитного поля.
Магнитное напряжение вдоль замкнутого контура часто называют магнитодвижущей силой. Другое название магнитного напряжения вдоль замкнутого контура – намагничивающая сила.
Определение закона полного тока:Магнитодвижущая сила F вдоль замкнутого контура L равна полному току Σ I, пронизывающему поверхность, ограниченную данным контуром.
Формула закона полного тока:F = Σ I
 1) Расчёт индуктивности длинного соленоида
1) Расчёт индуктивности длинного соленоида
Имеется соленоид длиной l с поперечным сечением S, имеющий плотность намотки n (РИС. 26.5). Длина соленоида много больше его поперечных размеров. Найдем индуктивность соленоида.Пустим по соленоиду ток I. Магнитное поле внутри соленоида однородно.
 , где n - плотность намотки соленоида/
, где n - плотность намотки соленоида/
Магнитный поток сквозь один виток соленоида - 
Потокосцепление -  , Индуктивность соленоида -
, Индуктивность соленоида - 
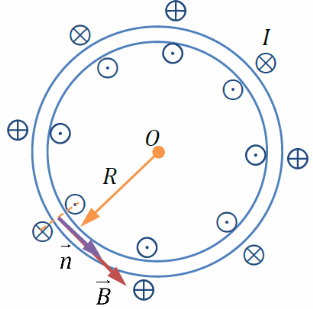 2) Расчёт индуктивности тонкоготороида
2) Расчёт индуктивности тонкоготороида
Тороид – геометрическое тело, образованное вращением плоской фигуры вокруг
оси, лежащей в плоскости этой фигуры.
Найдем индуктивность тонкого тороида радиуса R, сечением S, имеющего N витков. Пустим по тороиду ток I. Модуль магнитной индукции 
Магнитный поток сквозь один виток тороида 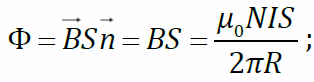
потокосцепление 
Индуктивность тонкого тороида 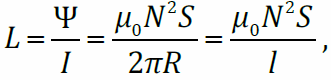 где гдеl = 2πR – длина тороида.
где гдеl = 2πR – длина тороида.
Методы расчет вектора индукции магнитногополя. Закон Био-Савара-Лапласа и его применение к расчету магнитного поля кругового тока (и центре и на оси). Магнитный момент рамки с током.
 (Векторный потенциал)
(Векторный потенциал)
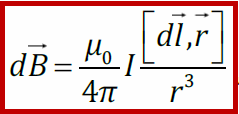
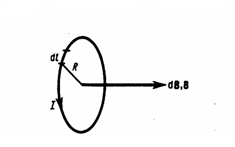
 Закон Био-Савара-Лапласа:индукция магнитного поля точечного тока (бесконечно малого участка тонкого проводника dl с током I).где r – радиус-вектор, соединяющий точечный ток с точкой, где измеряется индукция магнитного поля; μ0 – магнитная постоянная; dlнаправлен по току. Направление dBвыбирается по правилу правого винта. Векторы dlи r лежат в плоскости чертежа, а dBперпендикулярен плоскости чертежа. Модуль элементарной магнитной индукции
Закон Био-Савара-Лапласа:индукция магнитного поля точечного тока (бесконечно малого участка тонкого проводника dl с током I).где r – радиус-вектор, соединяющий точечный ток с точкой, где измеряется индукция магнитного поля; μ0 – магнитная постоянная; dlнаправлен по току. Направление dBвыбирается по правилу правого винта. Векторы dlи r лежат в плоскости чертежа, а dBперпендикулярен плоскости чертежа. Модуль элементарной магнитной индукции 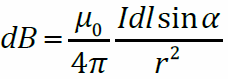
Дата добавления: 2016-07-05; просмотров: 7299;











