Мощности в цепях синусоидального тока

Как было показано выше, мгновенная мощность резистивного (см. рис. 1.6, в) элемента с током i = I_msinωt и напряжением u = RI_msinωt изменяется по закону (рис. 1.23)

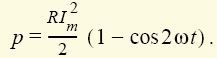
Среднее значение этой мощности

называют активной мощностью.

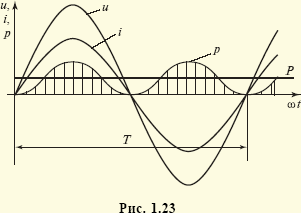
Активная мощность конденсатора и катушки индуктивности равна нулю. Активная мощность пассивного двухполюсника Z (рис. 1.24, а) с сопротивлением Z = Ze^jφ равна Р = UIcosφ, где U и I — действующие значения его напряжения и тока, а φ — угол сдвига между ними.

Наибольшая активная мощность двухполюсника Z (рис. 1.24, а), возможная при данных значениях U и I, называется полной мощностью. Она равна S = UI, а отношение активной мощности Р к полной мощности S, характеризующее его энергетическую эффективность, называется коэффициентом мощности P/S = cosφ. Наряду с активной мощностью для двухполюсника (рис. 1.24, а) вводят понятие реактивной мощности Q = UIsinφ. При этом очевидно, что S² = Р² + Q².

Следует заметить, что в отличие от положительных значений S и Р реактивная мощность может быть как положительной (при активно-индуктивном характере двухполюсника, т.е. при ), так и отрицательной (при активно-емкостном его характере, т.е. при ). Реактивная мощность резистивного элемента равна нулю (Q = 0 при φ = 0). Единицей полной мощности S является вольт-ампер (1 В · А), единицей активной мощности Р — ватт (1 Вт), реактивной мощности — вар (1 вар). Если напряжение и ток двухполюсника заданы комплексами действующих значений , , 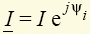то можно ввести комплексную мощность 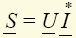, где 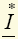— сопряженный комплекс тока 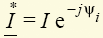. При этом

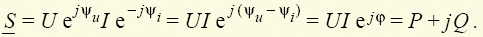
Для комплексных мощностей элементов цепи также справедливо утверждение (теорема Телледжена) о равенстве мощностей, генерируемых источниками (и), и мощностей, потребляемых (п) всеми остальными элементами, т.е. .

Пример 1.6. Для схемы рис. 1.19 имеем .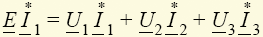

Из приведенного баланса комплексных мощностей следует необходимость выполнения баланса для их активных и реактивных составляющих 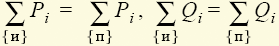(теорема Ланжевена).

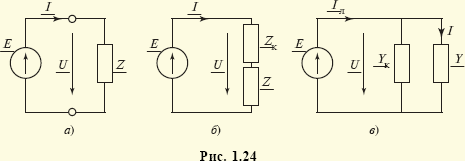
В заключение остановимся на проблеме повышения коэффициента мощности (cosφ → 1), или, что то же, снижения реактивной мощности (|Q| → 0) для генераторов, работающих на комплексную нагрузку Z = R + jX (рис. 1.24, а). Включение последовательно с ней компенсирующего реактивную мощность и не потребляющего активной мощности устройства (рис. 1.24, б) с сопротивлением

Z_к = –jX позволяет при тех же токе I и мощности нагрузки уменьшить мощность генератора (источника) 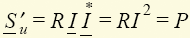, сделав ее чисто активной, и снизить его напряжение Е' = U' = IR. Параллельное нагрузке с проводимостью Y = l/Z = G – jB включение компенсирующего устройства (рис. 1.24, в) с проводимостью Y_к = jB позволяет при тех же мощности S, напряжении U и токе I нагрузки снизить ток в линии и генераторе I_л = GE < I, а также его мощность , которая будет уже чисто активной. Решение проблемы компенсации реактивной мощности повышает эффективность работы соответствующих цепей и позволяет снизить массогабаритные и стоимостные характеристики их элементов. Заметим, что компенсация реактивной мощности по схеме рис. 1.24, б основана на использовании резонанса напряжений, а по схеме рис. 1.24, в — резонанса токов.