Электромагнитные процессы и режимы электрических цепей. Режим синусоидальных токов
Электромагнитные процессы электрических цепей принято делить на установившиеся, когда токи и напряжения всех элементов цепи описываются периодическими функциями времени (как, например, в цепях постоянного и синусоидального токов), и переходные. Последними называются процессы перехода от одного установившегося состояния к другому. Установившиеся процессы принято называть режимами; так, говорят о режиме постоянного тока и режиме синусоидального тока. В последнем случае токи и напряжения всех элементов имеют вид i = Imsin(ωt + ψi), u = Umsin(ωt + ψu), где ω = 2πf— угловая частота; f = 1/T — частота процесса (Т — его период), Im и Um — амплитуды токов и напряжений, а ψi и ωu — их начальные фазы (рис. 1.17).
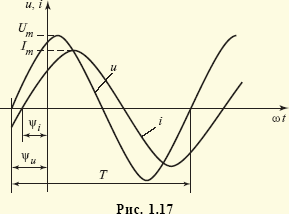
Разность фаз φ = ψu – ψi называется их сдвигом. Из выражений (1.3)—(1.5) следует, что на резисторе фазы напряжения и тока совпадают (φ = 0), на конденсаторе фаза напряжения ψu отстает от фазы тока на угол π/2 (φ = –π/2), а на индуктивной катушке ψu опережает ψi на угол π /2 (φ = π /2). Для оценки интенсивности синусоидальных процессов вводят понятие о действующих значениях токов, напряжений, ЭДС. Для введения этого понятия рассмотрим среднее за период значение мгновенной мощности, характеризующее выделение теплоты в резисторе:
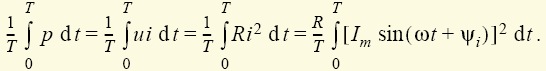
|
Если учесть, что
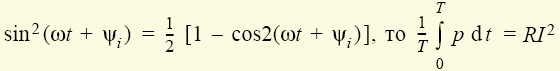 , ,
|
где 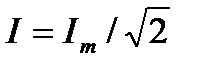 . Величину I называют действующим значением синусоидального тока с амплитудой Im. Численно она равна постоянному току, который вызывал бы в резисторе такие же потери энергии за период времени Т, как и рассматриваемый синусоидальный ток. Действующие значения напряжения U и ЭДС Е также связывают с их амплитудными значениями соотношениями
. Величину I называют действующим значением синусоидального тока с амплитудой Im. Численно она равна постоянному току, который вызывал бы в резисторе такие же потери энергии за период времени Т, как и рассматриваемый синусоидальный ток. Действующие значения напряжения U и ЭДС Е также связывают с их амплитудными значениями соотношениями 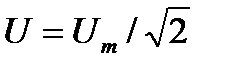 и
и 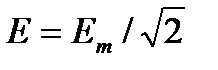 .
.
Режим синусоидальных токов играет особую роль в электроэнергетике, поскольку генерация, передача, распределение энергии происходят в основном именно в этом режиме при частоте f = 50 1/с, или 50 Гц (в США — 60 Гц), называемой промышленной частотой. Поэтому методам описания и расчета такого режима обычно уделяют повышенное внимание.
Основным методом расчета электрических цепей синусоидальных токов (расчета синусоидальных режимов) является комплексный или символический метод, предложенный американским инженером Ч. Штейнмецом. Суть его заключается в том, что каждой синусоидальной функции времени (тока, напряжения, ЭДС) сопоставляется комплексное число, а всем действиям с этими функциями — весьма простые действия с комплексными числами. Так, синусоидальным функциям тока i = Imsin(ωt + ψi) и напряжения u = Imsin(ωt + ψu), графики которых изображены на (рис. 1.17), можно сопоставить комплексные амплитуды 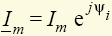 ,
, 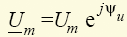 или коплексные действующие значения
или коплексные действующие значения 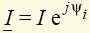 ,
, 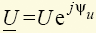 , которые можно изобразить на комплексной плоскости соответствующими векторами (рис. 1.18). Здесь вертикальная ось — ось мнимых чисел, горизонтальная — вещественных чисел. Помимо такой показательной формы записи комплексов I, U, последние можно представить и в алгебраической форме I = ReI + j ImI, U = ReU + j ImU.
, которые можно изобразить на комплексной плоскости соответствующими векторами (рис. 1.18). Здесь вертикальная ось — ось мнимых чисел, горизонтальная — вещественных чисел. Помимо такой показательной формы записи комплексов I, U, последние можно представить и в алгебраической форме I = ReI + j ImI, U = ReU + j ImU.
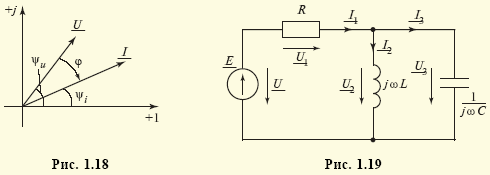
Компонентные уравнения (1.3)—(1.5) в комплексном методе приобретают чисто алгебраический вид U = RI, I = jωCU, U = jωLI, где j — мнимая единица (иначе, оператор поворота)*. Таким образом, схеме рис. 1.10 в этом методе сопоставляется комплексная схема замещения, изображенная на рис. 1.19. Полная система уравнений такой схемы I1 – I2 – I3 = 0, U1 + U2 – U = 0, U2 = U3, U = E, U1 = RI, U2 = jωLI2, 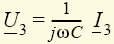 , носит чисто алгебраический характер. Заметим, что последние три уравнения выражают закон Ома для резистивного и двух реактивных (индуктивного и емкостного) элементов.
, носит чисто алгебраический характер. Заметим, что последние три уравнения выражают закон Ома для резистивного и двух реактивных (индуктивного и емкостного) элементов.
Параметры R, ωL = XL и 1/ωС = ХC называют соответственно активным, индуктивным и емкостным сопротивлениями. Решив последние семь уравнений в комплексной области, можно затем от комплексов токов и напряжений всех элементов перейти к соответствующим функциям времени. Комплексным сопротивлением Z (или комплексной проводимостью Y = 1/Z) можно охарактеризовать и любой пассивный двухполюсник (т.е. часть цепи, подсоединенную к остальной цепи двумя узлами). Так, комплексное сопротивление пассивного двухполюсника, подсоединенного к источнику Е, 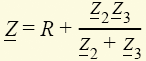 , где Z2 = jωL, Z3 = 1/jωC. Зная его, можно сразу же рассчитать входной ток цепи I1 = U/Z = E/Z.
, где Z2 = jωL, Z3 = 1/jωC. Зная его, можно сразу же рассчитать входной ток цепи I1 = U/Z = E/Z.
Таким образом, комплексный метод расчета позволяет алгебраизовать систему уравнений цепи, а само введение комплексов дает богатые возможности привлечения геометрических построений при суммировании или умножении векторов, соответствующих этим комплексам.
В цепях синусоидального тока особую роль играет понятие резонанса. При резонансе амплитуды тока и напряжения какого-либо участка цепи резко возрастают, а сами ток и напряжение оказываются полностью совпадающими по фазе. Рассмотрим последовательное соединение резистора с сопротивлением R, катушки с индуктивностью L и конденсатора с емкостью С (рис. 1.20, а). Эквивалентное сопротивление этого участка цепи
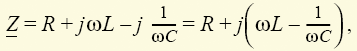
|
а его модуль 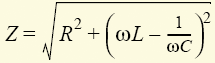 будет иметь минимальное значение Z = R при ωL = 1/ωС. При заданном напряжении участка U ток I будет максимален при минимальном Z = R, фаза тока I = U/Z при Z = R будет совпадать с фазой напряжения. Поэтому рассмотренный случай равенства индуктивного ωL и емкостного 1/ωС сопротивлений как раз и определяет условие резонанса. Очевидно, что достичь условия ωL = 1/ωС можно, изменяя любой из трех параметров ω, L, С. В частности, резонанса можно достичь, меняя угловую частоту до значения
будет иметь минимальное значение Z = R при ωL = 1/ωС. При заданном напряжении участка U ток I будет максимален при минимальном Z = R, фаза тока I = U/Z при Z = R будет совпадать с фазой напряжения. Поэтому рассмотренный случай равенства индуктивного ωL и емкостного 1/ωС сопротивлений как раз и определяет условие резонанса. Очевидно, что достичь условия ωL = 1/ωС можно, изменяя любой из трех параметров ω, L, С. В частности, резонанса можно достичь, меняя угловую частоту до значения 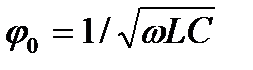 .
.
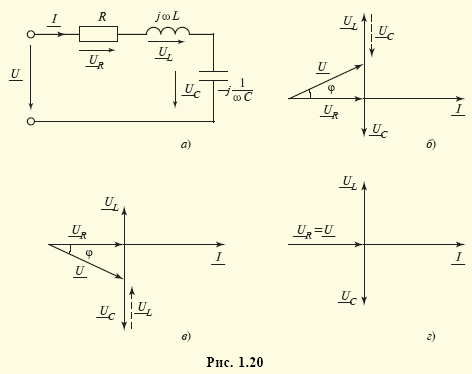
Рассмотрим векторные диаграммы трех случаев соотношений XL = ωL и XС = 1/ωС. В первом случае XL > ХС и цепь носит активно-индуктивный характер, входное напряжение U опережает по фазе ток I цепи (рис. 1.20, б). Во втором случае XL < ХС и цепь носит активно-емкостной характер, напряжение U отстает по фазе от тока I (рис. 1.20, в). В резонансном случае XL = ХС, а напряжение на катушке равно по модулю напряжению на конденсаторе и противоположно по фазе: UL = –UC, они компенсируются, и со стороны входных узлов цепь может рассматриваться как чисто резистивная (рис. 1.20, г).
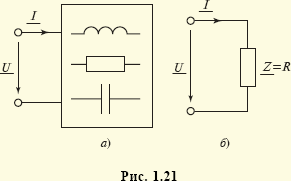
В общем случае мы будем рассматривать некоторый пассивный двухполюсник (рис. 1.21, а), состоящий из резисторов, катушек, конденсаторов и находящийся в условиях резонанса, если его входные ток I и напряжение U совпадают по фазе, т.е. его входное сопротивление Z = U/I носит чисто резистивный характер (Z = R). Такой двухполюсник можно заменить резистивным элементом (рис. 1.21, б).
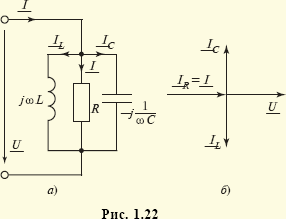
Рассмотрим в качестве еще одного примера резонанс токов, возникающий в цепи, изображенной на рис. 1.22, а, при условии равенства проводимостей катушки 1/ωL, и конденсатора ωС. Токи IL и IC в этих элементах будут равны и противоположно направлены, что графически изображено на векторной диаграмме (рис. 1.22, б). При заданном токе I напряжение U цепи (рис. 1.22, а) будет максимальным по модулю и совпадающим по фазе с током при активной проводимости G = 1/R.
Резонанс на практике играет как положительную, так и отрицательную роль. На основе явления резонанса решается так называемая задача компенсации реактивной мощности (см. следующий параграф), позволяющая достичь наибольшей эффективности передачи электрической энергии в электроустановках и энергосистемах.
Дата добавления: 2016-07-05; просмотров: 2508;











