Классификация подходов к моделированию
Введение в теорию моделирования
Моделирование -процесс замещения исследуемого объекта или процесса его условным образом или другим объектом (моделью) и исследование свойств оригинала на основании анализа свойств модели.
Modeling – создание математической модели
Simulation – компьютерное моделирование
Модель(от латинского modus – копия, образ, очертание) - объект произвольной природы, который отражает важные, с точки зрения решаемой задачи, свойства объекта исследования (оригинала).
Цель моделирования- получение информации о поведении или свойствах реального объекта (процесса).
Условия целесообразности создания моделей:
- Модель устраняет проблемы, связанные с изучением свойств реального объекта.
- Модель обеспечивает адекватное (корректное) отображение исследуемых свойств оригинала.
Формальная классификация моделей(часто строится в форме дихотомий) :
- линейные или нелинейные;
- сосредоточенные или распределённые;
- детерминированные или стохастические;
- статические или динамические;
- абстрактные или материальные;
- дискретные или непрерывные.
- и так далее.
Классификация моделей:
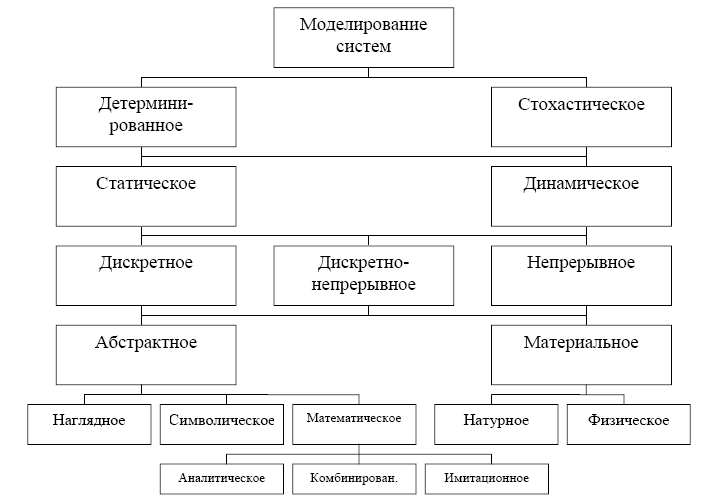
Классификация подходов к моделированию
| Моделирование |
| Математическое |
| Статистическое |
| Физическое |
| Компьютерное |
| Аналитическое |
| Имитационное |
| Численное |
Основные условия выбора подхода обусловлены:
- постановкой задачи;
- составом, характером и объемом исходных данных;
- сложностью объекта моделирования;
- временем на решение исследовательской задачи.
Физическое (натурное) моделирование:
- Измерение характеристик осуществляется на исследуемых системах в реальном времени (проведение экспериментов)
- Данные исследователь получает ведя наблюдение за процессами в реальной системе
Достоинства:
- Высокая адекватность модели реальной системе
- Высокая точность результатов
Недостатки:
- Высокая стоимость создания модели
- Большие временные затраты
- Необходимость доработки отдельных узлов реальной системы для проведения натурных экспериментов
Математическое моделирование:
- Математической моделью называется совокупность математических соотношений, уравнений, неравенств, алгоритмов и т.п., описывающих основные закономерности, присущие изучаемому процессу или объекту (системе).
- Т.е. мат. модель это формализованное описание системы на некотором абстрактном языке, например, в виде математических формул или алгоритма.
Математическая модель цифрового фильтра:

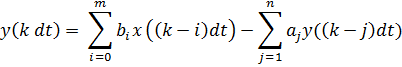
Типы математических моделей:
- Структурные модели представляют объект как систему со своим устройством и механизмом функционирования.
- Функциональные модели отражают только внешне воспринимаемое поведение объекта. В их предельном выражении они называются также моделями «чёрного ящика»
Возможны также комбинированные типы моделей, которые иногда называют моделями «серого ящика».
Иерархия математических моделей:
- Микроуровень – используются распределенные модели (представляются дифференциальными уравнениями в частных производных). В основном такие модели используются для проектирования сложных физических и химических процессов.
- Макроуровень – сосредоточенные модели (линейные и нелинейные дифференциальные уравнения). В таких моделях принято допущение о дискретизации пространства и времени и выделяется одна независимая переменная – время.
- Функционально-логический уровень – здесь абстрагируются от элементов системы и рассматривают систему с помощью аппарата передаточных функций (для аналоговых систем) и аппарата математической логики и конечных автоматов (для дискретных случаев).
- Системный уровень – используется для анализа очень сложных объектов (общество, тел. сети, предприятия и т.д.). Применяют теорию массового обслуживания, сети Петри и т.д.
Основные принципы моделирования:
1. Принцип информационной достаточности.
Информации об исследуемом объекте должно быть достаточно для создания модели.
2. Принцип осуществимости.
Создаваемая модель должна обеспечивать достижение поставленной цели моделирования с определенной вероятностью и за определенный конечный промежуток времени (P(t0)>P0).
3. Принцип множественности модели.
Модель должна отражать исследуемые свойства некоторого семейства объектов.
4. Принцип агрегирования.
Подразумевается возможность декомпозиция модели на элементы и создание моделей отдельных элементов.
5. Принцип параметризации (упрощения модели).
Модели некоторых элементов (связей) могут быть заменены одним или несколькими параметрами.
Аналитическое математическое моделирование:
- Модель представляется совокупностью аналитических выражений, которые отражают явные функциональные зависимости между параметрами реальной системы в процессе ее работы.
- Аналитические модели применяются для относительно простых систем, для исследования характеристик которых не требуется высока точность.
Достоинства
- Простота и низкая стоимость модели.
- Возможность быстро получить численные результаты.
Недостатки
- Большое число допущений и ограничений.
- Не высокая точность результатов .
- Большая сложность аналитического описания. функциональных зависимостей.
Основы имитационного моделирования:
Имитационное моделирование – совокупность методов алгоритмизации, функционирования объектов, описания случайных внешних и внутренних факторов.
Выполняется всегда на ЭВМ в виде вычислительных экспериментов.
Достоинства
- Возможность описания поведения элементов системы на высоком уровне детализации.
- Возможность исследования динамики взаимодействия компонент системы во времени.
- Отсутствие ограничений между параметрами имитационной модели и состоянием внешней среды.
Недостатки
- Меньшая универсальность результатов.
- Необходимость специализированных средств моделирования.
Классификация имитационных моделей:
По способу представления в модели динамики систем:
-На основании событий.
Событие – это мгновенное изменение некоторого элемента системы или системы в целом.
-На основании анализа работы элементов системы.
Работа – это единичное действие по обработке входящих данных.
- На основании анализа процессов.
Процесс – это логически связанный набор работ.
- На основании анализа транзакций.
По способу изменения модельного времени:
- Модели с постоянным шагом.
- Модели, работающие по прерываниям
Алгоритм процесса моделирования:
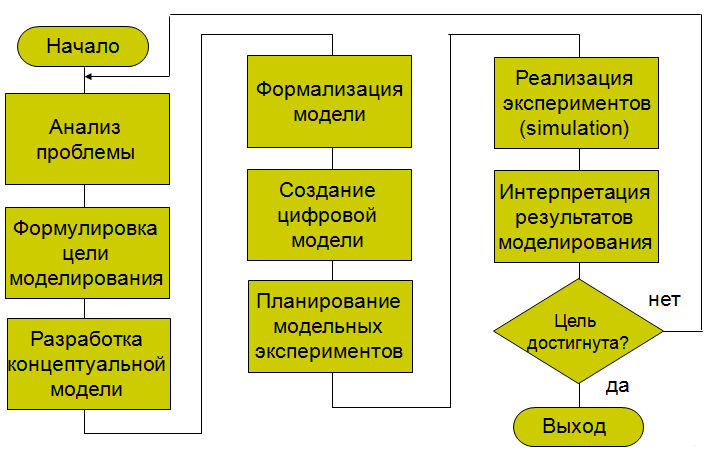
Дата добавления: 2016-07-05; просмотров: 3374;











