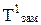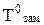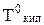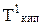Свойства разбавленных растворов неэлектролитов
Свойства раствора всегда отличаются от свойств каждого из компонентов. Это объясняется взаимодействием между компонентами, а также с уменьшением концентрации каждого из веществ при распределении в нем другого вещества. Влияние этих факторов усиливается с ростом концентрации растворов.
Разбавленные растворы приближаются к идеальным. Растворы называют идеальными, если образование таких растворов не сопровождается тепловыми и объемными эффектами (DН = 0, DV = 0), а процесс идет (DG < 0) за счет увеличения энтропии (DS > 0). В таких растворах частицы растворенного вещества находятся на большом расстоянии друг от друга и их взаимное влияние отсутствует, а растворитель не изменяет своих свойств.
Идеальных растворов в природе нет, но многие из них приближаются по своим свойствам к идеальным. Показано, что свойства идеальных жидких растворов, аналогично свойствам газовых смесей, получаются сложением свойств компонентов, то есть являются аддитивными. Другими словами, свойства идеальных жидких растворов зависят только от концентрации растворенного вещества и природы растворителя и практически не зависят от природы растворенных веществ. Такие свойства обычно называют коллигативными (коллективными). Рассмотрим четыре таких свойства.
1. Давление пара растворителя над раствором.Давление насыщенного пара является важным свойством растворов, с которым связан и ряд других свойств. В результате естественного испарения над жидкостью образуется пар. Одновременно с ним протекает экзотермический процесс конденсации. При определенных условиях устанавливается равновесие (DG = 0), которое при данной температуре характеризуется давлением насыщенного пара. При растворении нелетучего компонента в данном растворителе его концентрация уменьшается, и в результате уменьшается число молекул растворителя, переходящих в пар. Это вызывает нарушение равновесия жидкость-пар в сторону процесса конденсации, и давление пара над раствором снижается.
Следовательно, давление насыщенного пара растворителя над раствором (Р1) всегда меньше, чем над чистым растворителем (Р01)
(рис. 6.1).
Рнас.
К/ пар
Рис. 8.1. Диаграмма состояния воды (схема) и влияние на нее растворения нелетучего вещества (прерывистые линии) |
Понижение давления пара будет тем больше, чем больше концентрация (мольная доля χ2) растворенного вещества в растворе:
DР = Р10 · χ2 или 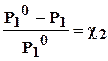 , (6.6)
, (6.6)
где 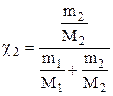 ,
,
m1 , m2 - массы растворителя и растворенного вещества (г), соответственно; М1 и М2 - молярные массы (г/моль.
Таким образом, относительное понижение давления насыщенного пара растворителя над раствором равно мольной доле растворенного вещества.
Это и есть первый закон Рауля.
Пример 11. Имеется 30 %-й раствор глюкозы (С6Н12О6). На сколько понизится давление паров над раствором, если давление чистой воды при 250С равно
23,8 мм рт. ст.?
Решение. Согласно I закону Рауля относительное понижение давления насыщенного пара растворителя над раствором равно мольной доле растворенного вещества в растворе. Найдем мольную долю вещества. Согласно уравнению (6.6)
; 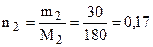 моль (С6Н12О6);
моль (С6Н12О6);
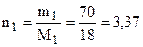 моль (Н2О).
моль (Н2О).
(Напоминаем, что 30 %-й раствор - это 30 г растворенного вещества и 70 г растворителя. Молярная масса глюкозы равна 180 г/моль, а молярная масса воды –
18 г/моль.)
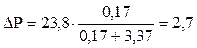 мм рт.ст.
мм рт.ст.
2. Температура кипения (Ткип). Ткип прямо связана с давлением насыщенного пара над жидкостью. Любая жидкость начинает кипеть при температуре, при которой давление ее насыщенного пара достигает величины внешнего давления. На рис. 6.1 показана диаграмма состояния воды.На ней в координатах Р-Т нанесены линии, точки которых показывают равновесные Р и Т между фазами жидкость-лед (аК), жидкость-пар (бК) и пар-лед (КК/). Точка К - тройная точка системы, указывающая Р и Т, при которых в равновесии находятся все три фазы.
Поскольку давление пара растворов, в соответствии с первым законом Рауля, снижается, то, как видно из рис. 6.1, линия Кбсмещается вниз параллельно самой себе; это приводит к смещению точки кипения от б к б/и температуры кипения до 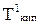 пропорционально концентрации растворенного вещества, т.е. раствор всегда кипит при более высокой температуре, чем чистый растворитель (1-е следствие из закона Рауля).
пропорционально концентрации растворенного вещества, т.е. раствор всегда кипит при более высокой температуре, чем чистый растворитель (1-е следствие из закона Рауля).
Второй закон Рауля для кипения раствора: повышение температуры кипения раствора (DТкип) пропорционально моляльности раствора (Сm):
DТкип = Кэ·Сm ,
где DТкип = (Т1 - Т0); Кэ -эбулиоскопическая постоянная растворителя,
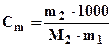 ,
,
где m1 , m2 - массы (г) растворителя и растворенного вещества, соответственно; М2 - молярная масса растворенного вещества, в г/моль.
Для воды КЭ = 0,52 К·кг/моль. Это значит, что растворы, содержащие по 1 моль неэлектролита на 1 кг воды, кипели бы при 100,52°С, если бы растворы такой концентрации были бы идеальными. На самом деле такие концентрированные растворы заметно отклоняются от закона Рауля, поэтому эбулиоскопические постоянные растворителей определяют методом экстраполяции.
3. Температура замерзания (Тзам).Из диаграммы состояния воды (рис. 6.1) видно, что понижение давления насыщенного пара растворителя над раствором смещает и тройную точку в положение К/ . Так как равновесие между жидкостью и твердой фазой почти не зависит от концентрации, то линия Ка смещается параллельно самой себе и точка замерзания а переходит в точку а/. В соответствии с этим температура замерзания Тзам понижается пропорционально (как и Ткип) концентрации: понижение температуры замерзания растворов (DТзам) пропорционально концентрации растворенных веществ.
DТзам = Кк·Сm ,
где DТзам = (Т0 - Т1); Сm – моляльность, Кк -криоскопическая постоянная растворителя, для воды она равна 1,85 К·кГ/моль. Криоскопические постоянные растворителей также находятся методом экстраполяции. Кэ иКкзависят от природы растворителя и не зависят от припроды реагирующих веществ.
Пример 12.При какой температуре будет кипеть и замерзать 30%-й раствор глюкозы ?
Решение.Согласно (6.7) - (6.9):
DТкип = 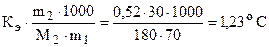 ; tкип = 100 + 1,23 = 101,230 C,
; tкип = 100 + 1,23 = 101,230 C,
DТзам = Кк×Сm 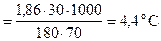 ; tзам = 0 - 4,4 = -4,40 C.
; tзам = 0 - 4,4 = -4,40 C.
Используя уравнения зависимости измения температуры замерзания и кипения от концентрации, можно определить молярную массу вещества. Для этого экспериментально определяют повышение температуры кипения или понижение температуры замерзания раствора.
Таблица 8.1
Криоскопические и эбулиоскопические постоянные
некоторых растворителей
| Растворитель | Кэ | Кк | t кип, 0C | t зам,0C | |
| Формула | Название | ||||
| Н2О | Вода | 0,52 | 1,85 | 0,0 | |
| С6Н6 | Бензол | 2,53 | 5,12 | 80,1 | 5,5 |
| C2H5OH | Этиловый спирт | 1,22 | 1,99 | 78,4 | -11,4 |
4. И наконец, четвертое коллигативное свойство, относится к осмосу - явлению односторонней диффузии через полупроницаемую перегородку, разделяющую раствор и чистый растворитель или два раствора разной концентрации.Такие перегородки (пленки) широко распространены в живой (стенки кишок и мочевого пузыря) и неживой природе (цеолиты); они пропускают молекулы или ионы только определенного размера. Например, тонкие биологические мембраны, отделяющие клетки и разделяющие части клеток, способны пропускать молекулы воды, но не пропускают более крупные молекулы сахара, белков и гидратированные ионы.
Осмотическая ячейка (рис. 8.2) представляет собой два объема, разделенные полупроницаемой перегородкой. В одном из объемов находится растворитель (например, вода), в другом - раствор. Их разделяет полупроницаемая перегородка. В результате односторонней диффузии растворитель переходит в объем раствора, разбавляя его. Это явление создает давление, которое можно определить по высоте столба раствора h. Однако точное значение осмотического давления определяется в эксперименте, в котором уровни объемов 1 и 2 устанавливают одинаковыми с помощью внешнего давления Р, которое в этом случае точно равно осмотическому давлению раствора данной концентрации.
Осмотическое давление возрастает с увеличением концентрации растворенного вещества и температуры, если через перегородку диффундирует только растворитель. Голландский физико-химик Вант-Гофф предположил, что для осмотического давления можно применить уравнение состояния идеального газа, а именно:
Осмотическое давление раствора равно такому давлению, которое создавало бы растворенное вещество в объеме раствора, если бы оно находилось в газообразном состоянии (принцип Вант-Гоффа).
Pосм = CМ·R·T,
где СМ - молярная концентрация раствора (число моль вещества на 1 л раствора) ; R - универсальная газовая постоянная; T - абсолютная температура.
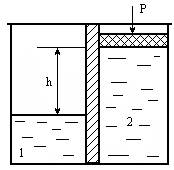
Рис. 6.2. Осмотическая ячейка : 1 - растворитель (Н2О), 2 - раствор,
3 - полупроницаемая перегородка
Осмос играет очень важную роль в биологических процессах, обеспечивая поступление воды в клетки и другие структуры. Растворы с одинаковым осмотическим давлением называются изотоническими. Если осмотическое давление выше внутриклеточного, то оно называется гипертоническим, если ниже внутриклеточного - гипотоническим.
В технике используют обратный осмос, происходящий при приложении к раствору давления, превышающего осмотическое. Тогда через полупроницаемую перегородку "выдавливается" чистый растворитель. Обратный осмос применяется для очистки сточных вод и опреснения морской воды.
Пример 13. Чему равно при температуре -7,50 C осмотическое давление раствора, в 1,5 л которого содержится 276 г глицерина С3Н8О3?
Решение. Согласно закону Вант-Гоффа, Pосм =СМ·R·T.
Найдем, сколько г глицерина содержится в 1 л раствора:
в 1,5 л раствора содержится 276 г глицерина
1 л - x г ,
x = 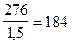 г/л , что составит СМ =
г/л , что составит СМ = 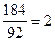 моль/литр = 2·103 моль / м3;
моль/литр = 2·103 моль / м3; 
(92 г /моль - это молярная масса глицерина). Отсюда
Pосм = 2·103 моль/м3·8,31 Па·м3/моль · К·265,5К = 4413·103 Па = 4413 кПа.
Легко видеть, что раствор с концентрацией 1 моль/л создает осмотическое давление 22,4 атм при нормальных условиях.
Изменение коллигативных свойств растворов с изменением концентрации используется на практике: для понижения температуры замерзания жидкостей (например, антифризы - растворы-теплоносители для охлаждения двигателей), а также для расчета некоторых свойств растворов, растворителей и растворенных веществ. Например, по любому из 4-х свойств можно определить молекулярную массу растворенного вещества. Из уравнений (6.6 - 6.10) получаем:
DТкип = Кэ· 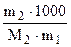 , отсюда
, отсюда 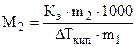 г/моль , (6.11)
г/моль , (6.11)
DТзам = Kк × 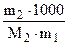 ,
, 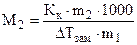 г/моль , (6.12)
г/моль , (6.12)
Pосм = CRT = 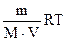 ,
, 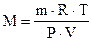 г/моль , (6.13)
г/моль , (6.13)
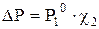 ,
,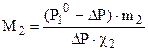 г/моль , (6.14).
г/моль , (6.14).
где m2 и m1 - массы вещества и растворителя (г); M2 - молярная масса растворенного вещества; V - объем раствора (л). Следует, однако, отметить, что найденные по этим формулам величины не являются точными, т.к. формулы верны для идеальных растворов (подобных газовым растворам); на самом же деле растворы отклоняются от идеальных, причем тем больше, чем больше их концентрация.
Пример 14. 0,25 г нелетучего неэлектролита с неизвестной молекулярной массой растворили в 40 г четыреххлористого углерода CCl4. Температура кипения полученного раствора на 0,357О С выше, чем у растворителя (CCl4). Вычислите молекулярную массу растворенного вещества (Кэ ССl4 = 5,3).
Решение. Поскольку речь идет о повышении температуры кипения раствора, воспользуемся уравнением (6.11):
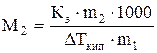 =
= 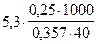 . Отсюда M = 92,78г/моль.
. Отсюда M = 92,78г/моль.
| <== предыдущая лекция | | | следующая лекция ==> |
| Термодинамика растворения и растворимость | | | Классификация подходов к моделированию |
Дата добавления: 2016-07-05; просмотров: 2452;

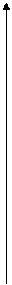
 а/ а 101, 3 кПа б б/
а/ а 101, 3 кПа б б/
 жидкость Р10 ΔР
жидкость Р10 ΔР
 лед К Р1
лед К Р1

 Т
Т