Сведение задачи к самой себе (рекурсия)

.

Рекурсивными называются процедуры и функции, которые вызывают сами себя. Рекурсия позволяет очень просто (без использования циклов) программировать вычисление функций, заданных рекуррентно, например факториала f(n)=n!:

f(0)=1 f(n)=n*f(n-1).

Рекурсивные процедуры являются удобным способом порождения многих комбинаторных объектов. Мы заново решим здесь несколько задач предыдущей главы и вы убедитесь, что запись многих алгоритмов значительно упростится благодаря использованию рекурсии.

Факториал

Еще раз напомним рекурсивный алгоритм вычисления факториала:

program Factorial;

var N:word;

function F(n:word):longint;

begin

if n=0 then F:=1 else F:=n*F(n-1)

end;

begin

write('N=');readln(N);

writeln('N!=',F(N))

end.

Ханойская башня

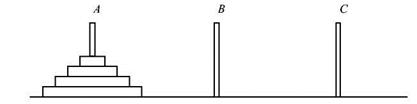
Игра "Ханойская башня" состоит в следующем. Есть три стержня. Hа первый из них надета пирамидка из N колец (большие кольца снизу, меньшие сверху). Требуется переместить кольца на другой стержень. Разрешается перекладывать кольца со стержня на стержень, но класть большее кольцо поверх меньшего нельзя. Составить программу, указывающую требуемые действия.

Hапишем рекурсивную процедуру перемещения M верхних колец с A-го стержня на B-ый в предположении, что остальные кольца больше по размеру и лежат на стержнях без движения:

procedure Move(M,A,B:integer);

var C:integer;

begin

if M=1 then begin writeln ('сделать ход ',A,'->',B) end

else

begin

C:=6-A-B; {C - третий стержень: сумма номеров равна 6}

Move(M-1,A,C);

Move(1,A,B);

Move(M-1,C,B)

end

end;

Сначала переносится пирамидка из M-1 колец на третий стержень C. После этого M-ое кольцо освобождается, и его можно перенести на B. Остается перенести пирамиду из N-1 кольца с C на B. Чем это проще первоначальной задачи? Тем, что количество колец стало на единицу меньше. Теперь основную программу можно записать в несколько строк:

program Hanoi;

var N:integer;

procedure Move(M,A,B:integer);

.............

begin

write('N=');readln(N);

Move(N,1,2)

end.

Таким образом, ОСHОВHАЯ ИДЕЯ любого рекурсивного решения - свести задачу к точно такой же, но более простой (с меньшим значением параметра). Эта более простая задача имеет ту же формулировку, что и исходная, с той лишь разницей, что решаться она должна для более простых исходных данных. При этом какое-то минимальное значение параметра должно давать решение без рекурсивного вызова - иначе программа "зациклится" (последовательность рекурсивных вызовов будет бесконечной). В некоторых задачах удобно наоборот, увеличивать значение параметра при рекурсивном вызове.