Рекурсия и итерация.

Рекурсия- это определение понятия самого через себя.

Например, идентификатор ::= <буква>|<идентификатор><буква> |<идентификатор><цифра>

В случае процедур и функций рекурсия используется в виде вызова функции самой себя в собственном теле. Это делается обычно для последовательного понижения размерности (сложности) задачи, пока решение задачи не станет тривиальным (простым). Запись решения задачи в виде последовательности рекурсивных вызовов функции обычно выглядит более понятно (более просто) по сравнении с обычным (нерекурсивным ) (итерационным) решением.

Например, одно и то же вычисление факториала можно сделать несколькими способами:

Нерекурсивное (итерационное) решение:

fact(n) =1*2*3*4*...*n =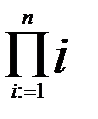

Рекурсивное решение имеет вид:

1, при n=0

Понижение размерности задачи

fact(n) =

fact(n-1)*n при n >0.

4!=(3!)*4

Примеры итерационных вычислений, например, при вычислении значений многоместных (n-арных) операций уже рассматривались выше (когда роль идет о вычислении n – арных операций)

Вычисление с помощью итерации: Рекурсивное определение той же функции:

Предопределенная

константа

Type type

natural=0.. maxint; natural=0.. maxint;

function fact(n: natural): Longint; function fact(n: natural): Longint;

var begin

i: integer; if n = 0 then

f: Longint; fact := 1;

begin else fact := n * fact(n-1); end;

f:= 1; end.

for i:= 1 to n do вычисление значения этого

f:= f * i; выражения будет производиться

fact := f; на рекурсивном возврате (после

end; рекурсивного вызова)

переменная где формируется

результат функции

Процесс рекурсивного вычисления значения в данном случае факториала организуется в соответствии с данным определением. Этот процесс сводится к последовательному вызову функции самой себя каждый раз с новым значением аргумента (цепочке рекурсивных вызовов). При этом каждый раз при каждом таком рекурсивном вызове в стеке откладывается копии всех локальных параметров процедуры или функции:

Fact(3) à 3*Fact(2) à 3*( 2* Fact(1) ) à 3*( 2*( 1* Fact(0)))

Нерекурсивный вызов Fact(0)=1 завершает цепочку рекурсивных вызовов.

В общем случае при вызове любой процедуры или функции происходят следующие действия:

1). В стеке сохраняются значения локальных объектов подпрограммы (фактические параметры и локальные для вызываемой подпрограммы переменные);

2). Запоминается адрес возврата в вызывающую подпрограмму (или программу);

3). Управление передается вызванной подпрограмме.

В некоторый момент выполнения программы в стеке может присутствовать несколько (возможно даже одинаковых) групп локальных объектов, соответствующих цепочке вызванных, но не завершенных подпрограмм. В каждый момент времени доступ возможен только к той группе, которая включена в стек последней и находится в голове стека. Эта группа локальных объектов соответствует текущей вызванной подпрограмме. Таким образом, в случае, если в стеке оказывается одновременно несколько одноименных переменных, то доступна их будет лишь та, которая попала в стек последней. При завершении вызванной подпрограммы ее локальные объекты удаляются из вершины стека, и в голове стека оказываются (и становятся доступными) локальные объекты вызывающей подпрограммы.

Рассмотрим процесс рекурсивного определения более подробно на примере вызова y:=fact(3).

Fact(3) Первичный вызов n 3

Fact ? 6

Fact(2) n 2 fact(2)*3

спуск рекурсивные вызовы Fact ? 2 возврат

Fact(1) n 1 fact(1)*2

Fact ? 1

Fact(0) n 0 fact(0)*1

содержимое стека Fact 1

имя

значения имя при рекурсивных вызовах

вычисляемые значения при рекурсивных возвратах

Такой процесс последовательного вызова функции самой себя естественно с разными значениями аргумента называется рекурсивным спуском. В процессе рекурсивного спуска при каждом рекурсивном вызове в стеке выделяется память под копию каждого локального параметра. Процесс рекурсивного спуска будет продолжаться до тех пор, пока выражение в правой части оператора присваивания для вычисления возвращаемого значения не примет вполне определенный вид (в этом случае функция сама себя не вызывает). В данном случае конец наступит, когда при очередном рекурсивном вызове аргумент будет равен 0, после этого процесс начнет раскручиваться в обратную сторону - будет происходить рекурсивный возврат. Этот процесс сопровождается освобождением памяти(в стеке), занимаемой очередной копией локальных объектов процедур или функций.

Действия в теле рекурсивных процедур и функций могут выполняться либо на рекурсивном спуске (до рекурсивного вызова) , либо на рекурсивном возврате (после рекурсивного вызова). В данном случае действие (вычисление факториала) происходит в процессе рекурсивного возврата и имеет следующий вид:

то, что получено после рекурсивного вызова

fact(n) = fact(n-1) * n.

Количество вызовов функцией самой себя при рекурсивном спуске называется глубиной рекурсии.

Необходимыми условиями для успешного завершения рекурсии процедур или функций являются следующие:

1). необходимо точно определить ситуацию, при которой должен завершиться рекурсивный спуск. В данном случае такая ситуация имеет вид: n =0 - один признак у этой ситуации Но может быть и более сложный случай.

2) необходимо предусмотреть в теле рекурсивной подпрограммы тех действий, которые должны приближать наступление указанной выше ситуации.

Каждую рекурсию можно заменить итерацией, применив цикл. Рекурсивное определение алгоритма обычно более просто и компактно. Можно считать, что при рекурсивном определении говорится, что нужно сделать, но не говорится как. При итерационном наоборот: строго формулируется, что и как нужно сделать.

У рекурсивной процедуры или функции имеются следующие недостатки: на выполнение рекурсии процедуры или функции требуется большое количество машинного времени и памяти.

Времени требуется больше потому, что многократно вызываются процедуры и функции, т.е. тратиться время на то, чтобы выйти и войти в нее. Память тратится больше из-за того что при каждом рекурсивном вызове резервируется память в стеке для каждого локального объекта процедуры или функции. Для контроля переполнения стека используется директива {$S+}. Для сокращения памяти в стеке (при этом увеличатся затраты памяти в сегменте данных) при рекурсивном вызове (при предполагаемом большом числе рекурсивных вызовов), целесообразно использовать статические локальные переменные - на Паскале это типизированные константы (память под них выделяется не в стеке, а сегменте данных).

Не каждый алгоритм может быть успешно реализован с помощью рекурсии. Успешно алгоритм может быть реализован, если удалось определить ситуацию, при наступлении которой завершится процесс рекурсивного спуска.