Моделирование параллельных процессов. Сети Петри.

Виды параллельных процессов

Существует 2 вида параллельных процессов (ПП):

- асинхронные ПП – состояние которых не зависят от состояния других ПП;

- синхронные – состояние которых зависят от состояния других ПП.

В рамках синхронных ПП выделяют:

- подчиненный ПП – создается и управляется другим процессом;

- независимый ПП – процесс не являющийся подчиненным ни для одного процесса.

Обеспечение параллелизма

Для обеспечения параллелизма в вычислительных системах используются 3 основных подхода:

- на основе «взаимного исключения»;

- на основе синхронизации посредством сигналов;

- с использованием специализированных протоколов и сообщений.

Методы описания параллельных процессов

Для описания параллельных вычислительных систем часто используется математический аппарат конечных автоматов.

Автомат – математическая абстракция, описывающая реальную систему, которая определяется набором внутренних состояний.

Q={q₁, q₂, … q_N}

Если N – конечное число, то такой автомат конечный.

Автомат имеет конечное число входов и выходов. Входы и выходы связанны между собой посредством состояний автомата. Работа автомата описывается в дискретном времени.

Моделирование в сетях Петри осуществляется на событийном уровне. Определяется, какие действия происходят в системе, какие состояния предшествуют этим действиям, и какие состояния будет иметь система в результате таки действий.

Основные понятия

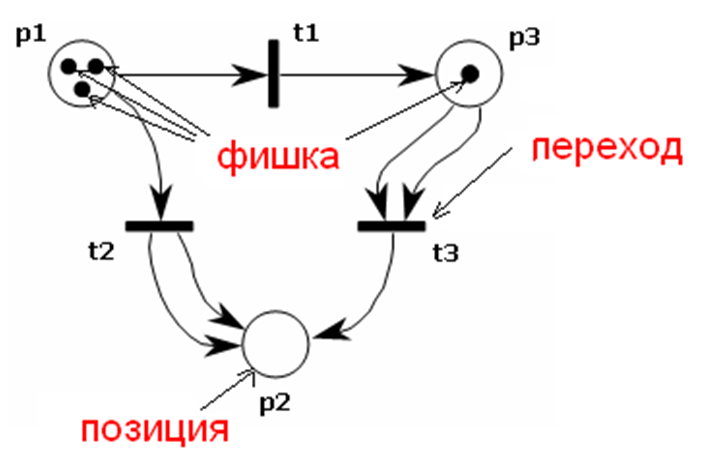
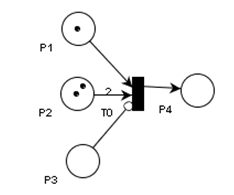
Сеть Петри – это помеченный ориентированный двудольный граф.

Все вершины графа относятся к одному из двух классов - позициям и переходам. Позиции изображаются окружностями, переходы - отрезками прямой. Дуги в сетях Петри - направленные. Причем каждая дуга связывает вершины только разных классов.

Аналитическое описание сетей Петри

Простая сеть Петри представляет собой функцию, зависящую от следующих элементов:

N={S, T, F}

l S – множество позиций S={S1, S2, … SN}

l T – множество переходов T={t1, t2, … tm}

l F – отношение идентичности (описывает, каким образом связанны между собой позиции и переходы)

Основные понятия:

Виды позиций:

- входная позиция некоторого конкретного перехода – позиция, из которой исходят дуги, входящие в данный переход.

- выходная позиция некоторого конкретного перехода - позиция, в которую входят дуги, исходящие из данного перехода.

Фишка (маркер). Фишки изображаются точками, расположенными внутри позиций. Каждой позиции сети ставится в соответствие натуральное число, указывающее количество фишек в данной позиция. Это число называют разметкой позиции, а совокупность таких чисел для всех позиций сети называют разметкой сети.

Правила срабатывания переходов в сети Петри

Срабатывание перехода состоит в изъятии фишек из каждой входной позиции и помещении их в каждую выходную позицию. Причем, количество фишек, изымаемых из конкретной позиции, или помещаемых в конкретную позицию равно количеству дуг, соединяющих срабатывающий переход с данной конкретной позицией.

Определения

- Позиция может и не содержать фишек, т.е. иметь нулевую разметку.

- Разметку сети до срабатывания любого перехода называют начальной или стартовой разметкой.

- Последовательное срабатывание переходов и соответствующее изменение разметки сети называют процессом функционирования (выполнения) сети.

- Завершение процесса функционирования приводит сеть к разметке, называемой конечной

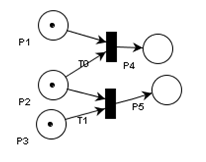
Виды сетей Петри:

- Временные сети Петри – каждый переход описывается своей задержкой во времени. Моделируются динамические характеристики системы.

- Цветные сети – используются несколько видов маркеров. Каждый из видов имеет свой цвет.

- Стохастические сети – предполагают наличие случайных факторов в сети (случайная задержка позиции, направление перехода)

- Сети Петри с ингибиторными дугами.

Преимущества использования сетей Петри в моделировании и анализе:

- большие выразительные способности в представлении параллельных асинхронных систем;

- способность представления локального управления, параллельных, конфликтных, недетерминированных и асинхронных событий;

- графическое и аналитическое представление сети;

- понятность модели и легкость ее изучения;

- возможность иерархического моделирования на их основе;

- возможность описания системы на различных уровнях абстракции;

- возможность представления системной иерархии;

- возможность машинной поддержки в проектировании.

Свойства сетей Петри:

- Ограниченность

- Сохранение

- Активность

- Достижимость и покрываемость

- Эквивалентность и включение

Предметом теоретического исследования сетей Петри является процесс их функционирования, т.е. возможные последовательности срабатывания переходов и свойства получаемых при этом разметок сети.

Ограниченность

Под ограниченностью понимают свойство сети не допускать превышения количества фишек в конкретной или произвольной позиции некоторого фиксированного числа.

Позиция сети Петри ограничена (k-ограничена), если существует такое целое число k, что число объектов в этой позиции никогда не превышает k. Число k называют емкостью позиции. Сеть Петриограничена, если ограничены все ее позиции.

Если известны емкости всех позиций, и наибольшая из них kmax, то сеть называют kmax-ограниченной.

Сеть, все позиции которой 1-ограничены, называют безопасной

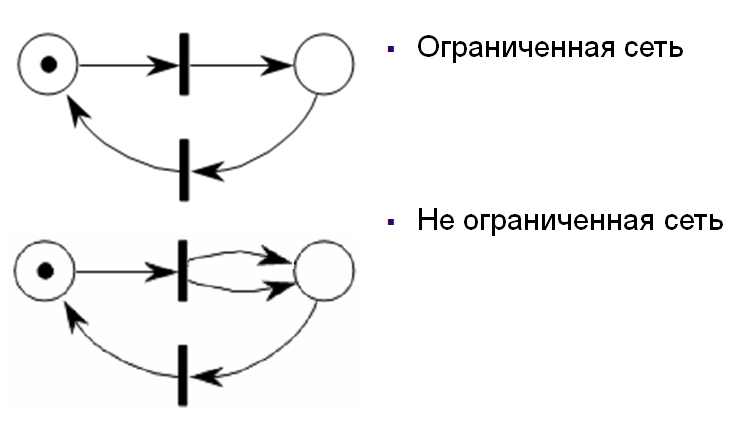
Сохранение

Сеть Петри называют сохраняющей, если число циркулирующих в ней объектов постоянно.

∙

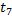
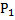
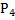
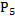
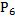
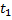
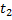
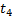
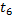
Активность

Переход сети Петри называют тупиковым, если в процессе функционирования сеть может оказаться в состоянии, в котором этот переход заблокирован. Нетупиковый переход называют активным.

- активность уровня 0, если он никогда не может быть активирован (пассивный переход);

- активность уровня 1, если существует состояние (достижимое из начального), в котором он активирован;

- активность уровня 2, если для всякого целого n существует последовательность срабатывания переходов, в которой данный переход присутствует по крайней мере n раз;

- активность уровня 3, если существует бесконечная последовательность срабатывания переходов, в которой данный переход присутствует неограниченно часто;

- активность уровня 4, если для любого достижимого состояния существует последовательность срабатываний, приводящая в такое состояние, в котором этот переход активирован (активный переход).

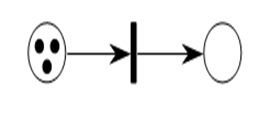
Пример сети всегда приходящей к тупиковой разметке.

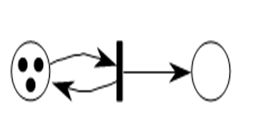
Сеть никогда не "попадает в тупик"

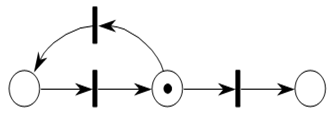
Сеть, которая может остановиться, а может и нет

Достижимость и покрываемость

Состояние Sдостижимо в сети Петри, если существует цепочка срабатываний переходов, ведущая из начального состояния в S. Состояние S'=(P1'...Pn') покрывает состояние S"=(P1"...Pn"), если для каждого i=1, ...,n имеет место Pi' Pi", т.е. имеет место S' S".

Задача достижимости (покрываемое™) состоит в том, чтобы для данной сети и состояния S определить достижимо ли S (достижимо состояние, покрывающее S). Задачи достижимости и покрываемости можно рассматривать применительно к набору не всех, а лишь некоторых позиций, т.е. к подсостояниям сети Петри.

Эквивалентность и включение

Сети Петри эквивалентны, если они имеют одинаковое поведение, определяемое множеством достижимых состояний или множеством реализуемых последовательностей переходов.

Сеть СП1, включается в сеть СП2, если поведение СП1 является подмножеством поведения СП2.