Первые модели надежности ПО

Как известно, на данный момент времени разработано большое количество моделей надежности ПС и их модификаций. Каждая из этих моделей определяет функцию надежности, которую можно вычислить при задании ей соответствующих данных, собранных во время функционирования ПС. Основными данными являются отказы и время. Другие дополнительные параметры связаны с типом ПС, условиями среды и данных.

Первые модели надежности ПО были тесно связаны с теорией надежности аппаратуры и использовали экспоненциальный закон распределения вероятности безотказной работы ПО.

4.2.1 Модель Джелински, Моранда и Шумана [32]. Эта модель надежности ПО, известная также как модель роста надёжности, была разработана Джелински и Морандой [37] и Шуманом [38]. Модель опирается на теорию надежности аппаратуры. Считается, что это наиболее известная модель надежности ПО. Итак, пусть известны [32]:

R(t) – функция надежности, т. е. вероятность того, что ни одна ошибка не проявится на интервале от 0 до t;

F(t) –функция отказов: вероятность того, что ошибка проявится на интервале от 0 до t;

Z(t) – условная вероятность того, что ошибка проявится на интервале от t до t+dt, при условии что до момента t ошибок не было.

Т – время появления ошибки.

Тогда эти величины связаны соотношением:

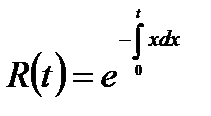, (4.1)

Для экспоненциального закона распределения вероятности безотказной работы:

Rt=exp⁡(-λt) (4.2)

Модель использует результаты наблюдения за поведением программы в течение длительного периода времени. Если нанести на график время между последовательными ошибками, то получим зависимость, показанную на рис. 4.1. Рис. 4.1 иллюстрирует явление роста надежности по мере того как ошибки обнаруживаются и исправляются, время между последовательными ошибками становится больше. Каждая ступенька на рис. 4.1 – это выявленная ошибка, высота последовательных ступенек одинаковая, а ширина растет. Со временем увеличивается интервал между последовательным обнаружением ошибок. Экстраполируя эту кривую, можно предсказать число ошибок и когда они проявятся. Экстраполяция основана на имеющемся распределении вероятностей ошибок. Сведения о найденных ошибках можно использовать для оценки параметров распределения и для предсказания отказов в будущем [32].

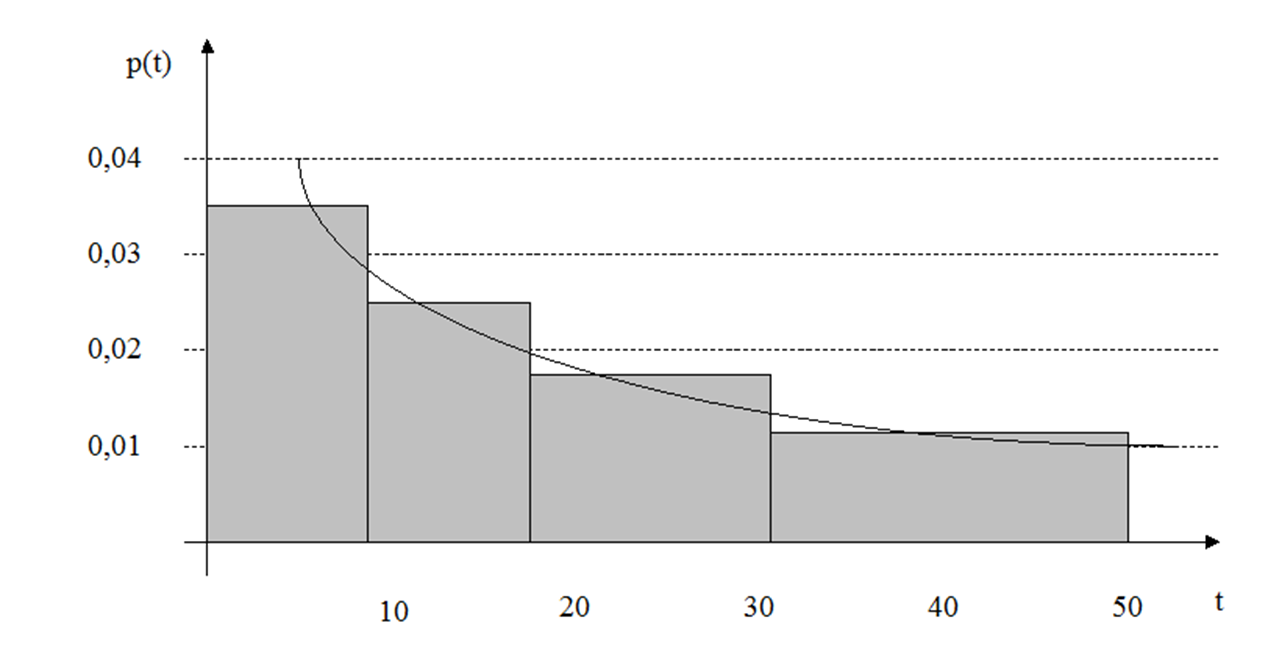
Рисунок 4.1 – Вероятность безотказной работы ПО (на рисунке Р(t) – это R(t))

Модель Джелински, Моранда и Шумана предполагает, что один из способов оценки среднего времени между отказами – наблюдение за поведением программы в течение некоторого периода времени и нанесение на график значений времени между последовательными ошибками. Можно надеяться, что при этом будет обнаружено явление роста надежности; по мере того как ошибки обнаруживаются и исправляются, время между последовательными ошибками становится больше. Экстраполируя эту кривую в будущее, можно предсказать среднее время между отказами в любой момент времени и предсказать полное число ошибок в программе.

Такая экстраполяция, однако, в слишком большой степени основана на догадках и обычно уводит в сторону. Было бы лучше опираться на какое-то априорное представление об имеющемся распределении вероятностей ошибок, затем использовать сведения о найденных ошибках для оценки параметров этого распределения и только потом использовать эту модель для предсказания событий в будущем.

Разработка такой модели начинается с уточнения поведения функции λ(t)– интенсивности отказов ПО.В большинстве моделей аппаратного обеспечения λ(t) сначала уменьшается со временем (этап, когда обнаруживаются и исправляются ошибки проектирования и производства), затем остается постоянной в течение большей части срока службы системы (соответствует случайным отказам) и в конце полезного срока службы системы увеличивается (см. рис. 1.2). В теории надежности аппаратуры в основном рассматривается средний период, где интенсивность отказов постоянна. Однако предположение о постоянстве интенсивности отказов вряд ли применимо в случае программного обеспечения, для которого эта функция должна уменьшаться по мере обнаружения и исправления ошибок. Поэтому, как показано на рис. 4.2, интенсивность отказов со временем уменьшается.

Рисунок 4.2 – Предполагаемая интенсивность отказов ПО

Дополнительная критика модели роста надежности [47]. Всякая модель строится на допущениях и предположениях, причем многие из них- спорны. Одно из первых предположений состоит в том, что все ошибки одинаково серьезны (например, полный отказ в процессе работы системы и синтаксическая ошибка в команде одинаково важны). Такое предположение легко снять, если разбить все ошибки на классы в соответствии с их серьезностью и дать разные оценки для всех классов.

Второе предположение – то, что ошибка исправляется немедленно или программа не используется до тех пор, пока найденная ошибка не будет исправлена. Предполагается, что программа не изменяется (за исключением исправления ошибок). Третье предположение – при всех исправлениях найденные ошибки устраняются, и новых ошибок не вносится. Конечно, основное предположение – это то, что для всех программ функция Z(t) подобна изображенной на рис. 4.1. Тем самым предполагается, что каждая ошибка уменьшает Z(t) на постоянную величину

Достаточно спорно предположение о том, что значение Z(t) постоянно между ошибками. Надежность программного обеспечения является функцией числа ошибок, их серьезности и их взаимного расположения, а также того, как система используется. Сторонники постоянства Z(t) между ошибками считают, что входные данные системы являются скорее повторяющимися, чем случайными.

Гипотезы о поведении Z(t) на рис. 4.1 демонстрируют некоторый рост надежности. Частота отказов в большой системе при измерении в течение нескольких лет может иметь тенденцию к понижению. Анализ частоты обнаружения ошибок при тестировании в 14 различных программных системах показал, что частота эта в пяти проектах достигала пика в начале работы, в пяти – в середине и в четырех – в конце. Таким образом, «рост надежности» скорее желателен, чем обязателен.

Чтобы еще более усложнить этот вопрос, можно утверждать, что каждая программа имеет свое собственное, уникальное распределение Z(t)) и даже что для каждой новой инсталляции программы Z(t)– свое.

Таким образом, в некоторых случаях, модель роста надежности кажется чересчур оптимистичной.

4.2.2 Статистическая модель Миллса. В 1972 г. суперпрограммист фирмы IBM Харлан Миллс предложил [39] следущий способ оценки количества ошибок в программе. Пусть у нас есть программа. Предположим, что в ней N ошибок. Назовем их естественными. Внесем в нее дополнительно s искусственных ошибок. Проведём тестирование программы. Пусть в ходе тестирования было (n+v) ошибок, причем п – число найденных собственных ошибок, a v – число найденных внесенных ошибок. Предположим, что вероятность обнаружения для естественных и искусственных ошибок одинакова. Таким образом, сначала программа «засоряется» некоторым количеством известных ошибок. Эти ошибки вносятся в программу случайным образом, а затем делается предположение, что для ее собственных и внесенных ошибок вероятность обнаружения при последующем тестировании одинакова и зависит только от их количества. Тестируя программу в течение некоторого времени и отсортировывая собственные и внесенные ошибки, можно оценить N – первоначальное число ошибок в программе.

Предположим, что в программу было внесено s ошибок, после чего было решено начать тестирование. Пусть при тестировании обнаружено (n+v) ошибок, причем п – число найденных собственных ошибок, a v – число найденных внесенных ошибок. Тогда оценка для N (первоначального числа ошибок в программе) будет такой:

N=s nv (4.3)

Вторая часть модели связана с выдвижением и проверкой гипотез об N. Примем, что в программе имеется не более k собственных ошибок, и внесем в нее еще s ошибок. Теперь программа тестируется, пока не будут обнаружены все внесенные ошибки, причем в этот момент подсчитывается число обнаруженных собственных ошибок (обозначим его n). Эта формула для N образует статистическую модель ошибок и предсказывает число ошибок

Критика модели Миллса. Процесс внесения ошибок является самым слабым местом модели. Предполагается, что для собственных и внесенных ошибок вероятность обнаружения одинакова, но заранее неизвестна. Из этого следует, что внесенные ошибки должны быть «типичными» образцами ошибок.