Краткие теоретические основы

Решение прямых и обратных задач геофизики методом цифровой фильтрации (на примере задачи гамма-каротажа)

Краткие теоретические основы

При компьютерной обработке результатов гамма-каротажа используют методику дифференциальной интерпретации, в основе которой лежит представление каротажной кривой как суммы гамма-полей, создаваемых тонкими пропластками с равномерным распределением урана внутри каждого такого пропластка. Такое допущение справедливо благодаря свойству аддитивности гамма-поля: процесс радиоактивного распада происходит независимо для всех ядер изучаемой среды.

В общем случае интенсивность гамма-излучения I(z) в точке z по оси скважины может рассматриваться как сумма интенсивностей гамма-излучения от бесконечно большого числа бесконечно тонких пропластков. Каждый такой пропласток характеризуется определенным содержанием урана. Математически это выражается следующей формулой:

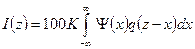, (1)

где: K - пересчетный коэффициент, q(x) - содержание урана в % по оси скважины, Y(x) – так называемая весовая функция или функция «отклика среды», характеризующая интенсивность гамма-поля по оси скважины x над бесконечно тонким пластом, расположенном в точке z.

Обратная задача ГК заключается в нахождении распределения содержаний урана по оси скважины, т.е. в определении q(z) по функции J(z). Решение уравнения (1) относительно q(z) получают в следующем виде:

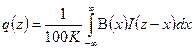, (2)

где B(x) - т.н. обратная функция отклика среды, которая может рассматриваться как оператор (фильтр высоких частот или дифференцирующий фильтр), позволяющий определять вклад каждого бесконечно тонкого пропластка в формирование интегрального гамма-поля по стволу скважины. Этот вклад пропорционален содержанию урана в тонком пропластке, что и отражено в формуле (1).

Прямая Y(x) и обратная B(x) функции отклика среды зависят не только от координаты x, но и других параметров, в частности, плотности руды r и жидкости в скважине r_о, радиуса скважины r, толщины обсадных труб, размера детектора, и др. Y(x) и B(x) - четные функции , т.е. Y(x) = Y(-x), B(x) = B(-x).

Так как гамма-поле быстро затухает по оси x (практически полностью при x > 50 см), то пределы интегрирования в формуле (2) могут быть изменены на конечные. Хотя интеграл (2) не имеет аналитического решения в силу произвольного характера функции I(z), его значение можно найти с помощью численного интегрирования.

С достаточной точностью интеграл (2) вычисляется по формуле

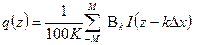, (3)

где: q(z) - содержание урана (в %) по скважине в точке z; I(z - kDx) - интенсивность гамма-излучения в точке z - kDx; Dx = const - интервал между соседними точками вычисления содержаний урана (интервал дискретизации или квантования); k - индекс суммирования, изменяющийся от -M до M с шагом 1; B_k = B(kDx) - значения обратной функции отклика среды, взятые с интервалом дискретизации Dx.

Рекомендуемое оптимальное значение Dx составляет 10 см. При больших интервалах дискретизации каротажной диаграммы увеличивается погрешность выделения границ рудных зон, а при меньших - возрастает погрешность решения обратной задачи ГК.

Если пронумеровать по порядку точки отсчетов интенсивностей гамма-поля I_n = I(z_n) = I(nDx), n = 0, 1, ... N, то формулу (3) можно переписать в следующем виде:

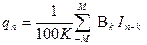. (4)

где q_n - содержание урана в n-й точке.

В результате интерпретации получают распределение массовой доли урана по скважине с интервалом Dx = 10 см. Возможно появление отрицательных значений содержаний q_n. Появление большого количества отрицательных значений q_n (более 5 % от размеров выборки M) свидетельствует о неправильном расчете коэффициентов B_k или о том, что M £ 3.

Среднее содержание урана в границах рудных зон находят вычислением среднеарифметического значения q_n.