Пример канонического метода структурного синтеза автомата.
Выполним структурный синтез частичного автомата А, заданного своими таблицами переходов и выходов (табл. 23 и 24.).
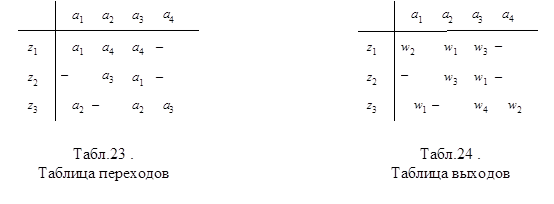
|
Синтез будем выполнять в следующем порядке:
1. Выберем в качестве элементов памяти D-триггер, функция входов которого представлена в таблице стр. 33.
2. Закодируем входные, выходные сигналы и внутренние состояния автомата. Количество входных абстрактных сигналов F = 3, следовательно количество входных структурных сигналов L= ]log2F [ = ]log23[ = 2, т.е. х1, х2.
Количество выходных абстрактных сигналов G = 4, следовательно количество выходных структурных сигналов N =]log2G[ = ]log24[ = 2, т.е. у1, у2. Количество внутренних состояний абстрактного автомата M = 4, следовательно количество двоичных элементов памяти (триггеров) R = ] log2M [ = ]log24[ = 2.
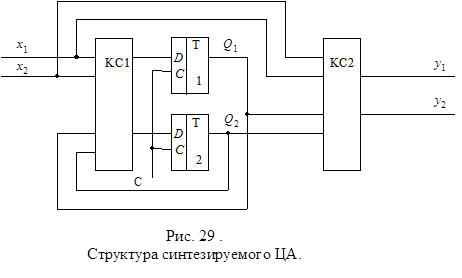
|
Следовательно, структура ЦА с учетом того, что исходный автомат является автоматом Мили, в качестве элементов памяти используется D-триггер, может быть представлена в виде(рис. 29):
Кодирование входных, выходных сигналов и внутренних состояний представлена в таблицах:
| x1 | x2 | y1 | y2 | Q1 | Q2 | |||||||
| z1 | w1 | a1 | ||||||||||
| z2 | w2 | a2 | ||||||||||
| z3 | w3 | a3 | ||||||||||
| w4 | a4 |
Кодирование, в общем случае, осуществляется произвольно. Поэтому, например, каждому из сигналов Zi можно поставить в соответствие любую двухразрядную комбинацию х1, х2. Необходимо только, чтобы разные выходные сигналы Zi кодировались разными комбинациями х1, х2. Аналогично для Wi и ai.
3.Получим кодированные таблицы переходов и выходов структурного автомата. Для этого в таблицах переходов и выходов исходного абстрактного автомата вместо Zi, Wi, ai cтавим соответствующие коды. Получим таблицы:

| a1 | a2 | a3 | a4 | a1 | a2 | a3 | a4 | |||||
| Z1 | – | Z1 | – | ||||||||||
| Z2 | – | – | Z2 | – | – | ||||||||
| Z3 | – | Q1Q2 | Z3 | – | y1y2 |
В кодированной таблице переходов заданы функции 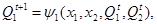
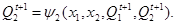
В кодированной таблице выходов заданны функции:

4.При каноническом методе синтез сводится к получению функций:
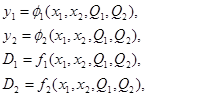
и последующем построении комбинационных схем, реализующих данную систему булевых функций.
Функции у1 и у2 могут быть непосредственно получены из таблицы выходов, например, в виде :
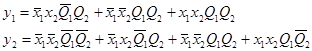
Однако выражения для у1 и у2 можно существенно упростить в результате минимизации, например, с помощью карт Карно:
 10 10
| |||||||||||
| – | – | ||||||||||
| – | – | – | – | ||||||||
| – | – | ||||||||||
| – | – | – | – | – | – | – |  – –
|

В результате минимизации имеем:
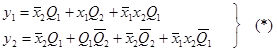
Для получения выражений для D1 и D2 необходимо получить таблицы функций возбуждения. Для чего в общем случае необходимо воспользоваться таблицей переходов и функциями входов элементов памяти. Зная код исходного состояния автомата и код
состояния перехода на основании таблицы входов триггера получаем требуемое значение функции возбуждения, обеспечивающее заданный переход. Однако для D-триггеров, как отмечалось ранее, таблица переходов совпадает с таблицей функции возбуждения. Тогда либо непосредственно из этой таблицы, либо в результате минимизации получаем требуемые значения Di. Обычно используется минимизация с помощью карт Карно:

| |||||||||||
| – | – | ||||||||||
| – | – | – | – | ||||||||
| – | – | ||||||||||
| – | – | – | – | – | – | – | – |
В результате минимизации получаем:
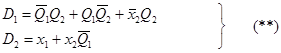
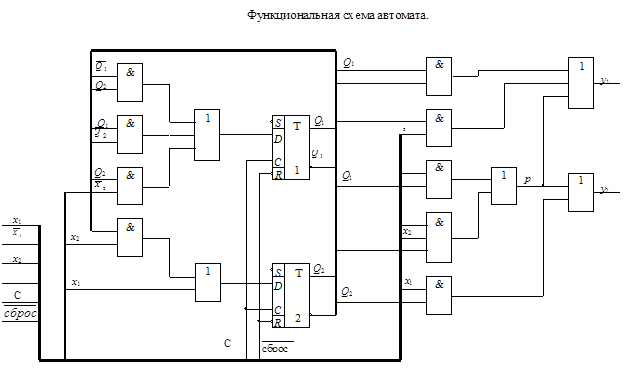
5.На основании полученных в результате синтеза булевых выражений ((*), (**)) ,строим функциональную схему автомата. Для этого уравнения ((*), (**)) представим в виде:
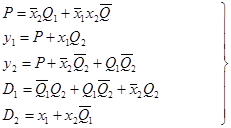
Функциональная схема автомата представлена на странице 41:
Дополнительно на функциональной схеме показан сигнал 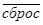 , устанавливающий автомат в начальное состояние (в данном случае 00).
, устанавливающий автомат в начальное состояние (в данном случае 00).
Особенности синтеза автоматов на базе T, RS, JK триггеров.
Необходимо отметить, что синтез на базе указанных типов триггеров осуществляется аналогично выполненному синтезу на базе D-триггеров. В частности, п. 1¸3 (см. предыдущий параграф) абсолютно аналогичны. Кроме того, как следует из п.4 (см. предыдущий параграф) выходные сигналы не зависят от типа триггеров, поэтому выражение для yi будут одинаковыми для любого типа триггеров. Однако функции возбуждения будут различны для разных типов триггеров и получаются на основании таблицы переходов исходного автомата и функции входов выбранного триггера. Без особых пояснений ниже приведены таблицы функций входов, функций возбуждений и карты Карно для минимизации функций возбуждения при использовании для синтеза автомата предыдущего параграфа T-, RS-, JK-триггеров.
T-триггер.
| Q t | Q t+1 | T t |

| – | ||||
| – | – | |||
| – |
| – | – | ||||||||||
| – | – | – | – | ||||||||
| – | – | ||||||||||
| – | – | – | – | – | – | – |

RS-триггер.
| Q t | Q t+1 | R | S |
| X | |||
| X |

| R1 | S1 | R2 | S2 | R1 | S1 | R2 | S2 | R1 | S1 | R2 | S2 | R1 | S1 | R2 | S2 | |
| X | X | X | – | – | ||||||||||||
| – | – | X | – | – | ||||||||||||
| X | – | – | X | X |

| |||||||||||
| X | – | X | – | ||||||||
| – | – | – | – | ||||||||
| X | – | – | X | ||||||||
| – | – | – | – | – | – | – | – |

| X | – | – | |||||||||
| – | – | – | X | – | |||||||
| – | – | X | |||||||||
| – | – | – | – | – | – | – | – |

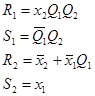
JK-триггер.
| Q t | Q t+1 | J | K |
| X | |||
| X | |||
| X | |||
| X |
| J1 | K1 | J2 | K2 | J1 | K1 | J2 | K2 | J1 | K1 | J2 | K2 | J1 | K1 | J2 | K2 | |
| X | X | X | X | X | X | – | – | |||||||||
| – | – | X | X | X | X | – | – | |||||||||
| X | X | – | – | X | X | X | X |
| X | – | X | X | – | |||||||

| – | X | – | – | X | – | |||||
| – | X | X | X | – | |||||||
| – | – | – | – | – | – | – | – |
| X | X | – | X | – | |||||||
| – | X | X | – | – | – | ||||||
| X | – | – | X | ||||||||
| – | – | – | – | – | – | – | – |

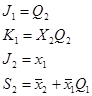
Функциональные схемы автоматов с различными типами триггеров предлагается построить самостоятельно.
Дата добавления: 2020-06-09; просмотров: 717;











