Проверочный расчет зубьев на изгибную выносливость

Определение допускаемых напряжений:

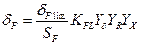
Y_d-коэффициент, учитывающий градиент напряжений;

Y_R-коэффициент, учитывающий шероховатость поверхности;

Y_X-коэффициент, учитывающий размеры зубчатого колеса;

d_Flim-предел выносливости зубчатого колеса;

S_F-коэффициент безопасности.

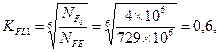
но не менее 1, принято равным 1;

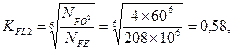
но не менее 1, принимаем равным 1.

S_F=2,2

Yd=1,1, d_R=1, Y_X=0

[d_F1] =[d_F2]=[d]_F

d_Flim=1,8НВ=1,8 х 38=576

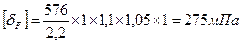
Действующие напряжения изгиба равны:

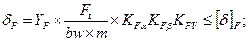
Y_F-коэффициент формы зуба;

Y_F=4,8 – принимается в зависимости от числа зубьев эквивалентного колеса:

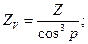
b=0; Z_V=Z

K_FV=1,13 – из таблиц в зависимости от окружной скорости и степени точности

K_Fa=1 для прямозубых зубчатых передач

K_Fb=1,05 в зависимости от j_bd;

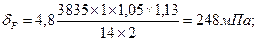
d_F<[d_F], 248<275 мПа,

зубья проходят по изгибной выносливости.

5.3 Подбор чисел зубьев в планетарной передаче.

При проектировании планетарных механизмов наиболее трудоемким этапом в расчете геометрии является подбор чисел зубьев. Широко применяемым методом подбора является метод сомножителей.

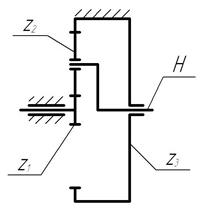
При выборе схемы механизма следует руководствоваться ве­личиной передаточного отношения U₁₂. Заданное передаточное отно­шение обеспечивается подбором числа зубьев z₁, z₂, z₃, z₄.

При подборе чисел зубьев необходимо обеспечить несколько условий одновременно. Это УСЛОВИЕ СООСНОСТИ, УСЛОВИЕ СОСЕДСТВА, УСЛОВИЕ СБОРКИ центрального, корончатого колес и сателлитов. Условие соосности способствует обеспечению равенства межосевых расстояний центрального колеса и сателлитов. Условие соседства обеспечивает размещение сателлитов без задевания одного другим. Условие сборки обеспечивает возможность собираемости N-oгo количества сателлитов после установки первого так, чтобы зубьям сателлитов обеспечивалась возможность расположения во впадинах центрального и корончатого колес одновременно.

Сущность подбора чисел зубьев методом сомножителей состоит в том, что отношение чисел зубьев, входящих в формулу для опре­деления передаточного отношения U₁₂ представляется отношением так называемых сомножителей С₁, С₂, С₃, С₄. Затем записывается ус­ловие соосности для данной схемы планетарного механизма (свое для каждой схемы), в котором неизвестное число зубьев выразится через известные сомножители. Далее, налагая условие сборки (пра­ктически одинаковое для всех схем планетарных механизмов), по­лучают искомое число зубьев. Например, для схемы 2 (см. рис 7) передаточное отношение определяется формулой:

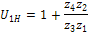
и равно числу 5,20, которое можно представить суммой 1+4,20 или иначе 1+42/10=1+21/5. Последнюю дробь можно представить в виде произведения двух сомножителей числителя и двух сомножителей знаменателя, и тогда формулу для определения передаточного отношения можно переписать в цифровом выражении введя сомножители С1, С2, С3, С4:

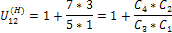
Имеется двухступенчатый планетарный редуктор с общим передаточным числом 48,84

Выбираем передаточное число первой ступени u_ред.1 = 8.

Тогда передаточное число второй ступени редуктора u_ред.2 = 6,11.

1 < U < 10 1 < U < 10

u_ред.1 =8 u_ред.1 =6,11

ПЕРЕДАТОЧНОЕ ОТНОШЕНИЕ

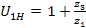
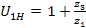
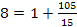
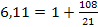
ЧИСЛО ЗУБЬЕВ ИЗ УСЛОВИЯ СООСНОСТИ ПО МЕТОДУ СОМНОЖИТЕЛЕЙ

z₁=γ c₁ z₁=γ c₁

15=5*3 21=3*7

z₃=γ c₃ z₃=γ c₃

105=5*21 108=3*36

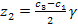
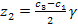
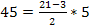
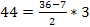
УСЛОВИЕ СБОРКИ

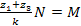
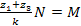
N, M – целые числа

k - число сателлитов планетарной передачи, выберем равное 3-м

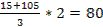
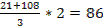
УСЛОВИЕ СОСЕДСТВА

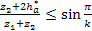
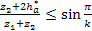
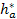= 1 – коэффициент высоты головки зуба

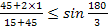
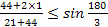
0,78 ≤ 0,87 0,71 ≤ 0,87