Табличный способ расчета сетевой модели
Дана сетевая модель, построенная по исходным данным, упрощенная и готовая к дальнейшему расчету табличным методом.
| |
Расчёты параметров модели ведутся по формулам и приведены в табл. 4.1. Для обозначения работ в формулах введём следующие индексы:
| h |
| i |
| j |
| k |
| thi |
| tij |
| tjk |
| Предш. работа |
| Данная работа |
| Послед. работа |
ij – шифр данной работы;
tij – срок выполнения данной работы;
hi – шифр предшествующей работы;
thi – продолжительность предшествующей работы;
jk – шифр последующей работы;
tjk – продолжительность последующей работы.
В состав рассчитываемых параметров сетевой модели входят: ранние характеристики работ (раннее начало, PHij, раннее окончание, POij); поздние характеристики работ (позднее начало, ПHij, позднее окончание, ПOij); резервы времени (общий Rij, частный rij).
Этапы расчета:
1 этап: заполняем первые 3 столбца таблицы сверху вниз (индексы последующих событий не должны опережать предшествующие). Работы выстраиваются в хронологическом порядке по начальному и конечному индексам.
Таблица 4.1.
Табличный способ расчета модели
| Шифр предш. Работы hi | Шифр данной работы ij | Про-должи-тель-ность данной работы tij | Раннее начало данной работы PHij | Ран- нее окон- чание рабо- ты POij | Позд- нее нача- ло ПНij | Позд- нее окон- ча- ние ПОij | Об- щий ре- зерв Rij Rij | Част- ный ре-зерв rij |
| 1-2 1-3 1-4 | 0 | 2(0+2) 3(0+3) 4(0+4) | ||||||
| 1-2 | 2-4 2-5 | 2(0+2) 5(2+3) | 6(6-0) 4(7-3) | |||||
| 1-3 | 3-4 3-6 | 3(0+3) 5(3+2) | 6(6-0) 3(5-2) | |||||
| 1-4, 2- 4, 3-4 | 4-7 | 4 max | 6(11-5) | |||||
| 2-5 | 5-7 5-8 | 11(11-0) 7(12-5) | ||||||
| 3-6 | 6-7 6-8 | 5(11-6) 8(12-4) | ||||||
| 4-7, 5-7, 6-7 | 7-8 | |||||||
2 этап: определяем ранние характеристики работ (сверху – вниз – гр. 4-5) по формулам с выражением данной работы через предшествующую.
Графа 4 PH (раннее начало) – самый ранний срок, в который может начинаться данная работа.
a) для работ, выходящих из исходного события, все ранние начала равны нулю РН 1-2;1-3;1-4 = 0; (4.1)
b) раннее окончание работы РОij = РНij + tij; (4.2)
c) для работ, выходящих из последующих событий и имеющих по одной предшествующей работе, РHij = РОhi; (4.3)
Для работ, выходящих из «сложного» события и имеющих несколько предшествующих работ.
| (4.4) |
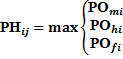
Примечание: максимальное из ранних окончаний работ (гр. 5) - критический путь сетевой модели (в данном случае он равен 12 дн.).
3 этап: определяем поздние характеристики работ (гр. 6, 7) – снизу вверх от завершающего события к исходному, выражая значения параметров через последующие работы:
a) поздние окончания всех работ, входящих в завершающее событие равны критическому пути ПО7-8,6-8,5-8 = Lкр; (4.5)
b) ПНij = ПОij - tij; (4.6)
c)
| (4.7) |
ПОij = ПНjk.
Для сложного события, из которого выходят несколько работ
| (4.8) |
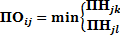
4 этап: находим резервы времени:
a)
| (4.9) |
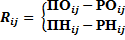
Работы с R = 0, лежат на критическом пути и r этих работ = 0.
b)
| (4.10) |
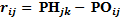
Работы, имеющие оба нулевых резерва, лежат на критическом пути.
5 этап: выделяем работы критического пути в таблице (R = 0, r = 0) и показываем их на сетевой модели жирной линией.
Контроль правильности расчета сетевой модели:
1) при расчете поздних начал для работ, выходящих из исходного события, должен получиться хотя бы один ноль.
2)
| (4.11) |
rij £ Rij
3) критический путь, построенный по работам с «0» резервами не должен прерываться.
Дата добавления: 2016-07-05; просмотров: 2699;











