Передача тепла теплопроводностью
Закон Фурье. Основным законом передачи тепла теплопроводностью является закон Фурье, согласно которому количество тепла 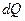 , передаваемого теплопроводностью, пропорционально градиенту температуры
, передаваемого теплопроводностью, пропорционально градиенту температуры 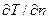 , времени
, времени 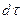 и площади сечения
и площади сечения 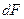 , перпендикулярного направлению теплового потока:
, перпендикулярного направлению теплового потока:
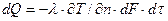 .
.
Коэффициент пропорциональности в этом уравнении называется коэффициентом теплопроводности. Этот коэффициент характеризует способность тел проводить тепло. Согласно уравнению теплопроводности, коэффициент имеет следующую размерность:
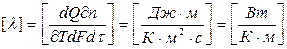 .
.
Коэффициент теплопроводности показывает, какое количество тепла проходит вследствие теплопроводности через 1 м2 поверхности в единицу времени при разности температур 1 К, приходящейся на 1 м длины нормали к изотермической поверхности.
Коэффициент теплопроводности веществ зависит от их природы и агрегатного состояния. Пределы изменения: для газов - 0,005–0,5; для жидкостей - 0,08–0,7; для металлов – 2,3–458; теплоизоляционных и строительных материалов – 0,02–3,0 Вт/(мК).
Для металлов, применяемых при изготовлении аппаратов пищевых производств, коэффициенты теплопроводности составляют: для нержавеющей стали – 14–23; свинца – 35; углеродистой стали – 45; чугуна – 63; алюминия – 204; меди – 384; серебра – 458 Вт/(мК).
Коэффициенты теплопроводности веществ зависят от температуры и давления. Для газов они возрастают с повышением температуры и мало зависят от давления. Для жидкостей с увеличением температуры уменьшаются, за исключением воды и глицерина. Теплопроводность твердых тел в большинстве случаев растет с повышением температуры.
Дифференциальное уравнение теплопроводности. Процесс распространения тепла теплопроводностью может быть описан дифференциальным уравнением, полученным на основе закона сохранения энергии, в предположении неизменности физических свойств тела по направлениям и во времени ( 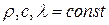 ).
).
Для вывода дифференциального уравнения рассматривается элементарный параллелепипед, выделенный из тела, с гранями 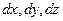 (рис. 3.1).
(рис. 3.1).
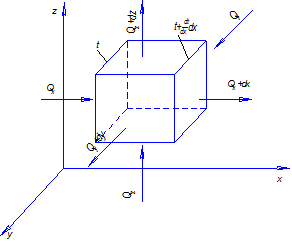
Рис. 3.1. Элементарный параллелепипед к выводу дифференциального уравнения
теплопроводности
Количество тепла, входящего в параллелепипед через грань в направлении оси 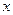 за время
за время 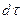 , по закону Фурье:
, по закону Фурье:
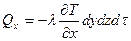 ,
,
выходящего через противоположную грань параллелепипеда:
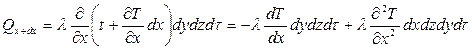 .
.
Разность между количеством тепла, вошедшего и вышедшего через грань в направлении оси 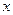 за время
за время 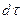 :
:
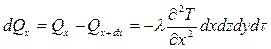 .
.
Для всех граней параллелепипеда:
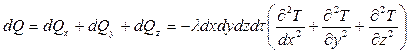 .
.
На основе закона сохранения энергии количество тепла 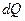 представляет тепло, которое идет на изменение энтальпии параллелепипеда за время
представляет тепло, которое идет на изменение энтальпии параллелепипеда за время 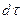 :
:
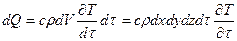 .
.
Сопоставив выражения для 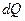 и произведя сокращения, получим дифференциальное уравнение теплопроводности
и произведя сокращения, получим дифференциальное уравнение теплопроводности
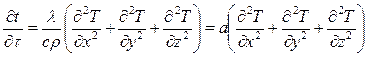
или в сокращенной записи:
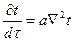 .
.
Множитель, входящий в уравнение теплопроводности 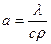 , называется коэффициентом температуропроводности. Этот коэффициент характеризует теплоинерционные свойства веществ: при прочих равных условиях быстрее нагревается или охлаждается то тело, которое обладает большим коэффициентом температуропроводности:
, называется коэффициентом температуропроводности. Этот коэффициент характеризует теплоинерционные свойства веществ: при прочих равных условиях быстрее нагревается или охлаждается то тело, которое обладает большим коэффициентом температуропроводности:
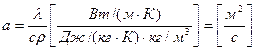 .
.
Уравнение позволяет решать задачи, связанные с распространением тепла теплопроводностью, как при неустановившихся, так и при установившихся тепловых потоках. При решении конкретных задач дифференциальное уравнение дополняется начальными и граничными условиями.
Теплопроводность плоской стенки. Рассмотрим передачу тепла теплопроводностью через плоскую стенку, длина и ширина которой бесконечно велики по сравнению с ее толщиной 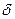 в направлении оси
в направлении оси 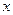 .
.
Температуры стенок равны 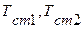 , причем
, причем 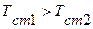 . При установившемся процессе количество тепла, подведенного к стенке и отведенного от нее, равны между собой и не изменяются во времени. В связи с тем, что температура меняется только в направлении оси
. При установившемся процессе количество тепла, подведенного к стенке и отведенного от нее, равны между собой и не изменяются во времени. В связи с тем, что температура меняется только в направлении оси 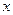 , дифференциальное уравнение одномерного температурного поля имеет вид:
, дифференциальное уравнение одномерного температурного поля имеет вид:
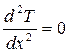 .
.
Интегрирование этого уравнения приводит к функции
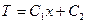 .
.
Константы интегрирования определяются исходя из следующих граничных условий:
при 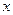 = 0 ,
= 0 , 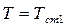 ,
,
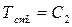 ;
;
при 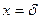 ,
, 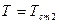 ,
,
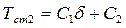
или 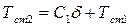 ,
,
откуда 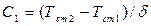 .
.
Подставив значения констант 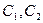 в уравнение, получим
в уравнение, получим
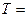
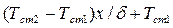 .
.
Тогда для температурного градиента:
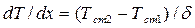 .
.
После подстановки выражения для температурного градиента в уравнение теплопроводности получим для количества тепла
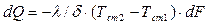
или
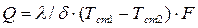 .
.
Если плоская стенка состоит из 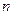 слоев, отличающихся друг от друга теплопроводностью и толщиной, то при установившемся процессе через каждый слой стенки пройдет одно и то же количество тепла, которое может быть выражено для различных слоев уравнениями:
слоев, отличающихся друг от друга теплопроводностью и толщиной, то при установившемся процессе через каждый слой стенки пройдет одно и то же количество тепла, которое может быть выражено для различных слоев уравнениями:
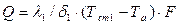 или
или 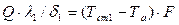
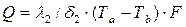 или
или 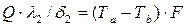
…………………………………………………..
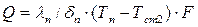 или
или 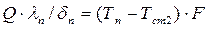
Произведем сложение правых и левых частей этих уравнений. В результате получим
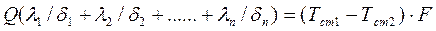 ,
,
откуда
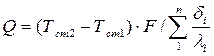 .
.
Зависимости для расчета теплового потока через однослойную и многослойную цилиндрические стенки приведем без вывода:
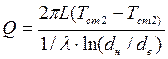 ;
;
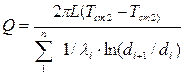 .
.
При 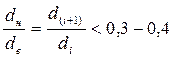 расчет теплового потока можно вести как для плоской стенки.
расчет теплового потока можно вести как для плоской стенки.
Тепловое излучение
Если на поверхность тела попадает лучистая энергия в количестве 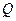 , то в общем случае телом поглощается только часть ее
, то в общем случае телом поглощается только часть ее 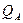 с последующим превращением в тепловую энергию. Часть лучистой энергии
с последующим превращением в тепловую энергию. Часть лучистой энергии 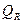 отражается от поверхности тела, а часть
отражается от поверхности тела, а часть 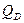 проходит сквозь него. Очевидно, что
проходит сквозь него. Очевидно, что
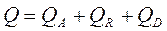 ;
;
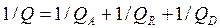 .
.
Первое слагаемое равенства характеризует поглощательную способность тела, второе – отражательную, третье – пропускательную.
В пределе каждое из слагаемых может быть равно единице, если каждое из оставшихся двух равно нулю.
При 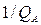 =1 и соответственно
=1 и соответственно 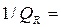 0 и
0 и 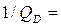 0 тело полностью поглощает все падающие на него лучи. Такие тела называются абсолютно черными.
0 тело полностью поглощает все падающие на него лучи. Такие тела называются абсолютно черными.
При 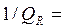 1,
1, 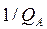 = 0 и
= 0 и 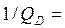 0 тело отражает все падающие на него лучи. Такие тела называются абсолютно белыми.
0 тело отражает все падающие на него лучи. Такие тела называются абсолютно белыми.
При 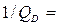 0,
0, 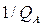 =0 и
=0 и 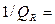 0 тело пропускает все падающие лучи. Такие тела называются абсолютно прозрачными или диатермичными.
0 тело пропускает все падающие лучи. Такие тела называются абсолютно прозрачными или диатермичными.
Тела, которые поглощают, отражают и пропускают ту или иную часть падающих на них лучей, называются серыми телами.
Закон Стефана – Больцмана. Количество тепла, излучаемого единицей поверхности тела в единицу времени, называется лучеиспускательной способностью тела:
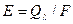 .
.
Лучеиспускательная способность, отнесенная к длинам волн от 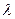 до
до 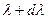 , т.е. к интервалу волн
, т.е. к интервалу волн 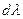 , называется интенсивностью излучения:
, называется интенсивностью излучения:
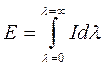
 .
.
Планком теоретически получена следующая зависимость общей энергии теплового излучения от абсолютной температуры и длин волн для абсолютно черного тела:
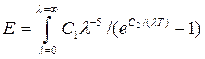 ,
,
входящие в уравнение константы: 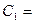 3,22∙10-16 Вт/м2, С2 = 1.24∙10-2 Вт/м2.
3,22∙10-16 Вт/м2, С2 = 1.24∙10-2 Вт/м2.
Это уравнение после разложения знаменателя в ряд и последующего интегрирования позволяет выразить полную энергию, или лучеиспускательную способность абсолютно черного тела:
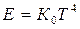 .
.
Константа лучеиспускания абсолютно черного тела 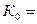 5,67∙10-8 Вт/(м2К4).
5,67∙10-8 Вт/(м2К4).
Уравнение носит название закона Стефана – Больцмана, согласно которому лучеиспускательная способность абсолютно черного тела пропорциональна четвертой степени абсолютной температуры его поверхности.
При проведении технических расчетов приведенную зависимость для удобства используют в несколько ином виде:
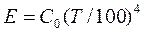 ,
,
где 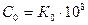 Вт/(м2К4) – коэффициент лучеиспускания абсолютно черного тела.
Вт/(м2К4) – коэффициент лучеиспускания абсолютно черного тела.
Закон Стефана – Больцмана применим также к серым телам:
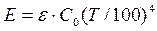 ,
,
где 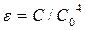 - относительный коэффициент лучеиспускания, или степень черноты серого тела;
- относительный коэффициент лучеиспускания, или степень черноты серого тела; 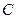 – коэффициент лучеиспускания серого тела.
– коэффициент лучеиспускания серого тела.
Значение 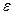 всегда меньше единицы и колеблется в пределах от 0,055 для алюминия, до 0,95 для твердой резины. Для листовой углеродистой стали
всегда меньше единицы и колеблется в пределах от 0,055 для алюминия, до 0,95 для твердой резины. Для листовой углеродистой стали 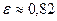 при температуре окружающей среды.
при температуре окружающей среды.
Закон Кирхгофа. Для серых тел необходимо знать зависимость между их излучательной и поглощательной способностью.
Рассмотрим (рис. 3.2) серое и абсолютно черное тела, расположенные параллельно друг другу.
Примем, что все лучи, испускаемые поверхностью одного тела, падают на поверхность другого. Абсолютно черное тело имеет температуру 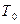 , лучеиспускательную способность
, лучеиспускательную способность 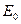 и поглощательную
и поглощательную 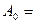 1, серое тело соответственно
1, серое тело соответственно 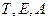 , при этом
, при этом 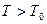 . Излучение
. Излучение 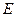 попадает на абсолютно черное тело и целиком поглощается им. Излучение
попадает на абсолютно черное тело и целиком поглощается им. Излучение 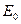 попадает на серое тело, при этом часть его, равная
попадает на серое тело, при этом часть его, равная 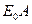 , поглощается, а другая часть, равная
, поглощается, а другая часть, равная 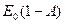 , отражается на абсолютно черное тело и поглощается им. Таким образом, в результате лучистого теплообмена между телами абсолютно черное тело получает суммарное количество энергии:
, отражается на абсолютно черное тело и поглощается им. Таким образом, в результате лучистого теплообмена между телами абсолютно черное тело получает суммарное количество энергии:
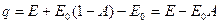 .
.
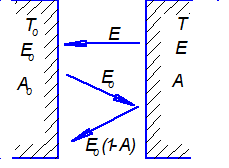
Рис. 3.2. Лучистый теплообмен с параллельно расположенными поверхностями
Если обмен лучистой энергией между телами происходит при одинаковых температурах 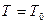 , то количество энергии, переданной от одного тела к другому, равно нулю и, следовательно:
, то количество энергии, переданной от одного тела к другому, равно нулю и, следовательно:
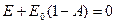 ,
, 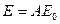 и
и 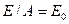 .
.
Полученное равенство является математическим выражением закона Кирхгофа, согласно которому отношение лучеиспускательной способности тел к их поглощательной способности для всех тел одинаково, равно лучеиспускательной способности абсолютно черного тела при той же температуре и зависит только от температуры.
Взаимное излучение двух твердых тел. Количество тепла, передаваемое излучением от более нагретого твердого тела менее нагретому, определяется по уравнению
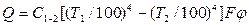 ,
,
где коэффициент взаимного излучения 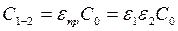 ;
; 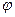 – средний угловой коэффициент, определяется формой, размерами и взаимным расположением поверхностей, участвующих в теплообмене;
– средний угловой коэффициент, определяется формой, размерами и взаимным расположением поверхностей, участвующих в теплообмене; 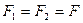 - излучающая поверхность тел.
- излучающая поверхность тел.
Значения коэффициента приводятся в специальной литературе. Если одно тело находится внутри другого, то 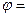 1. В этом случае коэффициент взаимного излучения определяется в соответствии с уравнением
1. В этом случае коэффициент взаимного излучения определяется в соответствии с уравнением
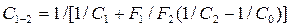 .
.
В этом уравнении индекс «1» соответствует более нагретому телу, расположенному внутри другого.
Если поверхности равны и параллельны, то в соответствии с приведенным выше выражением
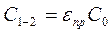 .
.
Для более нагретого тела с поверхностью 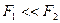 из того же выражения следует
из того же выражения следует
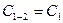 .
.
Для того, чтобы уменьшить лучистый теплообмен между телами или организовать защиту от вредного влияния сильного излучения, используют перегородки – экраны, изготовленные из хорошо отражающих лучи материалов. Экраны располагают между поверхностями, обменивающимися лучистой энергией.
Дата добавления: 2016-06-29; просмотров: 3739;











