Применение метода моделирования для исследования и расчета процессов и аппаратов пищевых производств
Изучение процессов с целью получения уравнений, необходимых для их анализа и расчета, можно проводить теоретически. Это наиболее желательный путь решения той или иной инженерной задачи. Он сводится к составлению на основе общих законов физики и химии и решению математических зависимостей, чаще всего дифференциальных уравнений, в полной мере описывающих процесс.
Дифференциальные уравнения описывают целый класс однородных по своей сущности явлений (например, класс явлений распространения тепла теплопроводностью), и для выделения из него конкретного явления необходимо ограничить указанные уравнения дополнительными условиями. Инженера интересует конкретное явление данного класса, наблюдаемое в условиях работы определенного аппарата. Поэтому из множества возможных решений исходного уравнения (или системы уравнений) надо выбрать одно решение, соответствующее исследуемому явлению, т.е. получить однозначное решение. Для этого в имеющиеся условия задачи вводят дополнительные, называемые условиями однозначности и не содержащиеся в исходной системе уравнений. Эти условия ограничивают решение дифференциальных уравнений единственным конкретным случаем.
Условия однозначности включают:
а) данные о геометрических свойствах системы (конфигурации и размерах аппарата);
б) сведения о физических свойствах продуктов (плотности, теплопроводности, вязкости и т.п.);
в) данные о состоянии системы на границе (граничные условия) и о взаимодействии с окружающей средой (распределение температур, давлений, концентраций на поверхности, интенсивность теплоотдачи или массоотдачи и др.);
г) данные о состоянии системы в начальный и конечный моменты времени (временные условия).
Таким образом, дифференциальные уравнения должны решаться совместно с условиями однозначности в устанавливаемых ими пределах.
Однако многие процессы пищевой технологии характеризуются большим числом переменных и настолько сложны, что зачастую удается дать только математическую формулировку задачи и установить условия однозначности. Полученные же дифференциальные уравнения не могут быть решены известными в математике методами. Больше того, некоторые процессы, имеющие место в технологической аппаратуре, настолько сложны, что даже нельзя составить систему дифференциальных уравнений, достаточно полно описывающую данный процесс.
Таким образом, теоретический вывод расчетных зависимостей, необходимых для проектирования аппаратуры, зачастую оказывается невозможным. Поэтому для нахождения связи между величинами, характеризующими процесс, прибегают к экспериментальному исследованию, т.е. к проведению опытов.
На основе опытных данных можно получить эмпирические уравнения, которые носят частный характер и не могут быть распространены на условия, отличные от тех, для которых они получены. Такие уравнения не представляют большой ценности и находят ограниченное распространение в инженерной практике.
Наиболее целесообразно проводить и обрабатывать эксперименты таким образом, чтобы появлялась возможность обобщения результатов опыта, распространения их на широкий круг явлений, подобных исследованному, но отличающихся численными значениями характерных параметров, например, размерами аппаратов, физическими свойствами сред и т.д. Хорошие результаты при обобщении опытов достигаются использованием методов теории подобия.
Теория подобия является учением о методах научного обобщения эксперимента. Она дает информацию о том, как надо ставить опыты и обрабатывать результаты, чтобы при проведении даже небольшого числа экспериментов иметь возможность обобщать опытные данные, получая единые уравнения для всех подобных явлений. Применение теории подобия зачастую позволяет вместо дорогостоящих трудоемких опытов на промышленной аппаратуре выполнять исследования на моделях значительно меньшего размера, и, что немаловажно, проводить опыты не с рабочими веществами и не в жестких условиях технологического регламента, а с другими (модельными) веществами в условиях, отличающихся от промышленных.
Таким образом, методы теории подобия лежат в основе масштабирования и моделирования процессов.
Моделированием называется метод изучения существующего или создаваемого объекта, при котором вместо реального объекта изучается модель (другой объект меньшего размера), а полученные количественные результаты распространяются на реальный объект. Основной результат моделирования заключается в предсказании поведения реального объекта в рабочих условиях производства на основании расчета необходимых параметров оригинала по измеренным параметрам модели.
Методы моделирования основаны на подобии различных объектов. Подобными называются такие объекты, у которых соответствующие параметры, определяющие состояние объектов в пространстве и времени, отличаются только масштабом физических величин.
Модели делятся на знаковые (символические, мысленные) и реальные (вещественные, материальные).
Знаковые модели состоят из математических зависимостей, связывающих физико-химические, режимные и конструктивные параметры технологического процесса, отражающие в явной форме физическую сущность этого процесса. Такие модели содержат математическое описание процесса и называются математическими. Выбор способа описания (теория вероятностей, дифференциальные, интегральные и другие уравнения) определяются характером и сложностью изучаемой системы.
Математическому моделированию обязательно предшествует тщательное всестороннее изучение сущности процесса.
Важной особенностью мысленных моделей является возможность описывать объект различными способами и с разной степенью упрощения. Во многих случаях целесообразно использование самых простых моделей (например, в термодинамике модель идеального газа для приближенного описания свойств реальных газов).
Математическое описание процессов практически реализуется составлением алгоритмов, с помощью которых на ЭВМ получают численные характеристики процессов. Варьируя исходные данные, переменные, влияющие на процесс, путем замены реального объекта математической моделью, с помощью численного эксперимента удаётся установить оптимальные условия проведения процесса. Получив решение, необходимо выявить его соответствие изучаемому объекту, проверить модель на адекватность.
Реальная (материальная) модель является физическим объектом, выполненным в металле, оснащенным приборами, снабженным рабочим (исследуемым) веществом и т.п.
Реальные модели подразделяются на физические и аналоговые.
Физическая реальная модель имеет одинаковую с изучаемым объектом физическую природу и воспроизводит его свойства. Например, гидродинамический процесс перемешивания в промышленной мешалке можно моделировать в лабораторной мешалке меньшего размера с применением другой «модельной» жидкости.
Аналоговая реальная модель основана на сходстве математического описания процессов различной физической природы и воспроизводит аналогию между законами, которые выражают сходные явления в реальном объекте и модели. Например, существует аналогия между законами переноса тепла, вещества, количества движения, фильтрацией жидкости через пористое тело, прохождением электрического тока и другими законами. Поэтому при определенных условиях возможен единый подход к разным по физической природе явлениям.
Рассмотрим различные по физической природе явления и их математические описания:
а) закон теплопроводности Фурье
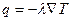 ;
;
б) закон молекулярной диффузии Фика (перенос вещества)
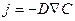 ;
;
в) закон внутреннего трения
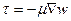 ;
;
г) закон Ома (перенос электричества)
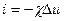 ;
;
д) закон фильтрации Дарси – Вейсбаха
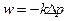 .
.
Все представленные дифференциальные уравнения изоморфны, т.е имеют идентичную, одинаковую по форме математическую запись.
В уравнения входят:
- соответствующие градиенты: температуры 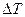 , К/м; концентрации
, К/м; концентрации 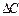 , кг/м4; скорости
, кг/м4; скорости 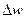 , 1/с; электрического потенциала
, 1/с; электрического потенциала 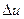 , В/м: давления
, В/м: давления 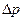 , Н/м2;
, Н/м2;
- соответствующие плотности потоков: тепла 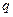 , Вт/м2; вещества
, Вт/м2; вещества 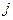 , кг/(м2с); количества движения
, кг/(м2с); количества движения 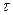 , Н/м2; электричества
, Н/м2; электричества 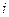 , А/ м2; жидкости
, А/ м2; жидкости 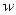 , м/( с·м2).
, м/( с·м2).
Коэффициентами пропорциональности между плотностями потоков и градиентами служат соответственно коэффициенты: теплопроводности 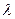 , Вт/(м·К); диффузии
, Вт/(м·К); диффузии 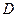 , м2/с; вязкости
, м2/с; вязкости 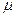 , Н·с/ м2; удельной проводимости
, Н·с/ м2; удельной проводимости 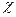 , А/(В·м); фильтрации
, А/(В·м); фильтрации 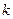 , Н·с/ м2.
, Н·с/ м2.
Любой из указанных законов с введением размерных коэффициентов пропорциональности можно представить, например, на электрической модели как закон Ома, на гидравлической модели как закон течения жидкости и т.д. Так появились аналогии: электротепловая – ЭТА; электрогидродинамическая – ЭГДА и др.
В пищевой технологии, как уже было отмечено, с моделированием чаще всего связывают экспериментальный метод, основанный на проведении опытов на физических материальных моделях с распространением результатов на реальный объект. Нередко при проведении заводских опытов моделью служит сам промышленный аппарат, что облегчает задачу масштабного перехода от модели к объекту. Однако в этом случае возможности варьирования параметров процесса ограничены и основаны лишь на наблюдаемых в промышленном процессе факторах. При таком экспериментальном исследовании могут выпасть из поля зрения некоторые факторы, действие которых может не проявляться в условиях наблюдаемого процесса.
Дата добавления: 2016-06-29; просмотров: 2627;











