ИССЛЕДОВАНИЕ АКТИВНОГО ФИЛЬТРА НА ОПЕРАЦИОННОМ УСИЛИТЕЛЕ (ОУ)

Фильтр, состоящий из пассивных RC элементов на базе ОУ (активного элемента), называется активным фильтром. В этом случае ОУ охватывается отрицательной обратной связью (ООС). Принцип ООС заключается в том, что часть выходного сигнала через цепь обратной связи передается на вход и вычитается из выходного сигнала. Из рис. 6.1 видно, что

.

Т.к. А_D = 10⁴ ÷ 10⁵, то значением 1/ А_D можно пренебречь.

А – коэффициент усиления ОУ, охваченного ООС.

А_D – коэффициент усиления собственно ОУ.

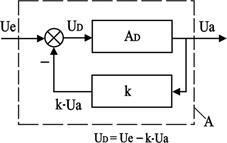
Коэффициент усиления ОУ, охваченного ООС, не зависит от коэффициента, т.е. не зависит от параметров собственно ОУ, а определяется только параметрами ООС.

При решении схемотехнических задач с использованием операционного усилителя, охваченного ООС, необходимо помнить:

1. Так как при наличии ООС (рис. 6.1) представляет малую величину, то ею можно пренебречь. Иными словами, в режиме ООС разность напряжений между входами стремится к нулю .

2. Входы ОУ имеют большое входное сопротивление, входной ток не превышает нескольких нА и им можно пренебречь. Т.е. можно принять, что при любых схемах включения входной ток ОУ равен нулю.

В лабораторной работе рассматриваются активные фильтры второго порядка. Передаточные функции этих фильтров могут представлять собой комбинации типовых звеньев.

1. Усилительное звено с коэффициентом усиления k = α.

2. Дифференцирующее звено 1-го порядка. Его каноническая передаточная функция

.

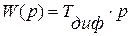При гармоническом сигнале

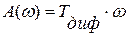(6.1)

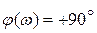, (6.2)

где ω – круговая частота, 1/с;

А – отношение амплитуд выхода и входа;

φ – сдвиг фазы.

3. Колебательное звено 2-го порядка. Его каноническая передаточная функция

,

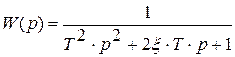где ξ - коэффициент демпфирования.

Знаменатель – не что иное, как характеристическое уравнение дифференциального линейного уравнения. Если корни характеристического уравнения комплексные сопряженные, то решения дифференциального уравнения содержат гармонические составляющие. Корни комплексные, если ξ < 1

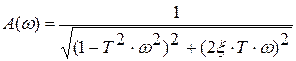, (6.3)

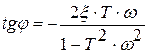. (6.4)

Анализируя выражения (6.3) и (6.4), можно сделать следующие выводы.

1. На низких частотах (ω→ 0) .

Падение амплитуды становится заметным при ω > 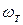= 1/T.

2. Если ω = = 1/T , то

, (6.5)

. (6.6)

3. Если продифференцировать (6.3), приравнять к нулю и решить относительно , то получим выражение для резонансной частоты

, (6.7)

. (6.8)

Из выражения (6.7) видно, что чем больше ξ , тем меньше .

Учитывая, что - есть действительная положительная величина, то это выражение имеет смысл только в том случае , если (1 – 2∙ξ ) > 0 или

. Это есть условие появления резонанса.

4. Если имеет место резонанс ( 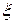< 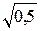) , то на определенной частоте значение 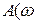) достигнет единицы. Эта частота называется частотой среза ( ). Поэтому, приравнивая (6.3) единице и решая относительно 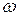, получим

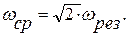(6.9)

Амплитудные значения типовых звеньев следует перемножать, фазовые значения следует алгебраически складывать.

На рис. 6.3 изображен активный фильтр нижних частот второго порядка и его передаточная функция. На рис. 6.3 изображен активный фильтр верхних частот второго порядка и его передаточная функция. Передаточные функции приведены к канонической форме.

ЛИТЕРАТУРА

а) Основная литература:

· Лачин В. И. Савелов Н.С. Электроника: учебное пособие для ВТУЗов. — Ростов н/Д: Феникс, 2005

б) Дополнительная литература:

· Витвицкий В.П., Кривенцев В.И. Авиационная электроника. Ч.I. Аналоговые электронные устройства авиационной автоматики. - М.: МГТУ ГА, 2002

· Витвицкий В.П., Кривенцев В.И. Авиационная электроника. Ч.II. Цифровые электронные устройства авиационной автоматики. - М: МГТУ ГА, 2002

· Рекус Г.П. Сборник задач и упражнений по электротехнике и основам электроники. М.: Высшая школа. 2001

· Лашин В.Ю., Майская Е.Р. Электротехника и электроника. Пособие по выполнению лабораторных работ. - МГТУ ГА, 2011

· А.А. Савелов А.Т. Трубачев. Основы электроники. Пособие по выполнению курсовой работы для студентов направления 162500 всех форм обучения. - М.: МГТУ ГА, 2012

· Карлащук В.И. Электронная лаборатория на IBM PC. Программа Electronics Workbench и ее применение. Изд. “Солон-Р”, Москва, 1999 г.

· Григорьев О.П., Замятин В.Я. и др. Транзисторы. Справочник. М.:Радио и связь, 1989 г.

·

Приложение