Построение множества оптимальных по Парето альтернатив

Наличие нескольких критериев задает на множестве альтернатив частичное упорядочение. Подозрительными на наилучшее соответствие цели проектирования являются максимальные по этому упорядочениюальтернативы. Поясним сказанное.

Предположим, что мы должны сделать выбор на допустимом множестве альтернатив G_x, так, чтобы

f₁( ) → max, …, f_r( ) → max.

Допустим, мы сделали некоторый выбор. Обозначим его 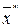и предположим, что существует некоторый другой выбор 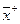, такой, что для всех критериев f_i( 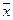) имеет место неравенство:

f_i ( 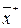) ≥ f_i( 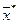), i = 1, 2,…, r, (6.11)

причем, хотя бы одно неравенство – строгое.

Очевидно, что выбор 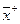предпочтительнее 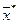. Поэтому все векторы 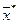, удовлетворяющие(6.11), следует исключить из рассмотрения. Имеет смысл заниматься сопоставлением, подвергать неформальному анализу только те векторы 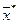, для которых не существует 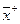такого, что для всех критериев удовлетворяются неравенства (6.11). Множество всех таких векторов 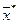называют множеством Парето, а вектор 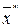называют не улучшаемым вектором результатов (оптимальный по Парето), если f_i( 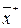) ≥ f_i( 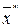) для любого i следует f_i( 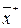) = f_i ( 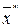). Очевидно, что векторы множества Парето являются максимальными по частичному упорядочению, заданному критериями f_i( ), i = 1, 2,…, r. Оптимальность по Парето означает, что нельзя дальше улучшить значение одного из частных критериев, не ухудшая при этом значение хотя бы одного из остальных. Применительно к поведению людей суть дела ясно выразил японскийученыйНикайдо: предпочтительнее поведение, при котором одному (неважно, кому именно) становится лучше, если никому другому не становится при этом хуже.

В теории принятиярешений существует термин «принцип Парето», заключающийся в том, что выбирать в качестве решения следует только тот вектор 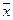, который принадлежит множеству Парето. Принцип Парето не выделяет единственного решения, он только сужает множество альтернатив. Окончательный выбор остается за лицом, принимающим решение. Но исследователь, построив множество Парето, облегчает процедуру выбора решения. Таким образом, возникает задача построения множества Парето.

Приближенное построение множества Парето относится к числу очень важных и трудных задач численного анализа. Рассмотрим несколько простых примеров, поясняющих процесс построения множества Парето. Пустьрешается задача:

f₁( ) → max , f₂( 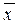) → ma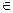x, G_x.

Каждой точке 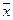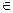G_xсоотношения f₁ = f₁( ), f₂ = f₂( ) ставят в соответствие некоторую точку 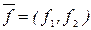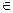Е в плоскости критериев и определяют отображение G_x на G_F(рис. 6.2).

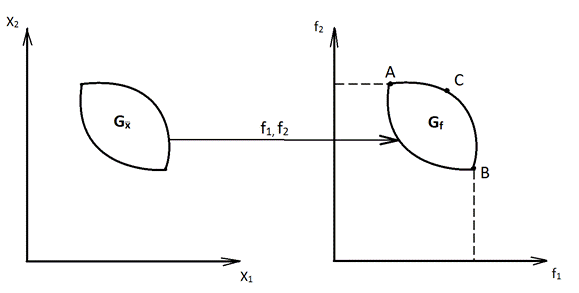
Рис. 6.2

Множество G_Fносит название множества достижимости или множества предельных возможностей,или пространства критериев. Изучение структуры этого множества может оказаться весьма полезным при исследовании различных задач проектирования.Заметим, что образ множества Парето в множестве G_F представляет собой лишь часть множества G_F (на рис. 6.2 – дуга АСВ).

Приближенное построение образа множества Парето сводится к последовательному решению ряда задач математического программирования. Опишем две из возможных схем расчета. Фиксируем некоторое желательное значение критериев f₁ и f₂; f₁ = С₁, f₂ = С₂. Значения С₁ и С₂ следует выбрать так, чтобы они принадлежали множеству достижимости. Далее решаются две оптимизационные задачи:

I. f₁( ) → max II. f₂( ) → max

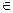G_x, f₂( ) = С₂ 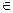G_x, f₁( ) = С₁.

Решив эти задачи, мы определим точки А и В в множестве достижимости. Проведя черезних прямую, получим простейшую аппроксимацию образа множества Парето в множестве G_F.

Для уточнения аппроксимации решаются следующие задачи:

III. f₁( ) → max IV. f₂( ) → max

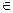G_x, f₂( 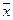) = С₄ 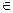G_x, f₁( ) = С₃

Находим еще две точки – C и D. Через точки А, С, D, В (рис. 6.3) проведем ломаную, которая и будет следующим приближением образа множества Парето. Данная процедура может быть продолжена.

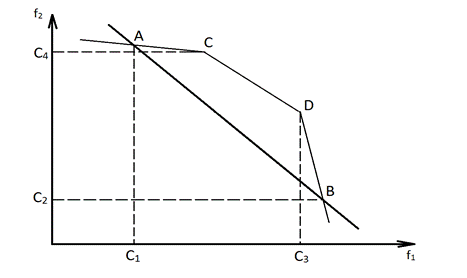
Рис. 6.3

Очень часто подобной информации о структуре образа множества Парето уже бывает достаточно для решения практических задач.

Другой способ приближенного построения образа множества Парето. Пусть λ_i, i = 1, 2, ..., r – неотрицательные числа, такие, что 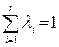. Составим новый критерий:

и решим следующую задачу:

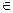F( ) → max, G_x.

Оказывается, что решение этой задачи определяет такой вектор 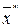, что точка с координатами (f₁( 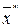), f₂( 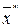), …, f_r( 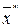)) принадлежит образу множества Парето. Поэтому, варьируя значения коэффициентов λ_i можно получить любое количество точек образа множества Парето. Следовательно, как и в предыдущем случае, можно построить ломаную, являющуюся приближением образа множества Парето в пространстве F. При этом соответствующие описанные способы можно распространить и на случай большего числа критериев.

Если образ множества Парето выпуклый, то, увеличивая количество точек, которые определяются одним из описанных выше способов, можно построить ломаную (или многогранник для большего числа критериев), аппроксимирующую это множество с любой степенью точности. Но, к сожалению, практика дает примеры множеств Парето, которые не являются выпуклыми. Тогда задача их аппроксимации резко усложняется.

Подведем итог. В результате полного использования всей информации, заложенной в формальной постановке задачи, получается множество не сравнимых между собой альтернатив (множество Парето или множество компромиссов, или множество не улучшаемых точек, или эффективное множество). Следовательно, выделение множества Парето не решает поставленной задачи. Однако благодаря этой процедуре, во-первых, сужается множество исходных вариантов, во-вторых, анализ множества Парето может подтолкнуть проектировщика (ЛПР) к дополнительной информации о своих предпочтениях.

Область Парето содержит, как правило, очень много элементов, в связи с чем возникает необходимость в дальнейшем сужении этой области. Эта проблема является одной из основных проблем в задачах многокритериальной оптимизации. Как правило, выбор оптимальных по Парето решений возможен лишь за счет привлечения дополнительной информации о предпочтениях ЛПР. Одним из наиболее распространенных видов дополнительной информации является информация об относительной важности критериев. Смысл данной информации состоит в том, что критериям приписываются некоторые коэффициенты (веса), определяющие важность критериев. К данному времени разработаны многочисленные процедуры по назначению коэффициентов и дальнейшему их использованию . Но, как правило, эти методы являются эвристическими и не содержат в своей основе строгой доказательной базы. Последнее обстоятельство приводит к тому, что результат задачи зависит от выбора той или иной процедуры. Другая проблема, связанная с первой, заключается в том, что принцип Парето «работает» только в определенном классе задач. Если поведение ЛПР выходит за рамки этого класса, то наилучшее решение необязательно будет оптимальным по Парето.

Окончательный выбор оптимального решения из множества Парето остается за ЛПР. В частности, для этого можно использовать, например, три типа процедур решения многокритериальных задач, которые были указаны при их классификации.