Момент тангажа крыла

Для сравнения характеристик продольной устойчивости и управляемости самолетов с различными крыльями используется понятие средней аэродинамической хорды (САХ).

За САХ крыла произвольной формы в плане принимается хорда эквивалентного прямоугольного крыла, у которого площадь 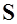, полная аэродинамическая сила 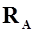и аэродинамический момент тангажа 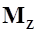от этой силы такие же, как и у действительного крыла.

Введем базовую систему координат 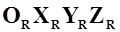, относительно плоскости 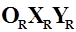которой большинство элементов самолета расположены симметрично слева и справа. Начало базовой системы координат расположено в носке центральной хорды крыла. Величина САХ 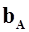представляет собой отрезок, параллельный базовой плоскости самолета 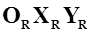и определяется по соотношению [1].

Определив 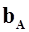и координаты носка САХ в базовой системе координат, можно заменить действительное крыло эквивалентным прямоугольным крылом и для него найти .

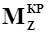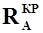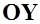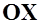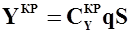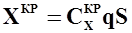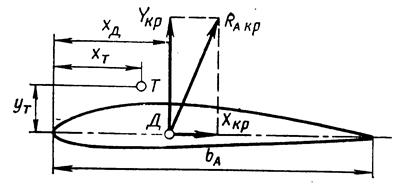
В результате обтекания потоком воздуха крыла возникает полная аэродинамическая сила , приложенная в центре давления. Проектируя эту силу на оси и связанной системы координат, получим нормальную и продольную аэродинамические силы. Определим момент этих сил относительно поперечной оси 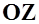, проходящей через центр масс самолета с координатам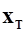и и 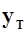(рис. 1):

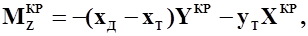(2.5)

где 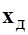- координата центра давления.

Рис. 1. Центр давления и силы, действующие на крыло в полете

Наиболее распространено определение момента тангажа с использованием понятия фокуса по углу атаки.

Фокусом по углу атаки называется точка, расположенная по линии пересечения плоскости 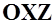связанной системы координат с плоскостью симметрии самолета 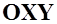, относительно которой момент тангажа остается постоянным при малых изменениях только угла атаки.

Можно определить фокус по углу атаки также как точку приложения приращения аэродинамической силы 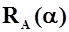, вызванной изменением только угла атаки от 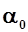до .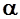

Используя понятие фокуса представим 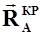в виде двух составляющих: 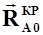при 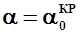- независящую от изменения 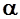и приложенную в центре давления 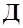и 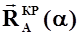- зависящую от изменения угла атаки от 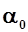до 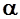и приложенную в фокусе крыла 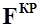. Проекцию 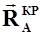на ось 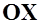(т.е. силу 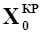) перенесем по линии ее действия в фокус крыла. Тогда в фокусе будет приложена продольная сила 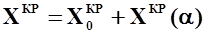(рис. 2).

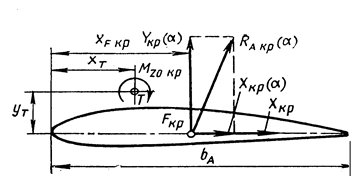
Рис. 2. Определение аэродинамического момента тангажа крыла с использованием фокуса по углу атаки

Из рисунка видно, что аэродинамический момент тангажа крыла относительно оси 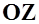, проходящей через точку 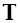равен

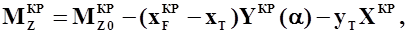(2.6)

где 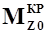- момент тангажа при 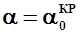, т.е. при нулевой подъемной силе;

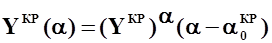- подъемная сила крыла;

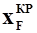- координата фокуса крыла - расстояние от носка САХ до фокуса .

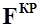Здесь и в дальнейшем верхний индекс за скобками означает частную производную величины, стоящей в скобках, по этому индексу.

Вводя безразмерный коэффициент аэродинамического момента тангажа 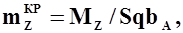получим

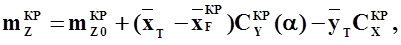(2.7)

где 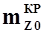- коэф­фициент аэродинамического момента тангажа крыла при нулевой подъемной силе;

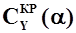- приращение коэффициента нормальной силы крыла при изменении угла атаки от 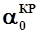до ;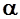

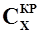- коэффициент аэродинамической продольной силы крыла;

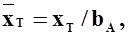
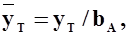
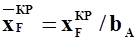- относительные координаты центра масс самолета и фокуса крыла.

Отметим, что при 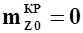(симметричные профили и отсутствие совместного влияния крутки и стреловидности крыла) фокус крыла 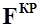совпадает с центром давления 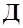. Когда 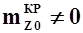, центр давления не совпадает с фокусом и перемещается по САХ при изменении угла атаки.

При небольших углах атаки 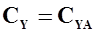. Тогда

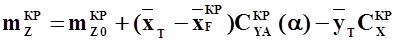, (2.8)

где 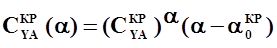- приращение коэффициента аэродинамической подъ­емной силы крыла при изменении угла атаки от 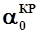(когда 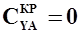) до ;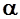

.

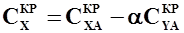Если 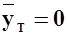, то .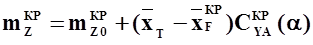

Величины 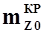и 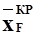зависят от формы крыла в плане, его профиля, крутки и т.п., а также от числа 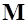полета. На дозвуковых скоростях 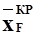= 0,2...0,3, а на сверхзвуковых скоростях фокус смещается назад и 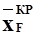= 0,4..,0,5.