Критерий Коши сходимости ряда.
Необходимый признак сходимости числового ряда.
С бесконечным рядом (1) связаны ряды вида 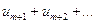 , называемые остатками ряда (обозначается
, называемые остатками ряда (обозначается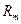 ).Справедливо следующее утверждение.
).Справедливо следующее утверждение.
Утверждение 1. Числовой ряд (1) сходится тогда и только тогда, когда для любого 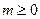 сходится его остаток
сходится его остаток 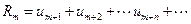 .
.
Доказательство.
Достаточность. Если для любого 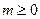 остаток
остаток 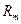 сходится, то он сходится и при
сходится, то он сходится и при 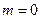 . Но
. Но 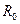 – это и есть исходный ряд.
– это и есть исходный ряд.
Необходимость. Если ряд (1) сходится, то существует 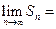
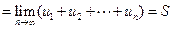 . Но
. Но 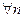 частичная сумма
частичная сумма 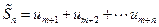 ряда
ряда 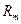 имеет вид
имеет вид 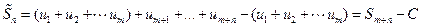 . Величина
. Величина 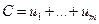 не зависит от
не зависит от 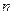 . Кроме того,
. Кроме того, 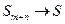 при
при 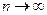 . Поэтому существует
. Поэтому существует 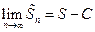 . Утверждение доказано.
. Утверждение доказано.
Итак, исследование сходимости ряда и исследование сходимости любого его остатка – эквивалентные задачи. Значит, при изучении сходимости ряда можно рассматривать его, начиная с некоторого номера. Это не влияет на сходимость ряда, изменится лишь его сумма.
Напомним формулировку критерия Коши для числовых последовательностей:
последовательность 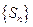 сходится тогда и только тогда, когда
сходится тогда и только тогда, когда
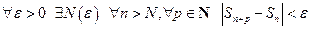 .
.
Здесь 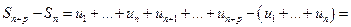
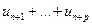 . Так как сходимость последовательности частичных сумм означает сходимость ряда, то сформулируем критерий Коши для рядов.
. Так как сходимость последовательности частичных сумм означает сходимость ряда, то сформулируем критерий Коши для рядов.
Теорема. Числовой ряд (1) сходится тогда и только тогда, когда
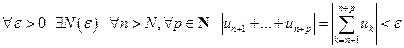 .
.
Следствие. (Необходимый признак сходимости ряда). Если числовой ряд сходится, то его общий член стремится к нулю: 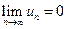 .
.
Действительно, из критерия Коши при 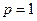 получаем неравенство
получаем неравенство 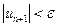 , выполняющееся
, выполняющееся 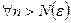 . Это и значит, что
. Это и значит, что 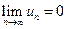 .
.
Следует отметить, что этот признак является лишь необходимым, но не достаточным признаком сходимости ряда. Можно указать расходящийся ряд, для которого выполняется условие 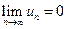 . Например, для гармонического ряда
. Например, для гармонического ряда 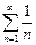 очевидно справедливо равенство
очевидно справедливо равенство 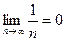 , т.е. общий член ряда стремится к нулю, но как мы видели выше, этот ряд расходится.
, т.е. общий член ряда стремится к нулю, но как мы видели выше, этот ряд расходится.
Необходимое условие можно сформулировать и как достаточный признак расходимости.
Теорема (достаточный признак расходимости). Если последовательность 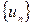 не является бесконечно малой, то ряд (1) расходится.
не является бесконечно малой, то ряд (1) расходится.
Таким образом, доказанная теорема иногда позволяет, не вычисляя частичной суммы Sn, сделать заключение о расходимости того или иного ряда. Например, ряды 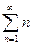 ,
, 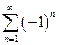 ,
, 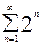 и
и 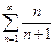 расходятся, так как соответствующие последовательности
расходятся, так как соответствующие последовательности 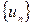 не является бесконечно малыми:
не является бесконечно малыми:
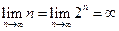 ,
, 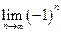 не существует,
не существует, 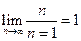 .
.
Дата добавления: 2020-05-20; просмотров: 682;











