Температура и вакуум
Температурой абсолютного вакуума считают Т = 0 К. В настоящее время достигнуты температуры 2,65·10-3…
…2,5·10-4 К и возможности не исчерпаны. Но абсолютного нуля вряд ли можно достичь, так как при нем ожидается неподвижность материи.
Поскольку (см. ранее) 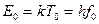 , то температура есть способ косвенного измерения частоты.
, то температура есть способ косвенного измерения частоты.
Величина 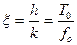 как коэффициент пропорциональности между температурой и частотой была получена М. Планком в 1900 году при анализе уравнения Вина по распределению энергии излучения черного тела. С тех пор она не использовалась: теперь ее второе рождение. Для гелия при
как коэффициент пропорциональности между температурой и частотой была получена М. Планком в 1900 году при анализе уравнения Вина по распределению энергии излучения черного тела. С тех пор она не использовалась: теперь ее второе рождение. Для гелия при 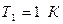 :
:
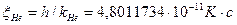 ;
;
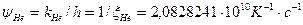 ;
;
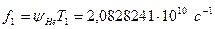 .
.
Как видно 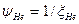 является частотной ценой одного градуса; а в непосредственной близости от
является частотной ценой одного градуса; а в непосредственной близости от  осцилляторы обладают еще колоссальной частотой колебания. При достижении
осцилляторы обладают еще колоссальной частотой колебания. При достижении 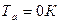 будет
будет 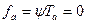 , но если принять некоторую
, но если принять некоторую 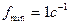 , то получим
, то получим 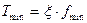 (для гелия
(для гелия 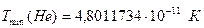 ) – это близкая к минимальной температура, при которой еще существует частотная форма движения в микромире (всего 1 Гц).
) – это близкая к минимальной температура, при которой еще существует частотная форма движения в микромире (всего 1 Гц).
Поскольку максимально зафиксированная температура (в плазме)
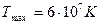 ,
,
то максимальная частота осциллятора будет
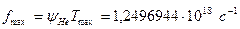 .
.
При абсолютном нуле 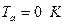 царит абсолютный покой. При других температурах может быть относительный покой. Так в нейтроне давление составляет
царит абсолютный покой. При других температурах может быть относительный покой. Так в нейтроне давление составляет 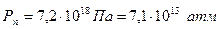 , при котором подвижность частиц электрона и электрино невозможна.
, при котором подвижность частиц электрона и электрино невозможна.
Определение температуры. Из формулы 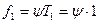 следует, что
следует, что 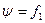 , то есть частоте осцилляторов вещества при температуре
, то есть частоте осцилляторов вещества при температуре 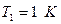 . Подставим
. Подставим 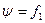 в общее уравнение
в общее уравнение 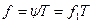 , из которого следует:
, из которого следует: 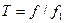 . Это и есть определение температуры: «температура есть отношение реальной частоты осцилляторов вещества к нормированной частоте (при
. Это и есть определение температуры: «температура есть отношение реальной частоты осцилляторов вещества к нормированной частоте (при 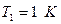 )».
)».
Умножив числитель и знаменатель на 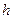 , получим другое, но аналогичное, определение температуры
, получим другое, но аналогичное, определение температуры
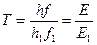 : «температура есть отношение реальной энергии осциллятора вещества к нормированной энергии (при
: «температура есть отношение реальной энергии осциллятора вещества к нормированной энергии (при 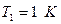 )». Хотя порознь частота
)». Хотя порознь частота 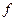 и
и 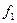 разные для разных веществ, но их отношение
разные для разных веществ, но их отношение 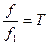 одинаково для разных веществ при одной и той же температуре, так как температурная шкала является единой для любого вещества.
одинаково для разных веществ при одной и той же температуре, так как температурная шкала является единой для любого вещества.
Мысленно представим единственную глобулу с единственным осциллятором гелия, изолированную при нормальных условиях. Тогда линейная скорость осциллятора 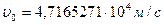 , а его амплитуда равна диаметру глобулы
, а его амплитуда равна диаметру глобулы 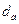 . Получим ряд важнейших термодинамических характеристик абсолютной глобулы:
. Получим ряд важнейших термодинамических характеристик абсолютной глобулы:
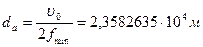 (23,6 км);
(23,6 км);
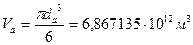 ;
;
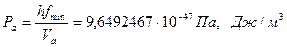 ;
;
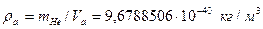 ;
;
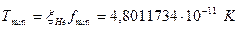 .
.
Эти данные должны быть ориентиром, в том числе, для понимания значения абсолютного вакуума, который достигается (мысленным) исключением последнего осциллятора, когда вышеперечисленные значения обращаются в нуль. Кстати космический вакуум имеет порядок 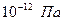 , то есть – далеко не абсолютный.
, то есть – далеко не абсолютный.
Термодинамика
В природе не существует замкнутых термодинамических систем. Термодинамические процессы непременно сопровождаются фазовыми переходами вещества, так как даже у гелия – самого инертного из газов – имеются в нормальных условиях 0,08196% молекул, которые находятся в динамическом равновесии с атомами 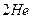
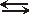
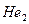 . То есть коэффициент конденсации–диссоциации
. То есть коэффициент конденсации–диссоциации 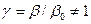 не равен единице. Именно из-за фазовых переходов не все равно каким путем система переходит из одного состояния в другое.
не равен единице. Именно из-за фазовых переходов не все равно каким путем система переходит из одного состояния в другое.
Неравновесность системы определяется градиентом частоты ее осцилляторов; система стремится к равновесию – равенству частот. Энергия распространяется только от большей частоты к меньшей. Обратный процесс возможен через третье тело, испытывающее фазовый переход.
Теплопроводность – это есть энергопроводность, когда осцилляторы с большей частотой передают ее осцилляторам с меньшей частотой путем конвективного перемешивания. Энергопередача в системе стенка – пристенный слой осуществляется только частотным механизмом.
Расчет показывает, что за период контакта глобулы осциллятора пристенного слоя со стенкой порядка ~10-7 с путь, проходимый глобулой, составляет 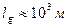 , а путь самого осциллятора
, а путь самого осциллятора 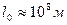 . Несмотря на то, что этот путь равен по протяженности полрасстояния до Луны, он является абсолютно беззатратным, так как в объеме глобулы осциллятор является единственным телом, движущимся в истинном вакууме. В то же время перемещение глобулы относительно соседних происходит с трением и поэтому является энергетически затратным процессом.
. Несмотря на то, что этот путь равен по протяженности полрасстояния до Луны, он является абсолютно беззатратным, так как в объеме глобулы осциллятор является единственным телом, движущимся в истинном вакууме. В то же время перемещение глобулы относительно соседних происходит с трением и поэтому является энергетически затратным процессом.
Коэффициент теплопередачи (энергопередачи) при естественной, например, конвекции у стенки пропорционален частоте осцилляторов пристенного слоя, шероховатости стенки, критическому расстоянию взаимодействия осцилляторов и обратно пропорционален объему глобул газа вдали от стенки:
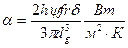 .
.
Механизм возникновения конвективного тока газа логично представить следующим образом. Пусть (мысленно) одна глобула на дне получает приращение частоты и энергии. Объем глобулы возрастает, плотность становится меньше окружающих и она всплывает, расталкивая соседей. Ее место занимает другая глобула и затем направляется вверх ровно вслед первой. Так возникает элементарный восходящий ток конвекции. Всплывающую глобулу тормозит взаимодействие с соседями по всему периметру глобулы  .
.
Это торможение пропорционально частоте 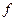 осциллятора, то есть количеству взаимодействий с соседями в единицу времени, его массе
осциллятора, то есть количеству взаимодействий с соседями в единицу времени, его массе 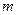 и коэффициенту
и коэффициенту 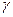 :
:
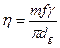 –
–
такая совокупность тормозящих факторов есть вязкость газа.
Диффузия происходит в сплошной среде и без градиента концентрации, как это ныне принято. Диффузия обусловлена блужданием глобулы. В равновесной системе, где нет никаких градиентов полей, скорость блуждания обусловливает диффузию – беспрерывное перемешивание осцилляторов. В этом случае все шесть ( 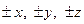 ) направлений равновероятны и средняя скорость диффундирования молекулы составляет одну шестую скорости блуждания
) направлений равновероятны и средняя скорость диффундирования молекулы составляет одну шестую скорости блуждания 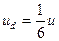 .
.
Теплоемкость, в частности изобарная, является суммой следующих энергетических статей расхода: на конденсацию – диссоциацию, на изменение частоты осцилляторов, на заполнение пространства, на перемещение глобул. Эти статьи, например, для кислорода, находятся в отношении ( 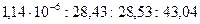 )
)  . Несмотря на малый процент энергозатрат на конденсацию – диссоциацию, само наличие малой доли более мелкой фазы способствует возникновению начала различных, в том числе, химических реакций, так как реакции на мелких фазах легче преодолевают активационный энергетический барьер.
. Несмотря на малый процент энергозатрат на конденсацию – диссоциацию, само наличие малой доли более мелкой фазы способствует возникновению начала различных, в том числе, химических реакций, так как реакции на мелких фазах легче преодолевают активационный энергетический барьер.
6. Механизм электродинамического
взаимодействия осцилляторов
Энергия единичного 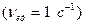 взаимодействия осциллятора имеет следующие выражения:
взаимодействия осциллятора имеет следующие выражения:
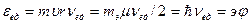 .
.
Элементарный электрический потенциал
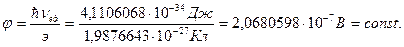
(постоянная Чедвика).
Для элементарного осциллятора-нейтрона
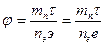 (
( 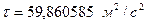 – постоянная Томсона).
– постоянная Томсона).
Поскольку знак 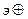 , а
, а 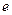 –, то
–, то 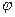 – меняет знак при взаимодействии осцилляторов – то есть имеет место двукратное взаимодействие электрино с осциллятором в одном акте.
– меняет знак при взаимодействии осцилляторов – то есть имеет место двукратное взаимодействие электрино с осциллятором в одном акте.
Из формулы (постоянная Перрена)
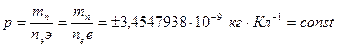
следует, что любой атом, любая молекула, любое композиционное тело в природе непременно обладает одновременно положительными и отрицательными электрическими полями. Кроме того, как видно, нет массы без заряда и нет заряда без массы.
Потенциал осциллятора 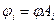 связан с элементарным потенциалом через атомное число, так как пропорционален количеству нейтронов.
связан с элементарным потенциалом через атомное число, так как пропорционален количеству нейтронов.
Физическая суть постоянной Томсона 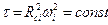 , где
, где 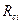 – радиус вращения осциллятора, делящий его массу пополам;
– радиус вращения осциллятора, делящий его массу пополам; 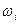 – угловая скорость вращения. Отсюда следует, что линейная скорость вращения центра массы всех тел постоянна:
– угловая скорость вращения. Отсюда следует, что линейная скорость вращения центра массы всех тел постоянна:
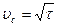
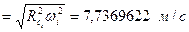 .
.
Этот закон проверен на вращении микротел (атомы, молекулы) и макротел (планеты).
Расчет показывает, что электроны в нейтроне утоплены в массе электрино на 97,546 % и лишь узкими глазками обращены наружу. Радиус вращения и угловая скорость осциллятора – нейтрона:
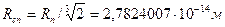 ;
;
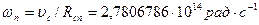 .
.
Положительное электрическое поле распространяется в пространство сферически – это фоновое поле, так как оно занимает 99,99934% поверхности нейтрона. На фоне изотропного по поверхности положительного поля, отрицательное поле трех глазков электронов беспрерывно вращается, изменяя направление вращения при каждом акте взаимодействия. Положительное поле обеспечивает постоянное отталкивание осцилляторов, полярные поля развивают взаимное притяжение.
Алгоритм взаимодействия двух осцилляторов следующий. После сближения на критическое расстояние электронный луч осциллятора – 1 отрывает электрино от осциллятора – 2. Это электрино внешнего слоя мгновенно набирает скорость
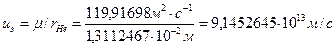 (для
(для 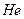 ).
).
Электрино развивает импульс 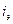 . Пока электрино не вышло из поля электрона, оба осциллятора продолжают сближение, вращаясь. В результате вращения электрино выходит из поля электронного луча и вступает во взаимодействие с положительным полем осциллятора – 1: то есть после притяжения отталкивается. При этом осциллятор – 1 получает половину импульса электрино и останавливается:
. Пока электрино не вышло из поля электрона, оба осциллятора продолжают сближение, вращаясь. В результате вращения электрино выходит из поля электронного луча и вступает во взаимодействие с положительным полем осциллятора – 1: то есть после притяжения отталкивается. При этом осциллятор – 1 получает половину импульса электрино и останавливается: 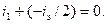
В результате изменения направления движения на противоположное электрино вгоняется назад в собственный локус (локальное гнездо, образованное шестью окружающими электрино внешнего слоя). Передача второй половины импульса 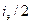 собственному осциллятору – 2 приводит к остановке его поступательного движения. При этом оба осциллятора продолжают свое вращение, поступательного движения нет.
собственному осциллятору – 2 приводит к остановке его поступательного движения. При этом оба осциллятора продолжают свое вращение, поступательного движения нет.
Далее осцилляторы меняются ролями и акт взаимодействия повторяется симметрично. В результате осциллятор – 2 получает номинальный импульс, претерпевает ротацию на 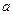 рад и покидает точку стояния. Электрино же при передаче импульса осциллятору – 2 меняет направление и вгоняется в свой локус в осцилляторе – 1. Осциллятор – 1 получает номинальный импульс, претерпевает ротацию на
рад и покидает точку стояния. Электрино же при передаче импульса осциллятору – 2 меняет направление и вгоняется в свой локус в осцилляторе – 1. Осциллятор – 1 получает номинальный импульс, претерпевает ротацию на 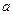 рад и покидает точку взаимодействия с осциллятором – 2. На этом акт взаимодействия заканчивается.
рад и покидает точку взаимодействия с осциллятором – 2. На этом акт взаимодействия заканчивается.
Следует отметить, что электронный луч (так же, как и электринный) – это зарядовый луч электрического поля, который лишен свойства расходиться и распространяется в пространстве с бесконечной скоростью. Вследствие равновесия сил электрино, вырванное из нейтрона, висит над своим локусом на расстоянии 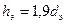 для гелия,
для гелия, 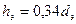 для ксенона. При этом электростатическая сила равна
для ксенона. При этом электростатическая сила равна 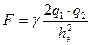 , где
, где 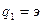 – заряд электрино;
– заряд электрино; 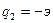 – заряд поставляемый электронами;
– заряд поставляемый электронами; 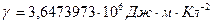 – постоянная электростатического взаимодействия зарядов. Эта сила противодействует отрыву электрино электронным лучом; электрино находится над локусом
– постоянная электростатического взаимодействия зарядов. Эта сила противодействует отрыву электрино электронным лучом; электрино находится над локусом 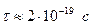 (для
(для 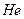 ).
).
Эта же формула 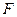 объясняет гравитацию как перекрестное замыкание полей композиционных тел.
объясняет гравитацию как перекрестное замыкание полей композиционных тел.
Дата добавления: 2016-06-29; просмотров: 4690;











