Нелинейная модель биполярного транзистора

При изучении транзисторов с учетом их инерционных свойств недостаточно использовать статические характеристики. Связь между токами и напряжениями в этом случае определяется системой нелинейных дифференциальных уравнений.

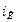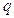Процессы в биполярных транзисторах в значительной части диапазона рабочих частот удовлетворительно описываются нелинейной зарядовой моделью [1] (рис.1.13), определяющей связь токов коллектора и базы с избыточным зарядом неосновных носителей в базе и зарядом барьерных емкостей эмиттерного и коллекторного переходов. Емкость принято разделять на две составляющие

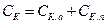, (1.1)

где - емкость активной части, расположенной непосредственно под эмиттером, 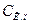- емкость оставшейся, пассивной части перехода.

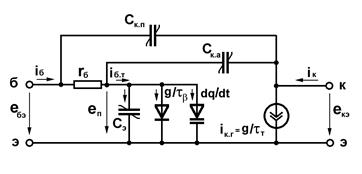
Рисунок 1.13 – Нелинейная зарядовая модель биполярного транзистора

Исходя из рис.1.13, запишем выражения для части токов ( , 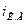) биполярного транзистора

, (1.2)

Здесь - ток коллекторного генератора тока, управляемого избыточным зарядом в базе; - ток базы теоретической модели; - среднее время пролета носителей через базу; - среднее время жизни неосновных носителей в базе.

Величину можно оценить по приводимой в справочниках граничной частоте 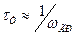, a . Последнее соотношение вытекает непосредственно из (1.2), поскольку статический коэффициент передачи тока базы

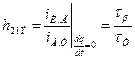. (1.3)

При использовании метода заряда считается, что накопленный в базе заряд связан с напряжением на эмиттерном переходе безынерционной зависимостью

, (1.4)

где 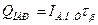- обратный тепловой ток базы; - температурный потенциал (при ).

Из (1.2) видно, что составляющая тока коллектора 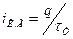также безынерционно связана с зарядом q, а, следовательно, и с напряжением на переходе. Фактически ток определяется градиентом заряда 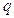у коллекторного перехода, изменение которого запаздывает на время порядка долей относительно изменения интегрального заряда 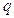. Пренебрежение этим запаздыванием определяет область частот 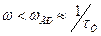, где рассматриваемая модель применима.

Согласно зарядовой модели (см. рис.1.13) полные выражения для токов имеют вид

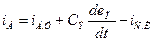, (1.5)

где токи и определяются по (7.2), a ток смещения через суммарную емкость :

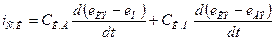(1.6)

Дополним (1.2) - (1.6) дифференциальным уравнением для напряжения на переходе. Для этого в соответствии со схемой рис.1.13 запишем составляющую тока базы, протекающую через эмиттерный переход,

как сумму токов через сопротивление базы и емкость :

.

Подставив сюда из (1.2), получим

(1.7)

Система уравнений (1.2) - (1.7) определяет процессы в транзисторе, работающем в активной области и области отсечки. Для инженерных расчетов усилителей мощности и умножителей частоты малой кратности нелинейную зависимость (1.4) в области рабочих значений накопленного заряда можно заменить кусочно-линейной:

, (1.8)

где - средняя для рабочей части активной области диффузионная емкость; 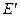-напряжение отсечки (индекс 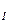здесь и далее показывает, что транзистор открыт).

Подставив (1.8) в (1.2), получим аппроксимированные характеристики токов теоретической модели

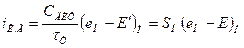, (1.9)

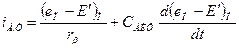, (1.10)

где 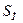, - усредненные крутизны коллекторного и базового токов по напряжению на переходе, причем

, .

Дифференциальные параметры зарядовой модели

, ,

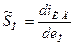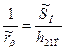
при линейно зависят от тока коллектора:

, ,

Поэтому для повышения точности расчетов при применении кусочно-линейной аппроксимации характеристик транзистора (1.8) - (1.10) необходимо учитывать рабочую высоту импульса коллекторного тока . Рекомендуется брать усредненные параметры 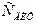, , 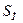равными их дифференциальным значениям при токе и проводить аппроксимирующую прямую через точку, соответствующую току .

В статическом режиме ток коллектора 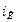равен току гене­ратора 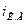, а напряжение 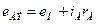. Пример аппроксимации статических характеристик и показан на рис.1.14.

Аппроксимированные характеристики определяются соотношениями

, (1.11)

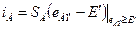, (1.12)

где ; ; - средний для активной области коэффициент деления напряжения во входной цепи транзистора на низких частотах

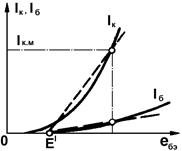
Рисунок 1.14 - Статические характеристики, соответствующие зарядовой модели, и их аппроксимация

(1.13)

Принятой полигональной аппроксимации соответствует кусочно-линейная высокочастотная модель биполярного транзистора (рис.1.15).

Для упрощения анализа нелинейные емкости , и здесь также заменены постоянными, равными средним для рабочих интервалов напряжений значениям. При замкнутом положении ключа ( ) транзистор находится в активной области, а при разомкнутом - в области отсечки. Переход из одной области в другую происходит в тот момент, когда напряжение на переходе 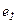проходит через напряжение отсечки .

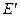Рисунок 1.15 – Кусочно-линейная высокочастотная модель

биполярного транзистора для областей активной и отсечки