Магнитное поле и его характеристики

Физические основы магнитного неразрушающего контроля

Магнитный вид неразрушающего контроля основан на анализе взаимодействия магнитного поля и объекта контроля (ОК). Он применим лишь к деталям из металлов и сплавов, способных к намагничиванию. Основные задачи магнитного неразрушающего контроля (НК): контроль сплошности – дефектоскопия, измерение размеров – толщинометрия, контроль физико-механических свойств – структуроскопия. В отличие от двух последних на железнодорожном транспорте актуальна магнитная дефектоскопия, с помощью которой выявляют поверхностные и подповерхностные дефекты на свободных или открытых для доступа частях деталей.

На железнодорожном транспорте магнитному контролю подвергают следующие объекты подвижного состава: детали ударно-тягового и тормозного оборудования, рамы тележек различных моделей в сборе и по элементам, оси колесных пар вагонов и локомотивов всех типов в сборе, ободы, гребни и спицы локомотивных колес, свободные кольца буксовых подшипников, а также внутренние кольца, напрессованные на шейки оси, венцы зубчатых колес и шестерен тягового редуктора, валы генераторов, тяговых двигателей и шестерен в сборе, упорные кольца, стопорные планки, пружины, шкворни, болты и т.д. такая широкая номенклатура контролируемых объектов предполагает достаточно большое разнообразие методов, средств и технологических приемов магнитного контроля. При этом физическая сущность магнитной дефектоскопии для всех объектов является единой.

Методической основой технологии магнитного контроля являются государственные стандарты [1–3], руководящие документы [4–7].

Магнитное поле и его характеристики

Общеизвестно, что в «пустом» пространстве существует силовое поле, если на предмет, находящийся в этом пространстве, действует сила. Например, человек постоянно испытывает действие гравитационного поля: где бы он ни находился, Земля притягивает его с силой

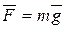, (1.1)

где m – масса тела; 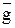– ускорение свободного падения (характеристика самого поля).

Для всех физических полей структура формулы для определения силы поля одинакова [8, 9]. В ней всегда фигурирует произведение одной или нескольких величин, характеризующих тело (масса, заряд, скорость и т. д.), умноженное на векторную величину, которая характеризует поле в точке его местоположения. Эта величина называется напряженностью поля. В выражении (1) ускорение свободного падения 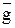есть напряженность гравитационного поля.

Каждое силовое поле создается теми и только теми телами, на которые оно может действовать. Например, любой предмет, независимо от размера, массы, цвета и т.д., создает вокруг себя гравитационное поле, которое притягивает к себе другие предметы вдоль линии, соединяющей их центры тяжести.

Возьмем другое по физической природе поле – электростатическое (кулоновское). Оно действует только на заряженные тела с силой

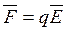, (1.2)

где q – электрический заряд тела; 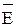– напряженность электростатического поля в месте его нахождения.

Подчеркнем, что электростатическое поле более избирательно, оно создается только заряженными телами, заряды q которых могут быть и положительными, и отрицательными, тогда как масса m всегда положительна, несмотря на то, что формулы одни и те же: чтобы определить силу, надо определенную величину, относящуюся к телу, умножить на напряженность поля в этой точке.

Рассмотрим физические поля (рис. 1.1), которые представляют силовые линии. Главное свойство такой линии поля состоит в том, что в любой точке, через которую она проходит, направление вектора напряженности совпадает с направлением касательной к ней в этой же точке (рис. 1.1, а). Длины векторов, т. е. значения напряженности во всех точках силовой линии, одинаковы. Проведенная на рисунке одна силовая линия задает направление напряженности в бесконечном числе лежащих на ней точек. Если поле сильнее, то, следовательно, величина напряженности больше там, где линии будут расположены гуще, и слабее – где они разряжены (рис. 1.1, б). В то же время силовые линии не могут пересекать друг друга.

а 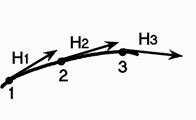б

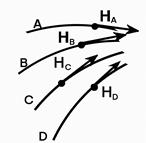
Рис. 1.1. напряженность на силовой линии
и в точках магнитного поля

Таким образом, по совокупности линий можно судить не только о направлении, но и о значениях напряженности магнитного поля. Поле, напряженность которого одинакова во всех точках, называется однородным. В противном случае оно неоднородно.

Магнитное поле – это один из видов силовых полей, но в отличие от электро-статического оно еще более избирательно – действует только на движущиеся заряды. На неподвижные заряженные предметы, даже в самых сильных магнитных полях, не действует никакая сила. Становится очевидным, что «конструкция» формулы для определения силы, действующей на движущееся тело в магнитном поле, должна быть сложнее предыдущих [8, 9].

Действительно, для гравитационного поля важна лишь масса тела m, для кулоновского – величина его заряда q, а для магнитного поля важными оказываются сразу три фактора: заряд тела, численное значение скорости его движения и направление скорости. Сила, приложенная к движущемуся заряженному телу со стороны магнитного поля, называется силой Лоренца:

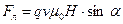, (1.3)

где q – электрический заряд тела; v – скорость заряженного тела; a – угол между направлениями векторов скорости 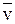и напряженности магнитного поля 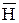в точке, где находится тело; μ₀ – размерный коэффициент.

Напряженность магнитного поля Н – его силовая характеристика, не зависящая от магнитных свойств среды, в которой поле существует. Она характеризует магнитное поле по величине и направлению, но учитывает только влияние на интенсивность поля проводников с токами и расположение магнитов. В системе СИ измеряется в амперах на метр – А/м или А·м^-1. Для того чтобы описать вектор напряженности магнитного поля 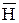, поместим его в прямоугольную систему координат на поверхности детали, соединив начала вектора и системы координат, и найдем его составляющие 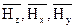(рис. 1.2) [8]. Такое представление удобно в работе, так как проще измерять не вектор в целом, а его компоненты. Особенно часто используют компоненты 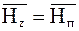(векторы) – нормальная составляющая, как правило, перпендикулярная поверхности детали, и 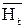– тангенциальная составляющая с модулем 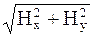, направленная параллельно поверхности.

Заменим произведение нескольких параметров, характеризующих тело в уравнении (1.1), на единственный, более сложный, чем масса или заряд, параметр, который называется магнитным моментом.

Куда направлена сила магнитного поля? В гравитационном поле сила всегда направлена в ту же сторону, что и ускорение свободного падения, так как тел с отрицательной массой не бывает. При положительном заряде в кулоновском поле сила F и напряженность Е всегда направлены вдоль прямой, соединяющей два заряда, причем в одну сторону, и в разные – при отрицательном заряде тела.

В магнитном поле сила Лоренца F_л всегда перпендикулярна и к напряженности вектора 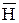, и к скорости тела 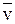. Очевидно, что единственная прямая, перпендикулярная одновременно вектору 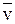и 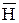– есть перпендикуляр к плоскости, в которой лежат эти векторы (рис. 1.3, а) [10].

а 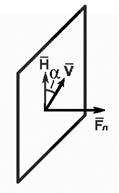б

Рис. 1.3. Силы Лоренца (а) и Ампера (б)

Если изменить на противоположное направление скорости 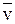или напряженности 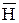, то поменяется на противоположное и направление силы F_л. Последнее можно определять по известному правилу левой руки.

В случае, при котором носителями зарядов является движущийся в проводнике поток электронов, силы Лоренца, приложенные к каждому электрону в потоке, суммируясь, прижимают их к стенке провода, толкая его поперек движения электронов, т. е. перпендикулярно направлению электрического тока. В результате формула (1.1) преобразуется и значение силы, действующей на проводник длиной l с током I, расположенный под углом α к направлению поля Н (рис. 1.3, б), будет определяться законом Ампера:

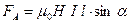. (1.4)

Если ток течет в контуре в виде плоской рамки в однородном поле Н, направленном параллельно сторонам АВ и СД (рис. 1.4, а), то возникают две силы Ампера, воздействующие перпендикулярно сторонам ВС и ДА
(a = 90°), параллельные между собой и направленные противоположно, которые образуют на плече b/2 пару сил с моментом

, (1.5)

где 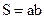– площадь рамки.

Формулу (1.5) можно представить в виде:

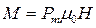, (1.6)

где величину 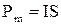называют магнитным моментом контура. Единицей измерения 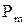является А·м² – «амперквадратный метр».

Если рассматривать плоский контур произвольной формы с током в однородном магнитном поле, то необходимо просуммировать воздействие Н на отдельные малые элементы контура, то результат останется тем же: формула (1.6) будет справедливой. Магнитному моменту 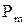контура придают векторный характер. Условимся за направление 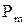принимать направление положительной нормали к контуру с током по правилу правозаходного винта (рис. 1.4) [10].

а 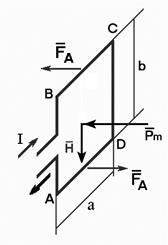б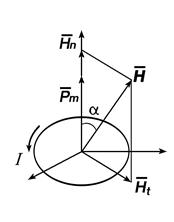

Рис. 1.4. Магнитный момент: а – рамки с током;
б – произвольного контура с током в магнитном поле

В общем случае, когда контур с током I и однородное магнитное поле Н не лежат в одной плоскости, а находятся под углом α, который на рис. 1.4, б показан, как угол между направлением поля Н и нормали ( 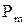) к контуру, то магнитное поле Н можно разложить на две составляющие: 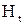и 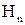. Тогда тангенциальная составляющая ( 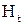) будет лежать в плоскости контура, а нормальная ( 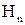) – перпендикулярна ему. При этом 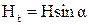и 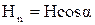. Вращающий момент создает только составляющая 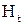, т. е.

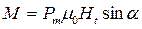(1.7)

или в векторной форме:

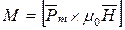. (1.8)

Для более компактного по сравнению с выражением (1.8) описания силового воздействия магнитного поля введем в рассмотрение понятие магнитной индукции В, которая, как и напряженность Н, является величиной векторной и служит основной характеристикой магнитного поля. Величины В и Н связаны соотношением:

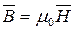. (1.9)

Здесь размерный коэффициент μ₀ в системе СИ равен 4π10^-7 Гн/м. Его называют также магнитной постоянной или магнитной проницаемостью вакуума, придавая этим данному коэффициенту определенный физический смысл. Тогда с учетом уравнения (1.9) выражение (1.8) можно представить в виде векторного произведения:

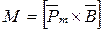, (1.10)

т. е. формула для определения силового воздействия на контур с током в магнитном поле становится такой же простой, как в гравитационном и электростатическом. Основное различие заключается в том, что для двух последних формулы (1.1) и (1.2) определяют силы, действующие на пробное тело, а формула (1.10) определяет момент сил. Под действием гравитационного и электростатического поля пробное тело движется поступательно. Контур с током под действием однородного магнитного поля испытывает поворот. Под действием неоднородного поля контур одновременно и вращается, и поступательно перемещается.