Истечение через насадки
Насадком называется короткая трубка длиной от двух до шести диаметров, присоединённая к выходу отверстия, через которое истекает жидкость. Роль насадка может выполнять и отверстие в толстой стенке, когда диаметр отверстия значительно меньше её толщины. Насадки отличаются формой и размерами. Наиболее существенные отличия между насадками состоят в форме входного отверстия, которая, как уже отмечалось выше, может существенно влиять на величину расхода при той же самой площади проходного сечения.
 Рисунок 3.30 – Истечение жидкости через насадки
Рисунок 3.30 – Истечение жидкости через насадки
Простейшим насадком является цилиндрический насадок (рисунок 3.30). Течение в нём может происходить в двух разных режимах. В первом случае на острых входных кромках насадка происходит совершенное сжатие струи и далее она движется, не касаясь стенок насадка. В этом случае истечение ничем не отличается от истечения через малое отверстие в тонкой стенке. Скорость при этом истечении высокая, а расход минимален.
Во втором случае, как и при истечении через отверстие в тонкой стенке, струя жидкости вначале сжимается на некотором удалении от входного сечения, образуя вихревую зону, давление в этом сечении струи становится меньше атмосферного. Далее струя постепенно расширяется и заполняет всё сечение насадка. Из-за того, что сжатия на выходе насадка нет (ε = 1,0) а коэффициент расхода через такой насадок равняется 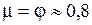 .
.
При этом расход жидкости через насадок при прочих равных условиях превышает расход в первом случае, а скорость жидкости становится меньше из-за более высокого сопротивления.


а) б)
Рисунок 3.31 – Истечение жидкости через насадки
Ещё лучшие условия истечения наблюдаются при движении жидкости через так называемый тороидальный насадок (рисунок 3.31, а), который обеспечивает более высокий коэффициент расхода. Его значение, в зависимости от увеличения радиуса скругления кромки, доходит до 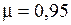 .
.
Когда радиус кривизны становится больше длины насадка, насадок становится коноидальным (рисунок 3.31, б). Коэффициент расхода в таких условиях истечения приближается к значению 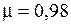 .
.
3.15Гидравлический расчет трубопроводов
3.15.1 Виды трубопроводов
Устройства, предназначенные для подвода рабочей жидкости от одного элемента к другому при работе гидропривода называют гидравлической линией. По назначению гидролинии делятся на:
ü всасывающие – для подвода жидкости к насосам;
ü напорные – для подачи жидкости к распределителям и гидродвигателям;
ü сливные – для отвода жидкости в резервуары;
ü дренажные – для отвода утечек от гидромашин и гидроаппаратов;
ü линии управления – для подвода жидкости к элементам гидропривода.
Существующие водопроводные, нефтепроводные, газовые сети делят на два типа:
ü магистральные трубопроводы, подающие ту или иную среду от источника к потребителю на большие расстояния;
ü разветвлённые сети труб, обеспечивающие распределение этой среды непосредственно потребителям.
С конструктивной точки зрения трубопроводы подразделяют на:
ü простые;
ü сложные;
ü короткие;
ü длинные.
Простыминазывают трубопроводы, не имеющие ответвлений и обслуживающие только одну точку Þ x. Причем, диаметр трубы, а также расход жидкости на всей длине трубы остается неизменным.
Сложные трубопроводы делятся на тупиковые, параллельные и кольцевые.
Тупиковыесостоят из магистрального (главного) трубопровода, от которого в разные стороны отходят ответвления к потребителям.
Параллельныесостоят из нескольких параллельно проложенных трубопроводов, связанных между собой перемычками с регулирующими задвижками.
Кольцевыепредставляют собой замкнутую сеть труб, что обеспечивает подачу воды в любом направлении. При аварии на каком-либо участке подача воды потребителю не прекращается.
Трубопроводы, у которых местные потери напора составляют менее 10 % от потерь по длине, считаются гидравлически длинными, если же более 10 %, то гидравлически короткими.
Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад может быть создан:
ü работой насоса;
ü благодаря разности уровней жидкости;
ü давлением газа.
В основном приходится иметь дело с такими трубопроводами, движение жидкости в которых обусловлено работой насоса.
3.15.2 Расчет простого трубопровода
Одна из задач расчёта трубопровода – определить минимальную мощность, необходимую для доставки данного количества жидкости в заданную точку, т.е. на определённое расстояние.
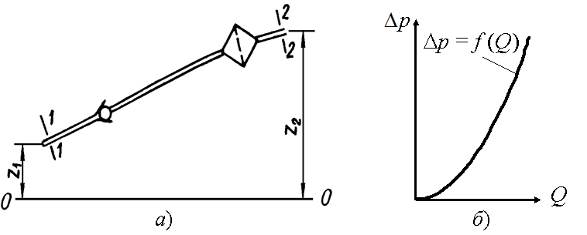
Рисунок 3.32 - Простой трубопровод (а) и характеристика простого
трубопровода(б)
Пусть простой трубопровод (рисунок 3.32, а) постоянного сечения расположен произвольно в пространстве, имеет общую длину l и диаметр d и содержит ряд местных сопротивлений. В начальном сечении (1-1) имеем нивелирную высоту z1 и избыточное давление р1, а в конечном (2-2) – соответственно z2и р2. Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна  .
.
Запишем уравнение Бернулли сечений 1-1 и 2-2
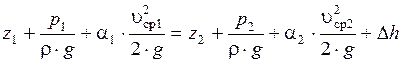 ;
;
где 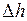 – сумма потерь полного напора на участке между сечениями;
– сумма потерь полного напора на участке между сечениями;
υср – средняя величина скорость по сечению;
a– коэффициент Кориолиса, учитывающий неравномерность распределения скорость по сечению потока.
Суммарные потери на трение по длине и на местных сопротивлениях на участке трубы длиной l. Потери будут определяться по формулам
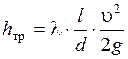 и
и 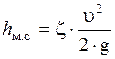 .
.
Учитывая уравнение неразрывности потока и постоянство диаметра трубы т. е. 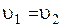 и
и 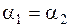 , скоростные напоры в обеих частях можно сократить. Тогда уравнение Бернулли примет вид
, скоростные напоры в обеих частях можно сократить. Тогда уравнение Бернулли примет вид
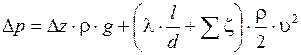 (1)
(1)
Выразив величину скорости через расход и подставив в выражение (1) получим формулу
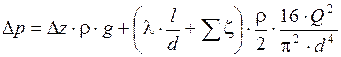
или 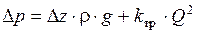 (2)
(2)
где 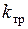 - гидравлическое сопротивление трубопровода.
- гидравлическое сопротивление трубопровода.
Выражение (2) называется характеристикой трубопровода при турбулентном движении жидкости. Эта характеристика представляет собой зависимость суммарных потерь давления (напора) от расхода в трубопроводе 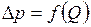 (
( 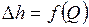 ) (рисунок 3.32, б).
) (рисунок 3.32, б).
Если в трубопроводе установлены гидравлические аппараты, имеющие свои сопротивления, то их необходимо добавить к коэффициенту сопротивления трубопровода, и в результате получится суммарное гидравлическое сопротивления.
Дата добавления: 2016-06-22; просмотров: 2889;











