Переменный ток в конденсаторе
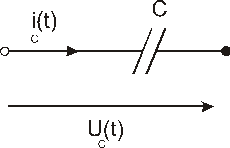
Конденсатор представляет собой две металлические пластины, разделенные диэлектриком, поэтому постоянный ток (или постоянная составляющая тока) через конденсатор не течет!
На обкладках конденсатора накапливается заряд, пропорциональный напряжению на конденсаторе. Коэффициентом пропорциональности выступает ёмкость конденсатора, обозначаемая буквой С [ф]. 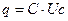 . Размерность ёмкости – фарада. Это очень большая величина, поэтому используются её производные
. Размерность ёмкости – фарада. Это очень большая величина, поэтому используются её производные 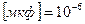 ;
; 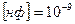 ;
;  .
.
Если напряжение на обкладках конденсатора будет меняться, то и заряд тоже будет меняться:
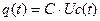
Изменение заряда создает в цепи конденсатора ток:
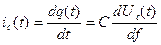 (1)
(1)
Таким образом, ток, протекающий через конденсатор, равен производной от напряжения по времени, умноженной на ёмкость С.
Из уравнения (1) определим напряжение на конденсаторе:
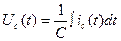 (2)
(2)
Пусть на конденсатор подаётся переменное синусоидальное напряжение 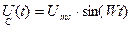 . Определим ток конденсатора по формуле (1):
. Определим ток конденсатора по формуле (1):
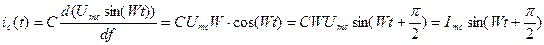
Из этого выражения видно, что на конденсаторе синусоидальный ток 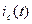 опережает по фазе напряжение
опережает по фазе напряжение 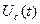 на угол
на угол 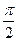 (или 90°).
(или 90°).
Амплитуда тока связана с амплитудой напряжения следующим соотношением:
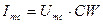 или
или 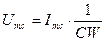
Это соотношение очень напоминает закон Ома.
Поэтому введём понятие ёмкостного реактивного сопротивления:
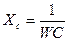 , тогда
, тогда  (3)
(3)
Если поделить левую и правую часть уравнения (3) на 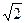 , то получим:
, то получим:
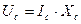 , где
, где 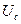 и
и 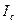 – действующие значения напряжения и тока конденсатора. Конденсатор способен накапливать энергию:
– действующие значения напряжения и тока конденсатора. Конденсатор способен накапливать энергию:
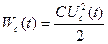 (это энергия электрического поля в конденсаторе)
(это энергия электрического поля в конденсаторе)
Производная от  – есть мгновенная мощность:
– есть мгновенная мощность:
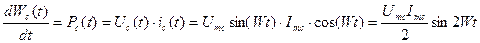
Подсчитаем значение средней за период мощности (активной мощности):
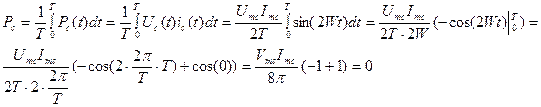
Графики 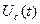 ,
, 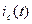 ,
, 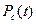 показаны на рис. 1.
показаны на рис. 1.
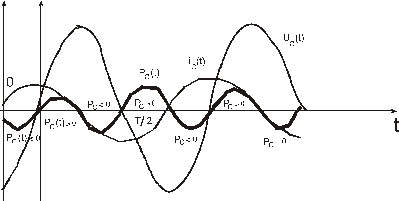
Как видно из графика, мгновенная мощность на конденсаторе изменяется синусоидально с удвоенной частотой.
Четверть периода конденсатор запасает энергию 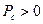 , а следующую четверть периода – отдает обратно в цепь
, а следующую четверть периода – отдает обратно в цепь 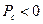 , поэтому активная мощность конденсатора (идеального, без потерь) равна нулю.
, поэтому активная мощность конденсатора (идеального, без потерь) равна нулю.
Произведение 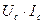 дает величину реактивной мощности конденсатора, обозначаемой
дает величину реактивной мощности конденсатора, обозначаемой 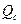 . Эта величина определяет среднее значение мощности, запасаемой в конденсаторе энергии.
. Эта величина определяет среднее значение мощности, запасаемой в конденсаторе энергии.
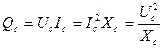
Поскольку эта мощность не совершает полезной работы, её называют реактивной, и сопротивление 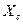 – тоже называют реактивным.
– тоже называют реактивным.
Как правило, за начальную фазу принимают фазу тока, поэтому первые четверть периода мгновенная мощность отрицательна. Реактивная мощность конденсатора при расчетах берется со знаком «–», она отрицательна.
В электротехнике часто синусоидальные токи и напряжения представлены в виде векторов, длина которых равна амплитуде или действующему значению, а угол поворота соответствует фазе. Такой вектор будет вращаться с частотой 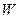 , чтобы его остановить полагают
, чтобы его остановить полагают 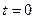 , тогда угол поворота будет равен начальной фазе g, для конденсатора
, тогда угол поворота будет равен начальной фазе g, для конденсатора  ;
; 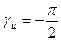

Дата добавления: 2016-05-28; просмотров: 3600;











