Метод узловых потенциалов.

В этом методе неизвестными величинами являются потенциалы узлов схемы. Поскольку один из узлов схемы может быть заземлен, т.е. его потенциал приравнивается нулю, то число неизвестных совпадает с числом независимых узлов уравнений.

Этот метод базируется на первом законе Кирхгофа, в котором токи выражены по обобщенному закону Ома.

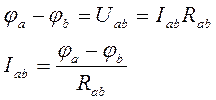
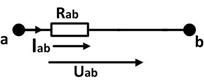- закон Ома.

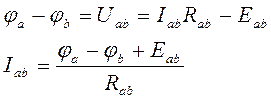
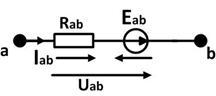
- обобщенный закон Ома.

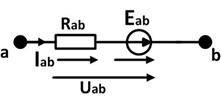При смене полярности ЭДС

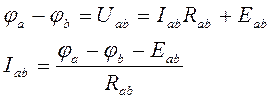уравнение выглядит так:

Если 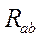выразить через проводимость 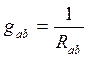, то обобщенный закон Ома будет выглядеть так:

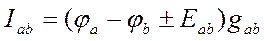
Выразим все токи в электрической цепи по обобщенному закону Ома и подставим их в систему узловых уравнений. Теперь вместо неизвестных токов в этой системе будет стоять неизвестные потенциалы узлов и заданные по условию задачи ЭДС, источники тока и проводимости ветвей.

Рассмотрим это на примере конкретной схемы:

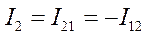
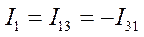
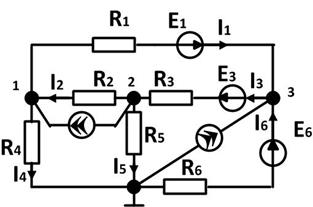
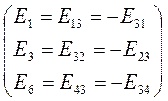
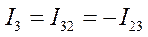
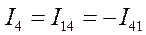
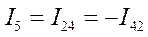
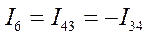
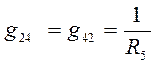
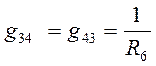
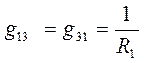
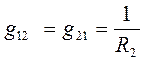
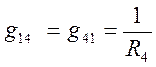
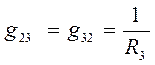
В связи с тем , что мы используем двоичные индексы, то перестановка индексов перед током и перед ЭДС меняет их знак. Перестановка индексов у проводимости ее знака не меняет.

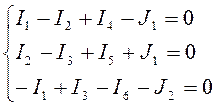
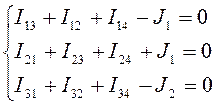
Теперь выразим токи, по обобщенному закону Ома:

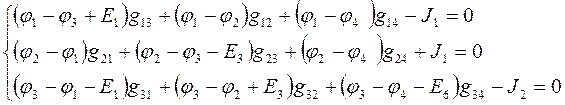
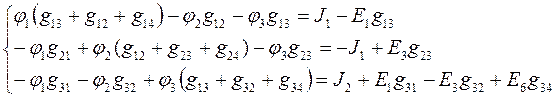
В первом уравнении после 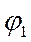стоит сумма проводимостей всех ветвей, сходящихся в первом узле. Обозначим ее 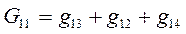. Аналогично, для второго и третьего уравнения введем суммарную проводимость второго и третьего узлов:

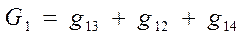
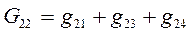
Введем проводимость 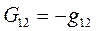, которая равна проводимости (или сумме проводимостей) всех ветвей, соединяющих первый узел 1 со вторым узлом 2, взятой со знаком минус.

Введем по аналогии взаимную проводимость 1 и 3, 2 и 3 узлов:

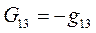и .

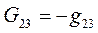Правые части уравнений нашей системы назовем узловыми токами:

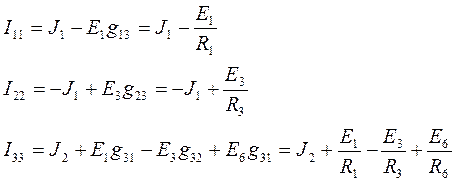
Узловой ток – это величина, равная алгебраической сумме токов, полученных от деления ЭДС ветвей, подходящих к данному узлу, на сопротивления этих ветвей. Со знаком “+” берутся токи тех ветвей, ЭДС которых направлены к узлу.

Теперь можно записать систему уравнений в общем виде для n – независимых узлов (n+1 – последний узел).

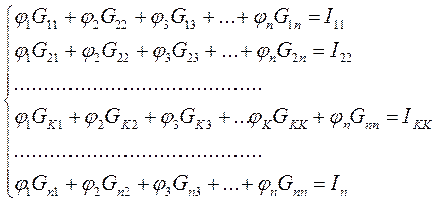
Где 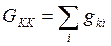- сумма проводимостей ветвей – i, сходящихся в узле K(суммарная проводимость K-го узла).

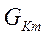- сумма проводимостей ветвей, соединяющих узлы К и m, взятая со знаком “-”(взаимная проводимость узлов К и m)

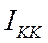- узловой ток К-го узла. Если к К-му узлу подтекает ток от источника тока, то он должен быть включен в ток 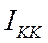со знаком “+”, если утекает,то “-”.