Метод контурных токов.

Составляя уравнения ко второму закону Кирхгофа, но удовлетворяя первому можно снизить число уравнений и получить при этом решение.

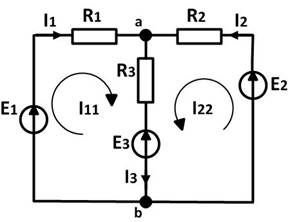
В соответствии с принципом наложения, ток в любой ветви можно представить суммой токов. Поэтому будем считать, что если ветвь входит только в один контур (внешняя ветвь), то по ней протекает ток, который мы назовем контурным и он постоянен по всему контуру. Если же ветвь входит в несколько контуров (взаимная ветвь), то через неё протекает несколько контурных токов, а общий ток равен их алгебраической сумме.

Итак, в нашем примере , .

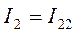По - первому закону Кирхгофа для узла “а” получим:

(*)

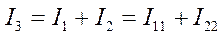Теперь составляем контурные уравнения:

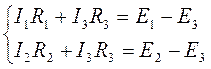
Заменим токи ветвей контурными токами:

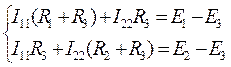
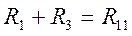- полное сопротивление первого контура.

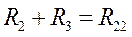- полное сопротивление второго контура.

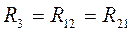- взаимное сопротивление первого и второго контура.

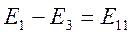- полная ЭДС первого контура.

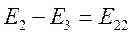- полная ЭДС второго контура, тогда получим:

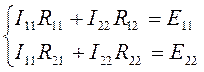
Это и есть система уравнений метода контурных токов.

В общем виде для схемы, имеющей n независимых контуров, эту схему можно записать так:

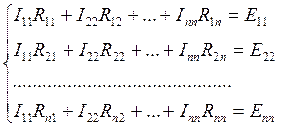
Если индексы у сопротивления одинаковые ( 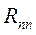), то это полное сопротивление контура, которое определяется суммированием всех сопротивлений, входящих в данный контур.

Если индексы разные, то это взаимные сопротивления контуров, т.е. сопротивление ветви, входящей в оба контура.

Внимание! У взаимных сопротивлений надо помнить правило знаков: если контурные токи, протекающие через взаимные сопротивления имеют одинаковое направление, то перед взаимным сопротивление ставится знак “+”, в противном случае – знак “-”.

В правой части системы (V) стоят полные ЭДС контуров, которые определяются алгебраическим суммирование ЭДС, входящих в данные контур, при этом , если направление ЭДС совпадает с направлением контурного тока (обхода контура), то эта ЭДС берется со знаком “+”, в противном случае – “-”.

Если в схеме имеются источники тока, то необходимо выбрать “мнимый” контур, включающий в себя этот источник, причем источник должен входить во внешнюю ветвь “мнимого” контура. В этом случае контурный ток “мнимого” контура будет равен току источника, который мы знаем. Определяются взаимные сопротивления контуров схемы с “мнимым” контуром 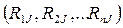и в каждое уравнение системы добавляется произведение тока источника на соответствующее взаимное сопротивление. Уравнения для мнимого контура составлять не надо!

Решив систему контурных токов, мы найдем не реальные токи ветвей, а контурные токи. Теперь необходимо от контурных токов перейти к реальным токам. Это делается следующим образом: если ветвь является внешней и входит только в один контур, то ток в ней равен контурному. При этом, если он совпадает с направлением контурного тока, то берется знак “+”, в противном случае – “-”. Ток взаимной ветви определяется алгебраическим суммированием контурных токов, протекающих через эту ветвь. При этом, если контурный ток совпадает с током ветви, то он берется со знаком “+”, в противном случае – “-”.