Аномальные участки цепи.

Иногда в цепях встречаются такие участки, которые создают затруднение и противоречия при определении количества независимых узловых и контурных уравнений. Пример такого участка цепи показан на рис.2:

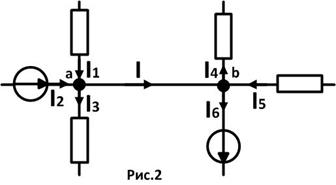
между “узлами” а и b находится “ветвь”, не имеющая никаких элементов и представляющая собой проводник с идеальной проводимостью (R=0). Потенциалы точек a и b равны, поэтому их можно объединить в один узел, который называется “растянутый узел”. Т.е. вместо двух узловых уравнений составляется одно для “растянутого узла ab”, которое в нашем примере имеет вид:

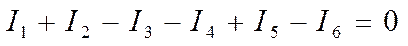
При этом схему можно преобразовать следующим образом(рис.3)

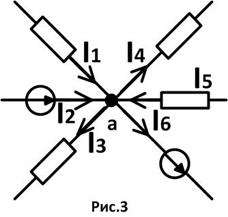
Однако считать узлы “a” и “b” одним “растянутым” узлом можно только в том случае, если нас интересует ток I, протекающий в “пустой” ветви (на рис.3 он пропадает).

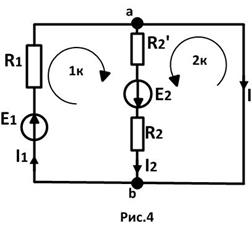
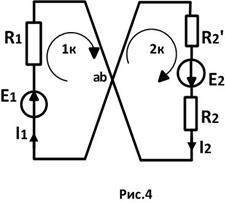
Однако если нас интересует этот ток или он задан в условии задачи, то использовать прием “растянутого узла” нельзя и нужно составлять уравнения для обоих узлов. В этом случае используется термин “пустая ветвь”, которая может входить в один или несколько контуров, быть взаимной ветвью контуров и даже собственной ветвью. (рис.4)

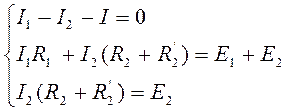
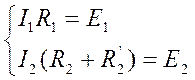
Теория Графов.

Граф цепи или топологическая схема – это схема без изображения элементов в ветвях.

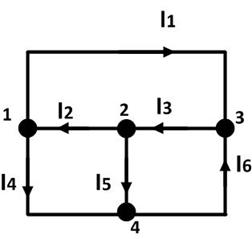
Примечание: часто токи ветвей обозначаются номерами узлов между которыми они протекают. Так, например, ток 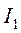можно обозначить как 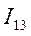или .

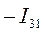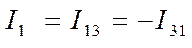
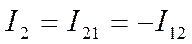
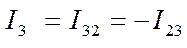
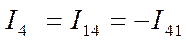
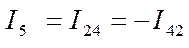
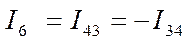
Фигура, которая образуется при соединении всех узлов схемы между собой без образования контуров, называется деревом схемы (рис.6). Число ветвей, входящих в дерево схемы равно числу независимых узловых уравнений.

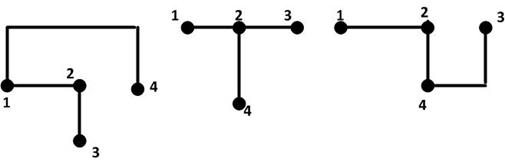
Число ветвей дерева схемы не меняется.

Ветви, включение которых приводит к образованию контура, называются хордами. Число хорд определяет число независимых контурных уравнений.

Разделенная ветвь.

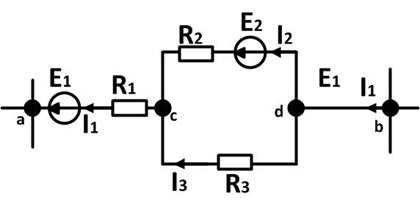
Иногда в цепях встречаются участки, показанные на рис:

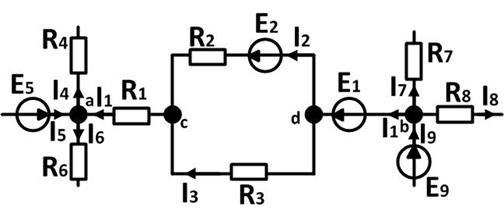
Между узлами a и b находятся три ветви, а не четыре, как может показаться. 2-я и 3-я ветви, включенные параллельно между узлами с и d делят 1-ю ветвь, содержащую 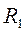и 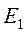, на два участка: 1-й участок – “ac” с 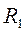, 2-й участок – “db” с 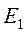. В этом случае “узлы” “c” и “d” являются одним “разделенным узлом” и уравнение составляется только для одного из них.

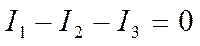
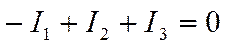
Можно 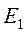перенести к 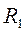и считать d и b растянутым узлом, или перенести 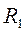к 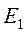и считать растянутым узлом d и c.