Расчет и анализ линейной электрической цепи по законам Кирхгофа.

Как правило, в задачах заданы все ЭДС, сопротивления и источники тока, при этом нужно определить токи в ветвях электрической цепи. Однако бывают и обратные задачи в которых требуется определить при каких значениях ЭДС и источника тока в ветвях будут протекать заданные токи, при этом сопротивления ветвей известны. Есть задача на определение сопротивлений в ветвях при заданных ЭДС и токах в ветвях. Бывают комбинированные задачи, в которых заданы некоторые источники, некоторые сопротивления и некоторые токи ветвей, при этом требуется найти неизвестные токи, ЭДС и сопротивления.

Количество неизвестных должно совпадать с количеством ветвей электрической цепи за исключением ветвей, содержащих источники тока.

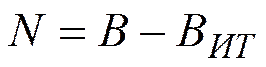
Следовательно, при решении задачи по законам Кирхгофа необходимо составить N уравнений, столько – же, сколько в схеме содержится ветвей без источника тока.

А сколько уравнений нужно взять по 1му и по 2му закону Кирхгофа?

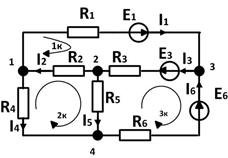Уравнения по 1му закону Кирхгофа проще, поэтому их нужно брать как можно больше (эти уравнения называют еще узловыми). Для схемы, изображенной на рис.1 можно составить 4е уравнение по первому закону Кирхгофа. Но все ли они нужны? запишем уравнения для 1, 2 и 3 узла:

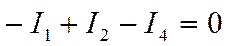
1У

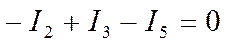
2У

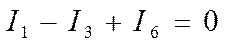
3У

Теперь сложим их левые и правые части:

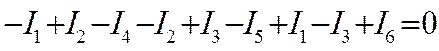
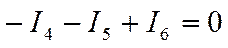или поменяв знаки .

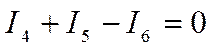Мы получили при этом четвертое уравнение. Т.е. три уравнения для этой схемы несут информацию о четвертом, последнем уравнении, которое называется зависимым. 1,2 и 3е уравнения называются независимыми узловыми уравнениями.

Если рассмотреть другую схему с иным количеством узлов, то для нее будет характерна та же картина: последнее уравнение по 1му закону Кирхгофа можно получить, просуммировав уравнения для других узлов.

Из этого следует, что для решения задачи нужно взять узловых уравнений на единицу меньше количества узлов – у.

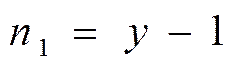
Количество уравнений по 1му закону Кирхгофа - 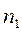на единицу меньше количества узлов – у, содержащихся в цепи. Последнее уравнение – зависимое.

Выбор независимых узловых уравнений произволен, т.е. можно было взять в качестве независимых, уравнения для 2, 3, 4 узлов, или 1,3, 4 и т.д.

Теперь легко определить необходимое количество уравнений по 2му закону Кирхгофа – их называют контурными уравнениями. Если общее количество уравнений – N, а узловых уравнений - 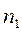, то количество контурных уравнений - 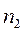определяется, как :

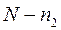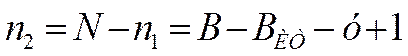
Количество уравнений по 2му закону Кирхгофа равно общему количеству уравнений N минус количество уравнений по 1му закону Кирхгофа .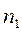

Контура, уравнения которых используются для решения задачи, называются независимыми контурами, а их уравнения – независимыми контурными уравнениями.

Выбор независимых контуров произволен.

Для цепи в нашем примере неизвестных токов – шесть, ветвей без источников тока – шесть, узлов – четыре, независимых узлов – три, независимых узловых уравнений – три, следовательно независимых контуров - 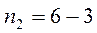. Только для трех контуров нужно составлять уравнения по второму закону Кирхгофа в нашем примере (а всего контуров – семь). При этом не имеет значения какие три контура взять. Возьмем, для примера, 1, 2 и 3 контура. Посмотрим на ветви схемы: мы видим, что 1я ветвь входит только в 1й контур, 4я ветвь – только во 2й контур, а 6я ветвь - только в 3й контур, а 2я, 3я и 5я ветви входят сразу в два контура.

Ветви, входящие в несколько независимых контуров называются взаимными ветвями контуров или смежными ветвями.

Ветви, входящие только в один независимый контур называются внешними или собственными ветвями контуров.

Из примера мы видим, что каждый независимый контур имеет собственную ветвь, т.о. мы можем сформулировать еще одно определение независимого контура:

Независимый контур – это контур, имеющий собственную (внешнюю) ветвь, не входящую ни в один другой контур и принадлежащую только ему.