Основы теории кодирования.

Кодирование. Основные понятия.

Различные методы кодирования широко используются в практической деятельности человека с незапамятных времён. Например, десятичная позиционная система счисления – это способ кодирования натуральных чисел. Другой способ кодирования натуральных чисел – римские цифры, причем этот метод более наглядный и естественный, действительно, палец – I, пятерня – V, две пятерни – X. Однако при этом способе кодирования труднее выполнять арифметические операции над большими числами, поэтому он был вытеснен способом кодирования основанном на позиционной десятичной системой счисления. Из этого примера можно заключить, что различные способы кодирования обладают присущими только им специфическими особенностями, которые в зависимости от целей кодирования могут быть как достоинством конкретного способа кодирования, так и его недостатком.

Широко известны способы числового кодирования геометрических объектов и их положения в пространстве: декартовы координаты и полярные координаты. И эти способы кодирования отличаются присущими им специфическими особенностями.

До XX века методы и средства кодирования играли вспомогательную роль, но с появлением компьютеров ситуация радикально изменилась. Кодирование находит широчайшее применение в информационных технологиях и часто является центральным вопросом при решении самых разных задач таких как:

– представление данных произвольной природы (чисел, текста, графики) в памяти компьютера;

– оптимальная передача данных по каналам связи;

– защита информации (сообщений) от несанкционированного доступа;

– обеспечение помехоустойчивости при передаче данных по каналам связи;

– сжатие информации.

С точки зрения теории информации кодирование — это процесс однозначного сопоставления алфавита источника сообщения и некоторой совокупнос­ти условных символов, осуществляемое по определенному правилу, а код (ко­довый алфавит) — это полная совокупность (множество) различных условных символов (символов кода), которые могут использоваться для кодирования исходного сообщения и которые возможны при данном правиле кодирования. Число же различных кодовых символов составляющих кодовый алфавит называют объемом кода или объёмом кодового алфавита. Очевидно, что объём кодового алфавита не может быть меньше объёма алфавита кодируемого исходного сообщения. Таким образом, кодирование — это преобразование исходного сообщения в совокупность или последовательность кодовых символов, отображающих сообщение, передаваемое по каналу связи.

Кодирование может быть числовым (цифровым) и нечисловым, в зависимости от вида, в котором представлены кодовые символы: числа в какой-либо системе счисления или иные какие-то объекты или знаки соответственно.

В большинстве случаев кодовые символы представляют собой совокупность или последовательность неких простейших составляющих, например, последовательность цифр в кодовых символах числового кода, которые называются элементами кодового символа. Местоположение или порядковый номер элемента в кодовом слове определяется его позицией.

Число элементов символа кода, используемое для представления одного символа алфавита исходного источника сообщений, называют значностью кода. Если значность кода одинакова для всех символов алфавита исходного сообщения, то код называют равномерным, в противном случае — неравномерным. Число элементов входящих в кодовый символ иногда называют дли­ной кодового символа.

С точки зрения избыточности все коды можно разделить на неизбыточные коды и избыточные. В избыточных кодах число элементов кодовых символов может быть сокращено за счет более эффективного использования оставших­ся элементов, в неизбыточных же кодах сокращение числа элементов в кодо­вых символах невозможно.

Задачи кодирования при отсутствии помех и при их наличии существенно различны. Поэтому различают эффективное (статистическое) кодирование и кор­ректирующее (помехоустойчивое) кодирование. При эффективном кодировании ставится задача добиться представления символов алфавита источника сообщений минимальным числом элементов кодовых символов в среднем на один символ алфавита источника сообщений за счет уменьшения избыточности кода, что ведет к повышению скорости передачи сообщения. А при корректирующем (помехоустойчивом) кодировании ставится задача снижения вероятности ошибок в передаче символов исходного алфавита путем обнаружения и исправления ошибок за счет введения дополнительной избыточности кода.

Отдельно стоящей задачей кодирования является защита сообщений от несанкционированного доступа, искажения и уничтожения их. При этом виде кодирования кодирование сообщений осуществляется таким образом, чтобы даже получив их, злоумышленник не смог бы их раскодировать. Процесс такого вида кодирования сообщений называется шифрованием (или зашифровкой), а процесс декодирования – расшифрованием (или расшифровкой). Само кодированное сообщение называют шифрованным (или просто шифровкой), а применяемый метод кодирования – шифром.

Довольно часто в отдельный класс выделяют методы кодирования, которые позволяют построить (без потери информации) коды сообщений, имеющие меньшую длину по сравнению с исходным сообщением. Такие методы кодирования называют методами сжатия или упаковки данных. Качество сжатия определяется коэффициентом сжатия, который обычно измеряется в процентах и который показывает на сколько процентов кодированное сообщение короче исходного.

При автоматической обработке информации с использованием ЭВМ как правило используют числовое (цифровое) кодирование, при этом, естествен­но, возникает вопрос обоснования используемой системы счисления. Действительно, при уменьшении основания системы счисления упрощается алфавит элементов символов кода, но происходит удлинение символов кода. С другой стороны, чем больше основание системы счисления, тем меньшее число разрядов требуется для представления одного символа кода, а, следовательно, и меньшее время для его передачи, но с ростом основания системы счисления существенно повышаются требования к каналам связи и техническим средствам распознавания элементарных сигналов, соответствующих различным элементам символов кода. В частности, код числа, записанного в двоичной системе счисления в среднем приблизительно в 3,5 раза длиннее десятичного кода. Так как во всех системах обработки информации приходится хранить большие информационные массивы в виде числовой информации, то одним из существенных критериев выбора алфавита элементов символов числового кода (т.е. основания используемой системы счисления) является минимизация количества электронных элементов в устройствах хранения, а также их простота и надежность.

При определении количества электронных элементов требуемых для фиксации каждого из элементов символов кода необходимо исходить из практически оправданного предположения, что для этого требуется количество простейших электронных элементов (например, транзисторов), равное основанию системы счисления a. Тогда для хранения в некотором устройстве n элементов символов кода потребуется M электронных элементов:

M = a·n. (2.1)

Наибольшее количество различных чисел, которое может быть записано в этом устройстве N:

N = aⁿ .

Прологарифмировав это выражение и выразив из него n получим:

n = ln N / ln a.

Преобразовав выражение (2.1) к виду

M = a ∙ ln N / ln a (2.2)

можно определить, при каком основании логарифмов a количество элементов M будет минимальным при заданном N. Продифференцировав по a функцию M = f(a) и приравняв её производную к нулю, получим:

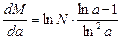= 0.

Очевидно, что для любого конечного a

ln N / ln² a ≠ 0

и, следовательно,

ln a -1 = 0,

откуда a = e ≈ 2,7.

Так как основание системы счисления может быть только целым числом, то а выбирают равным 2 или 3. Для примера зададимся максимальной емкостью устройства хранения N=10⁶ чисел. Тогда при различных основаниях систем счисления (а)количество элементов (M)в таком устройстве хранения будет, в соответствии с выражением (2.2), следующие (Таблица 2.1):

Таблица 2.1.

Следовательно, если исходить из минимизации количества оборудова­ния, то наиболее выгодными окажутся двоичная, троичная и четверичная системы счисления, которые близки по этому параметру. Но так как техническая реализация устройств, работающих в двоичной системе счисления, значительно проще, то наибольшее распространение при числовом кодировании получили коды на основе системы счисления по основанию 2.