Общая математическая модель плоского произвольного движения судна

При определении кинетической энергии системы «судно-жидкость» и составлении уравнений движения судна обычно используют следующие упрощающие допущения:

- жидкость считается несжимаемой, идеальной и безграничной, либо имеющей твердые неподвижные границы;

- предполагается, что все движение жидкости вызвано только движением судна, тогда, движение жидкости является безвихревым, и существует потенциал скоростей;

- вместо движения реального судна в жидкости со свободной поверхностью рассматривается движение погруженной части судна, дублированной (зеркально отраженной) относительно плоскости ватерлинии, твердые границы потока также отображаются относительно этой плоскости;

- волнообразование на свободной поверхности исключается из рассмотрения;

- наклонения судна в плоскости шпангоута малы и не влияют на инерционные силы и на гидродинамические характеристики (ГДХ);

- движение судна является плоским, крен и вертикальное смещение при движении отсутствуют, изменение скорости судна в процессе маневра не влияет на его дифферент и среднюю осадку;

- все ГДХ судна при неустановившемся движении в каждый момент времени совпадают с ГДХ судна, совершающего установившееся движение с теми же элементами (скоростью угловой скоростью, углом дрейфа), т.е. используется гипотеза стационарности, обоснованная К.К.Федяевским.

Математическая модель движения судна формируется в подвижной, связанной с судном прямоугольной системе координат ХGУ с началом G в центре масс судна.

Эта система в несколько упрощенном варианте имеет вид:

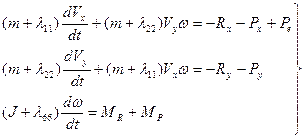(22)

Первое уравнение системы (22) характеризует движение судна по оси X при разгоне и торможении, поэтому его решения позволяют оценивать инерционно-тормозные характеристики судов. Решения второго уравнения, описывающего закономерности поперечного смещения, позволяют получить зависимости для дрейфа судна на циркуляции и под влиянием ветра. Третье уравнение, характеризующее угловое движение используется при оценке управляемости судов.

В левых частях системы (22) стоят инерционные силы и моменты: в первых двух уравнениях – соответствующие проекции силы инерции и центробежной силы, а в третьем уравнении – инерционный момент относительно вертикальной оси. В правых частях стоят неинерционные силы и моменты, записанные в общем виде. Все неинерционные силы и моменты, входящие в систему (22), выражаются нелинейными зависимостями от поступательной и угловой скоростей, поэтому данная система не может быть проинтегрирована до конца при строгой постановке.

Для того чтобы получить отдельные приближенные решения этой системы, обычно используют различные допущения и упрощения. Особенно широко применяются допущения, введенные К.К.Федяевским. Так, принятое им разделение неустановившегося движения судна на короткопериодическое изменение угловой скорости и угла дрейфа и длиннопериодическое изменение линейной скорости судна позволило отделить решение первого уравнения системы от остальных двух и получить таким путем приближенное решение для всей системы уравнений. Этот метод до настоящего времени используется в практике расчетов управляемости судов. Допущение о квазистационарности вязкостных составляющих гидродинамических сил, действующих на корпус судна дало возможность пренебречь в правой части уравнений управляемости судна производными параметров движения и тем самым существенно упростить всю систему уравнений.

Бурное развитие вычислительной техники, ставшей широко доступной для исследователей в последние десятилетия, изменило генеральное направление в развитии теории управляемости. Аналитические методы исследования в значительной мере уступили место численным методам. Решение уравнений движения судна при полном учете всех их членов перестало быть непреодолимой проблемой.

Наибольшую сложность стало представлять достоверное определение сил и моментов, входящих в уравнения движения судна, в зависимости от параметров движения. Именно на этом и были сосредоточены усилия большого числа российских и зарубежных ученых. С этой целью были созданы установки нового типа, так называемые планарные механизмы (РММ), позволяющие производить гармонический анализ сил и моментов, действующих на модель судна при произвольном криволинейном движении, и позволившие вплотную подойти к решению проблемы квазистационарности, Произведены обширные исследования физической природы действующих на корпус судна сил, испытаны масштабные серии моделей.

В настоящее время для исследования управляемости наиболее рациональным считается раздельное изучение, действующих на корпус судна, и сил, развиваемых ДРК , и сил их взаимодействия.

Рассмотрим подробнее особенности действующих сил и способы их определения