Свойства определителей.
Определители 1, 2, 3-го порядка.
Определение 1. Определителем квадратной матрицы А называется число, которое обозначается 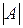 , detA, ∆
, detA, ∆
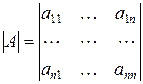 .
.
Порядок матрицы является и порядком определителя.
Элементы 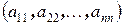 образуют главную диагональ, а элементы
образуют главную диагональ, а элементы 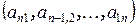 – побочную.
– побочную.
Вычисление определителей 1, 2, 3-го порядка.
1). Определитель первого порядка (п=1) равен своему элементу: 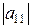 =
= 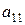 .
.
Пример. 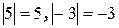 .
.


|
|
|
|

|
|
|
|
|

|

|
|
|
|
 2). Определитель второго порядка (п=2) равен произведению элементов главной диагонали минус произведение элементов побочной диагонали:
2). Определитель второго порядка (п=2) равен произведению элементов главной диагонали минус произведение элементов побочной диагонали: 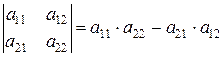 , т.е.
, т.е.
 Пример.
Пример.

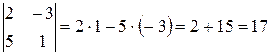 .
.
3). Определитель третьего порядка (п=3) можно вычислить по правилу треугольников (правилу Саррюса):

т.е. 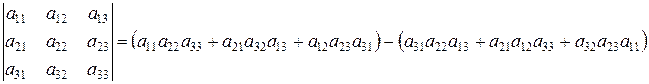
Пример.
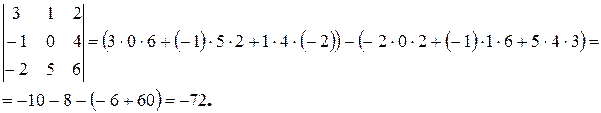
Определители более высоких порядков вычисляются с помощью свойств определителей.
Свойства определителей.
1°. Значение определителя не меняется при транспонировании
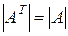 .
.
Пример.
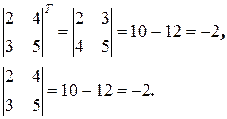
2°. При перестановке двух строк или двух столбцов определитель меняет знак.
Пример.
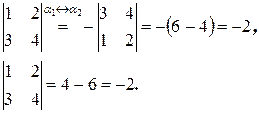
3°. Определитель, имеющий строку (или столбец), состоящую из нулей, равен нулю.
Пример.
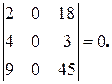
4°. Общий множитель строки или столбца можно выносить за знак определителя.
Пример.
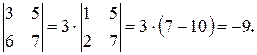
5°. Если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или другого столбца), умноженные на одно и то же число, то значение определителя не изменится.
Пример.
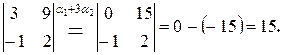
6°. Определитель, имеющий пропорциональные строки (или столбцы) равен нулю.
Пример.
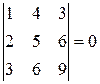 , т.к. соответствующие элементы первого и третьего столбцов пропорциональны.
, т.к. соответствующие элементы первого и третьего столбцов пропорциональны.
7°. Если каждый элемент некоторой строки (столбца) можно представить в виде суммы двух слагаемых, то такой определитель равен сумме двух определителей такого вида:
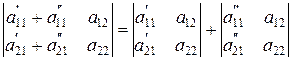 .
.
Пример.
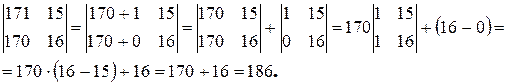
| <== предыдущая лекция | | | следующая лекция ==> |
| Учет нематериальных активов | | | Влияние условий эксплуатации на изменение технического состояния автомобилей |
Дата добавления: 2020-03-17; просмотров: 649;











