Оптимальное проектирование РЭС. Введение в проблему оптимального проектирования

Любые системы автоматизированного проектирования (САПР) основаны на автоматизации трех видов процедур:

- синтез;

- анализ;

- принятие решений.

Наименее автоматизированной является процедура принятия решений, степень их автоматизации существенно повышается в случае, если для принятия решений используются методы оптимизации.

Первые разработки по методам оптимизации появились в середине 30-х г.г. XIX века и были связаны с принятием оптимальных решений в экономических задачах.

Развитие САПР в начале 60-х г.г. в нашей стране сразу было ориентировано на применение методов оптимизации, и наши отечественные программные комплексы, нашедшие в тот период применение в промышленности, включали в качестве обязательных оптимизационные процедуры. Унифицированные программные комплексы, которые разрабатывались на Западе, обычно модули оптимизации не включали, но сложившиеся условия на рынке программной продукции и те изменения, которые произошли в 90-х г.г., привели к ориентации на зарубежные программные комплексы САПР.

Подключение в 90-е г.г. российских специалистов к совершенствованию этих программных комплексов привело к появлению в их структуре модулей оптимизации.

При формировании оптимизационной модели следует учитывать три составляющие:

Требования к параметрам объекта проектирования.

Любой объект характеризуется параметрами x_j, 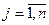. В техническом задании на параметры обычно накладываются граничные требования, то есть задается минимальная граница 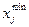и максимальная 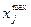, тогда в формализованном виде граничное условие записывается следующим образом:

.

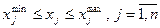Наличие модели, позволяющей рассчитывать показателей объекта проектирования при заданных параметрах.

Помимо параметров, есть показатели объекта проектирования y_j, 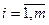. В качестве показателей объекта проектирования могут быть надежность, стабильность, быстродействие, показатели экологического характера и т. п., причем должна быть известна зависимость показателя объекта проектирования от его параметров:

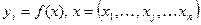. (5.1)

Методы оптимизации построены таким образом, что функцию f не обязательно знать в аналитическом виде. Для решения задач оптимизации могут использоваться численные методы.

3. Требования к показателям объекта проектирования.

Существует два вида требований к показателям объекта проектирования:

а) экстремальные требования – используются, когда необходимо достичь наилучшего значения показателя (максимального или минимального):

;

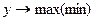б) граничные требования – обычно устанавливаются на показатель в техническом задании:

.

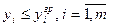5.2. Классификация задач оптимизации и методы их решения

Для применения методов оптимизации реальную оптимизационную модель приводят к стандартизованной форме:

,

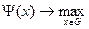где 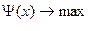- критерий (целевая функция оптимизации);

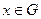- множество ограничений.

При этом множество G в стандартизованном виде:

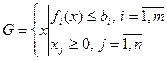. (5.2)

Из множества оптимизационных моделей выделяют:

1) модели без ограничений

.

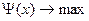Результатом решения этой задачи является определение некоторого х*, которое называется оптимальным решением.

Когда применяются методы оптимизации, используются не аналитические, а пошаговые решения;

2) модели с ограничениями

их принято называть моделями математического программирования:

.

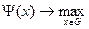Этот класс разбивается на ряд подклассов:

а) задачи линейного программирования -

в этом случае целевая функция 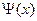и все функции ограничений 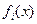являются линейными.

Задача линейного программирования (ЗЛП) записывается в следующем виде:

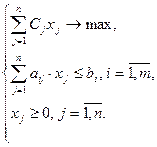; (5.3)

б) задачи нелинейного программирования -

если целевая функция 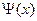либо одна из функций ограничений 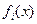является нелинейной, то мы имеем дело с задачей нелинейного программирования.

в) задачи дискретного программирования (ЗДП) -

в целом ряде случаев на параметры накладываются особые ограничения, связанные с тем, что они могут принимать только дискретные уровни из некоторого набора

.

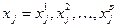Например: х_j=1,2,…5.

Как подкласс в ЗДП выделяются задачи булевого программирования.

В этом случае

;

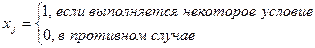г) задачи динамического программирования -

в этом случае целевая функция 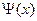зависит не только от параметров, но и от времени:

;

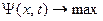3) задачи оптимизации с неопределенностями.

Здесь существует два вида неопределенностей:

а) неопределенность математического описания -

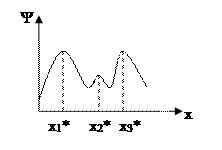в этом случае целевая функция либо имеет точки разрыва 1-го рода, либо является многоэкстремальной.

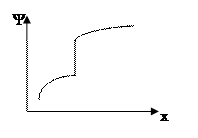Рис. 5.1 – Графики функций с неопределенностью математического описания

б) неопределенность в выборе цели - в этом случае экстремальные требования предъявляются не к одному показателю, а к нескольким.

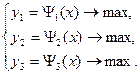(5.4)

Такая задача оптимизации называется многоэкстремальной.

5.2.1. Задачи оптимизации без ограничений

Математическая запись задачи оптимизации без ограничений:

.

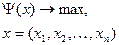В математическом анализе для исследования функций многих переменных на экстремум используются необходимые и достаточные условия экстремума и условие для определения типа экстремума.

Для случая задач многомерной оптимизации

.

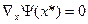Это приводит к системе алгебраических уравнений:

,

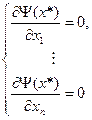где х* - вектор, характеризующий точку экстремума .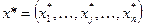

Но в ряде случаев мы не имеем математической модели, а только при заданном значении х мы можем определить значение функции. Кроме того, система может быть нелинейной. Следовательно, решение будет получено приближенно.

В связи с тем, что на практике во многих случаях отсутствует аналитическая модель целевой функции, а решение системы алгебраических уравнений приходится находить приближенными методами, основное распространение при решении задач оптимизации получили численные методы. Основанные на непосредственном понимании экстремума как наибольшего и наименьшего значения целевой функции.

Структура численных методов оптимизации

Численные методы оптимизации основаны на итерационном (пошаговом) принципе поиска точки экстремума. Они состоят из трех компонентов:

1) задание начальных условий

Начальные условия задаются проектировщиком, исходя из технических, логических, физико-химических требований. Они характеризуют значение вектора оптимизационных переменных на первом шаге.

k – номер шага (итерации),

k = 1,2,3,…

Начальное условие на первом шаге:

.

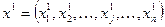Эти условия задаются извне (исходя из технических, логических, физико-химических условий), на практике (когда имеем дело с реальными объектами) эти условия фундаментально обосновываются.

2) алгоритм определения значения оптимизируемой переменной на (k+1)-м шаге

x^k – известно,

x^k+1 – требуется определить.

Алгоритм строится по следующему признаку: формируется функция от оптимизируемой переменной на k-м шаге и зависящая от функции 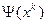. В этом случае нас интересует не просто переход от значения x^k и x^k+1, а переход, соответствующий некоторому условию локального улучшения (УЛУ):

.

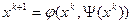3) правило останова

Самое простое правило останова k≤K, где К – заданное число итераций.

Может также использоваться условие, основанное на том. Что по мере приближения к точке экстремума все алгоритмы работают таким образом, что (x^k+1 - x^k) начинает уменьшаться:

.

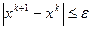В связи с условием многомерной оптимизации:

.

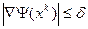Когда есть все три составляющие, численные методы приводят к поиску х*, но с некоторой ошибкой.

Различные подходы и методы решения задач оптимизации связаны с поиском определенного компромисса между скоростью и точностью поиска оптимального значения переменной х.

Методы решения задач оптимизации без ограничений

В простейших случаях (когда имеет дело с одномерной оптимизацией) действуют методы одномерного унимодального поиска. К их числу относятся:

- метод дихотомии;

- метод Фибоначчи;

- метод золотого сечения;

- обобщенный метод Фибоначчи.

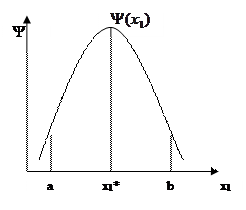
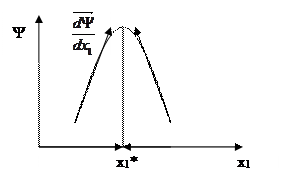
Рис. 5.2 - Графическая интерпретация методов одномерного унимодального поиска

Данные методы основаны на принципе пошагового движения с целью сокращения зоны (внутри которой находится искомое решение х₁*) от начального условия [a,b] и приближения к экстремуму на основе соответствующего правила останова (рис. 5.2). Описание методов одномерной оптимизации будет дано в п. 5.4.

В данном подразделе рассмотрим более подробно градиентные методы оптимизации, которые основаны на геометрическом механизме движения из одной точки пространства в другую. Этот механизм связан с выбором двух составляющих:

направление движения;

величина шага, с которым мы движемся в этом направлении

,

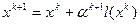где 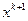- х от (k+1)-й итерации;

l – вектор, указывающий направление движения их точки ,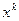

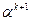- величина шага в этом направлении.

В качестве направления движения в градиентных алгоритмах принимается направление вектора градиента.

Следовательно, градиент имеет вид:

.

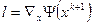Выбор градиента обоснован тем, что только градиент показывает, движемся ли мы в сторону экстремума или в противоположном направлении.

Вектор производной (в многомерном случае вектор градиента) изображен на рис. 5.3:

Рис. 5.3 – Графическая интерпретация градиентных методов оптимизации

Величину шага 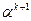можно выбирать произвольно. Так как можно 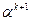и l можно изменять, выражение ( ) обладает двумя степенями свободы.

В целом различают три типа численных методов оптимизации:

1) методы нулевого порядка – методы, использующие только информацию о значении целевой функции (методы одномерного унимодального поиска);

2) методы первого порядка – методы, дополнительно использующие информацию о первых производных целевой функции;

3) методы второго порядка – методы, дополнительно использующие информацию о вторых производных целевой функции.

Исходя из этой классификации, методы выбора величины шага α разделяются на два класса:

метод, использующий информацию о целевой функции и ее первых производных;

метод, использующий дополнительно информацию о вторых производных целевой функции.

Рассмотрим подход к выбору величины шага для первого класса методов. При переходе от значения оптимизируемой переменной х^k к х^k+1 :

величина шага α;

определяется значение х, равное ;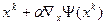

проверяется условие локального улучшения

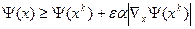, где .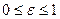

Если до точки экстремума далеко, выражение под знаком модуля должно быть большим, чтобы значение 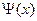значительно превосходило значение 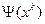. По мере приближения к экстремуму выражение под знаком модуля стремится к нулю, это заставляет в зоне экстремума делать малые шаги.

Таким образом, второе слагаемое в условии локального улучшения является регулятором скорости и точности поиска экстремума.

если условие локального улучшения выполняется, то величина шага 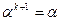. В противном случае осуществляется дробление шага 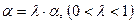до тех пор, пока не будет выполнено условие локального улучшения.

Второй класс градиентных алгоритмов основан на использовании информации о вторых производных и принцип их построения связан с приближенным методом Ньютона определения дифференциала аргумента

,

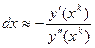на котором и основан градиентный алгоритм Ньютона:

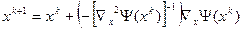, (5.5)

где 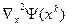- матрица вторых производных целевой функции на k-й итерации.

В случае если функция 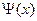является квадратичной, то алгоритм Ньютона позволяет определить оптимальное значение х за один шаг, не зависимо от заданных начальных условий. Таким образом, если функция строго квадратичная, то алгоритм Ньютона работает оптимально, то есть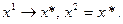

Для функций, отличных от квадратичных разработан целый ряд квазиньютоновских алгоритмов, которые основаны на двух механизмах:

1. Вводится регулируемый шаг α, используемый в формуле ( ). Шаг α выбирается таким образом, чтобы в локальной окрестности этого шага аппроксимировать оптимизируемую функцию в квадратичной форме.

2. Приближенное пошаговое определение элементов обратной матрицы вторых производных через приращения первых производных.

Самым сложным, но самым эффективным методом из числа градиентных методов является метод Давидона-Флетчера-Пауэлла.

5.2.2. Задачи оптимизации с ограничениями

Штрафная функция Лагранжа

Задача оптимизации с ограничениями представляется классом оптимизационных моделей математического программирования.

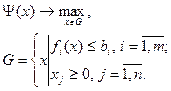(5.6)

Основным подходом решения задач математического программирования является подход, основанный на переходе от решения задачи с ограничениями к задаче без ограничений, для которой имеются численные методы решения.

Существуют разные способы такого перехода, но наиболее распространенным является переход, связанный с формированием функции Лагранжа. В этом случае структура функции Лагранжа имеет следующий вид:

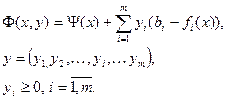(5.7)

Переменные векторы у принято называть переменными функций Лагранжа, штрафными переменными, переменными двойственной задачи. Наиболее часто используется название «штрафные переменные».

Необходимость поиска компромисса между максимизацией целевой функции и удовлетворением ограничений приводит к следующим экстремальным требованиями по отношению к функции Лагранжа:

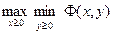. (5.8)

Для каждого из значений 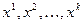находится значений функции Лагранжа

.

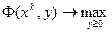Затем решается задача минимизации по 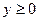, и в результате этого решения находятся пары (х_k, y_k). Эти значения подставляются в штрафную функцию Лагранжа и среди этих значений находится максимальное, которое и будет оптимальным решением задачи (х*, y*).

Задача максимина функции Лагранжа точно соответствует исходной задаче математического программирования. Такая задача называется прямой задачей оптимизации функции Лагранжа.

Двойственная задача функции Лагранжа. Понятие Седловой точки

Двойственная задача функции Лагранжа представляет собой задачу минимакса:

.

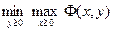Для решения двойственной задачи функции Лагранжа необходимо:

зафиксировать значения ;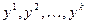

для каждого из значений у решить задачу 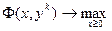и найти пары (х_k, y_k);

подставить эти значения в штрафную функцию Лагранжа

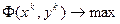
и выбрать из этого решения оптимальное (х*, y*).

Точку, представляющую собой пару векторов 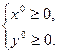будем называть седловой точкой функции Лагранжа, если она является оптимальным решением как прямой, так и двойственной задач оптимизации функции Лагранжа.

Понятие седловой точки является важным в теории оптимизации в силу следующего основного утверждения: если пара векторов 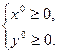является Седловой точкой функции Лагранжа, то вектор 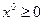представляет собой оптимальное решение исходной задачи математического программирования.

Таким образом, алгоритм решения задач оптимизации с ограничениями выглядит следующим образом:

- переход от исходной задачи математического программирования к задаче оптимизации штрафной функции Лагранжа;

- поиск седловой точки функции Лагранжа;

- определение оптимального решения х* как значения вектора х⁰ ( ).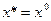

5.2.3. Задачи структурной оптимизации

Методы структурной оптимизации в качестве основного признака этого класса задач учитывают комбинаторный характер формирования проектных вариантов. Формализованный подход к учёту комбинаторного характера структурного синтеза достигается на основе методов дискретной оптимизации, так как варьируемые компоненты структуры заданы на дискретном множестве. Их решение основано на методах дискретного (целочисленного, булевого) и динамического программирования.

Применение методов дискретного программирования связано с вычислительной сложностью переборных задач, к которым сводятся задачи структурной оптимизации. Переборные задачи разделяются на классы. По крайней мере один из параметров переборной задачи не ограничен. Индивидуальные задачи различаются исходными данными, значениями численных параметров условий задачи.

Одной из известных задач структурной оптимизации является задача о ранце. Эта задача заключается в определении наиболее приемлемых параметров (размеров) ранца. Многомерная задача о ранце является задачей целочисленного линейного программирования с булевыми переменными:

;

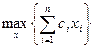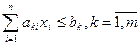; (5.9)

.

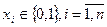В частном случае при m = 1 данная задача сводится к одномерной задаче о ранце:

,

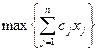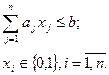(5.10)

Решение целочисленных задача сводится к поиску экстремальных значений параметров на допустимом множестве ограничений. В качестве методов решения используются методы математического программирования (линейного, нелинейного, выпуклого). Задача о ранце решается методами целочисленного линейного программирования, к которым относятся метод округления, метод отсечения, метод ветвей и границ.

5.2.4. Задачи дискретного программирования

Задача параметрической оптимизации с дополнительным условием, чтобы управляемые параметры x принимали только дискретные значения, называется задачей дискретной оптимизации. Если все управляемые параметры x_j, 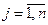, принимают только целочисленные значения, то задача дискретной оптимизации становится задачей целочисленного линейного программирования (ЦЛП):

(5.11)

(5.12)

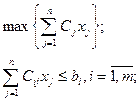
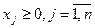; (5.13)

x_k, k = 1, p –целые числа. (5.14)

Предположим, что область допустимых решений D задачи линейного программирования (5.11) – (5.13) представляет собой выпуклое ограниченное множество. Тогда область допустимых решений D_ц задачи ЦЛП (5.11) – (5.14) будет представлять собой дискретное множество точек x_ц с целочисленными координатами, которые принадлежат области D (D_ц Ì D).

Оптимальное решение задачи линейного программирования (5.11) – (5.13) обозначим вектором x (D, c), а оптимальное целочисленное решение задачи ЦЛП (5.11) – (5.14) – вектором x (D_ц, c).

Задача ЦЛП благодаря условию целочисленности отличается от задачи линейного программирования следующими свойствами:

максимальное значение линейной формы в задаче ЦЛП меньше, чем максимальное значение этой же линейной формы в задаче ЛП:

(c^T,x(D_ц,c)) £ (c^T, x(D,c));

оптимальное решение задачи ЦЛП x (D_ц,c) может ноходиться и внутри области допустимых решений D (в то время как в задаче ЛП оптимальное решение x(D, c) достигается только в крайних точках многогранника условий D);

в задаче ЦЛП, кроме глобального максимума, могут существовать решения, которые являются локальными максимумами по отношению к соседним точкам решётки D_ц;

в задаче ЦЛП оптимальное решение может содержать все n управляемых переменных с положительным знаком, в то время как в невырожденной задаче ЛП число строго положительных переменных равно числу линейных ограничений (5.12).

Задачи ЦЛП могут быть решены с использованием метода округления, метода отсечения, метода ветвей и границ.

5.2.5. Задачи линейного программирования

Постановка и свойства задач линейного программирования

Задача выпуклого программирования называется задачей линейного программирования (ЛП), если критерий оптимальности и ограничения являются линейными функциями от управляемых переменных x:

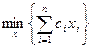, (5.15)

при условии, что

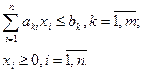(5.16)

Для векторно-матричной записи задачи ЛП введём следующие обозначения:

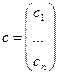- вектор коэффициентов критерия оптимальности;

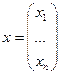- вектор управляемых переменных;

A = {a_ij} – матрица коэффициентов левых частей ограничений размерностью m x n;

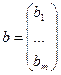- вектор значений правых частей ограничений.

В зависимости от формы записи ограничений для задачи ЛП можно выделить следующие её типы:

Задача ЛП с симметричными ограничениями (m = 0, p = n):

min(c^T, x); (5.17)

Ax £ b; (5.18)

x ³ 0. (5.19)

Задача ЛП в канонической форме (s = 0, p = n):

min(c^T, x); (5.20)

Ax = b;

x ³ 0.

Задача ЛП в сопряжённой форме (m = 0, p = 0):

min(c^T, x); (5.21)

Ax £ b.

Любую из перечисленных форм записи можно привести к любому другому виду с помощью элементарных преобразований. При рассмотрении методов вычисления задач ЛП будет использоваться каноническая форма записи.

Рассмотрим геометрическую интерпретацию задачи ЛП, изображённую на рис. 5.4 [1,7]. На рисунке приведён случай с двумя управляемыми параметрами n=2. Заштрихованы полуплоскости значений параметров, не разрешённых ограничениями. Из рисунка видно, что каждое ограничение выделяет полуплоскость (при n ³ 3 - полупространство) разрешённых значений, а все ограничения вместе определяют область допустимых значений параметров. Эта область всегда является выпуклым многоугольником (при D ³ 3 – выпуклым многогранником).

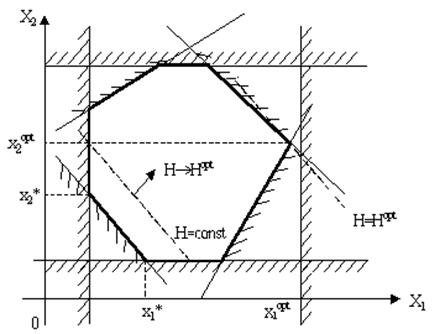
Рисунок 5.4 – Геометрическая интерпретация задачи ЛП.

Уравнение Н = 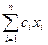при Н = const представляет собой уравнение гиперплоскости в n-мерном пространстве управляемых параметров. На рис.5.4 при n = 2 она представляет собой линию. Изменение значения H при изменении управляемых параметров соответствует параллельному перемещению линии уровня. На рисунке показано направление перемещения с целью оптимизации Н при c_i<0. Конечное положение перемещаемой кривой обозначено на рисунке как H = H^opt. В этом положении линия уровня имеет с областью возможных решений одну общую точку в одной из её вершин. Координаты этой вершины можно найти из совместного решения уравнения двух границ (j=3 и j=4).

Если в критерии оптимальности c_i>0, то для минимизации функции движение необходимо осуществлять в сторону противоположную указанной на рис 1 стрелкой. В более общем случае решение ищут среди базисных решений, которыми называются координаты точек пересечения каждых D граничных гиперплоскостей.

Предположим, что система ограничений задачи ЛП (5.17) – (5.19) совместна, т.е. область допустимых решений D не является пустым множеством.

Точка x*Î D называется крайней точкой выпуклого множества D, если не существует точек x¹, x² Î D, x¹ ¹ x² таких, что крайняя точка может быть выражена через них в виде выпуклой комбинации:

ax¹ + (1-a)x², 0<a<1. (5.22)

Геометрическая интерпретация приведённого определения означает, что точка xÎD является крайней точкой выпуклого множества D только в том случае, если оно не принадлежит ни одному из отрезков, целиком лежащих в этом множестве.

Сформулируем условие, гарантирующее наличие крайних точек в выпуклом многограннике (5.18) – (5.19): для того чтобы точка x = (x₁ … x_n) являлось крайней точкой выпуклого многогранника условий задачи ЛП:

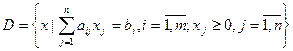, (5.23)

необходимо и достаточно, чтобы среди условий (5.18) – (5.19) нашлось n линейно независимых ограничений, которым эта точка удовлетворяет как точным равенствам, т.е. (n-m) управляемых переменных x_j обращается в нуль.

Геометрическая интерпретация этого утверждения заключается в том, что каждая крайняя точка xÎD является пересечением не мене чем n независимых гиперплоскостей. Следовательно, число крайних точек выпуклого многогранника условий (5.23) является конечным, равным числу сочетаний из (n+m) по n (cⁿ_n+m).

Задача ЛП в канонической форме (5.17) – (5.19) в векторной записи имеет следующий вид:

min(c^T, x); (5.24)

x₁A₁ + x₂A₂ + … + x_nA_n = b; (5.25)

x ³ 0, (5.26)

где 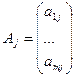- j-й вектор условий задачи ЛП.

На равенство (5.25) можно смотреть как на разложение вектора ограничений b по векторам условий A_j, 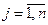с коэффициентами разложения x_j, 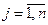. Это позволяет сформулировать условие того, что точка xÎD является крайней точкой.

Для того, чтобы точка x = (x₁ … x_n) была крайней точкой выпуклого многогранника условий (5.23), необходимо и достаточно, чтобы векторы условий A_j, соответствующие её положительным компонентам (x_j > 0), были линейно-независимы. Крайняя точка задачи ЛП называется невырожденной, если она содержит ровно m положительных координат x₁.

Число крайних точек выпуклого многогранника условий – конечно, поэтому область допустимых решений D задачи ЛП совпадает с совокупностью точек x, являющихся выпуклой комбинацией её крайних точек:

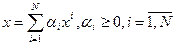; (5.27)

,

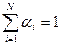где xⁱ, 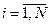- крайние точки выпуклого многогранника условий (5.23);

N – общее число крайних точек.

Относительно оптимального решения x*ÎD задачи ЛП можно сформулировать следующие утверждения:

Линейная форма (5.17) достигает своего минимального значения в крайней точке выпуклого многогранника условий (5.23). Если линейная форма (5.17) принимает минимальное значение более чем в одной крайней точке, то она достигает этого же значения в любой точке, являющейся выпуклой линейной комбинацией этих крайних точек.

Если линейная форма (5.17) достигает минимального значения в единственной крайней точке x*ÎD, то этот минимум является глобальным минимумом.

Разрешимость задач линейного программирования

Задача ЛП – разрешима, если для неё существует оптимальное решение x*ÎD. Для разрешимости задачи линейного программирования необходимо и достаточно, чтобы она обладала хотя бы одним допустимым решением xÎD, а линейная форма была ограничена снизу в области допустимых решений D.

Рассмотрим геометрическую интерпретацию математических свойств задачи ЛП на примере двухмерной задачи с симметрическими ограничениями:

,

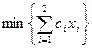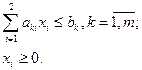
(5.28)

В зависимости от коэффициентов линейной формы c_i и структуры области допустимых решений D при решении задач ЛП могут возникнуть следующие ситуации:

Задача ЛП имеет единственное оптимальное решение. В этом случае опорная прямая 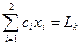касается выпуклого многоугольника D в одной крайней точке x* = x₃ (рис.5.5, а).

Задача ЛП имеет множество оптимальных решений. В этом случае опорная прямая 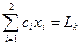проходит через две крайние точки x₂ и x₃, множество оптимальных решений совпадает с ребром [x₂, x₃] (рис.5.5, б).

Задача ЛП имеет неограниченное оптимальное решение. Область допустимых решений D является неограниченным выпуклым многогранником, а функции 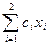является неограниченной функцией на этом многограннике – значение линейной формы стремиться к минус бесконечности (рис.5.6, а).

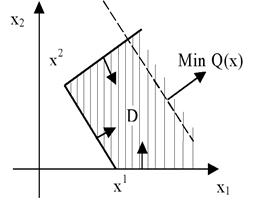
Задача ЛП неразрешима (не имеет оптимального решения). Область допустимых решений D является пустым множеством, так как ограничения задачи ЛП являются несовместными условиями (рис.5.6, б).

б

а

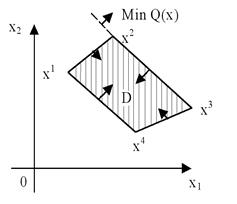
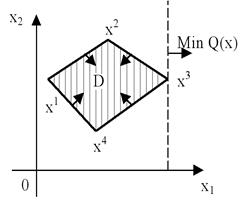
Рисунок 5.5 – Типы оптимальных решений задачи ЛП:

а – задача имеет единственное оптимальное решение x^x;

б – задача имеет бесконечное множество оптимальных решений.

	в		г

Рисунок 5.6 – Типы оптимальных решений задачи ЛП:

а – задача имеет неограниченное оптимальное решение;

б – задача неразрешима.

Запишем данную задачу в матричной форме:

max(c^T, x); (5.29)

Ax £ b; (5.30)

x ³ 0. (5.31)

Эта задача называется прямой задачей ЛП.

Двойственная задача определяется как задача ЛП, вытекающая из условия:

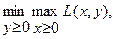(5.32)

где 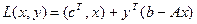- функция Лагранжа, построенная для задачи ЛП.

Подставляя значение функции Лагранжа L(x, y) в (5.32), получаем, что задача (5.32) эквивалентна задаче ЛП:

min(b^T, y); (5.33)

A^Ty ³c; (5.34)

y ³ 0. (5.35)

Данная задача называется двойственной задачей ЛП.

Сравнивая между собой прямую и двойственную к ней задачи ЛП можно сформулировать следующие правила построения задачи двойственной к данной прямой задаче:

Каждому ограничению 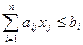, ставится в соответствие условие неотрицательности двойственной переменной y_i ³ 0. Таким образом число управляемых переменных в двойственной задаче ЛП равно m – числу ограничений в прямой задаче ЛП.

Каждой переменной x_j ³ 0 прямой задачи соответствует в двойственной задаче неравенство:

,

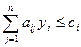где коэффициенты линейной формы c_j, 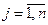служат свободными членами ограничений, а матрицей коэффициентов ограничений двойственной задачи служит матрица A^T, полученная транспонированием матрицы А. Число ограничений двойственной задачи ЛП равно n – числу управляемых переменных прямой задачи ЛП.

Максимизация линейной формы прямой задачи заменяется минимизацией линейной формы, коэффициентами которой являются свободные члены ограничений прямой задачи:

.

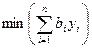Для произвольных допустимых решений x и y прямой и двойственной задач имеет место неравенство:

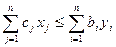. (5.36)

Сформулируем первую теорему двойственности: если одна из задач двойственной пары имеет оптимальное решение x*, то и другая задача так же разрешима – имеет оптимальное решение y*. При этом для оптимальных решений имеет место равенство:

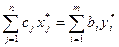. (5.37)

При исследовании пары двойственных задач имеет место одна из следующих ситуаций:

Прямая и двойственная задачи ЛП имеют допустимые решения. В этом случае обе задачи ЛП – разрешимы.

Допустимое решение имеется лишь у одной из задач двойственной пары, а область допустимых решений другой задачи ЛП – пуста. В этом случае линейная форма задачи, область допустимых решений которой не пуста, заведомо неограниченна.

Для каждой задачи двойственной пары области допустимых решений пусты. Прямая и двойственная задачи ЛП – неразрешимы.

Из первой теоремы двойственности следует условия разрешимости задачи ЛП: для разрешимости пары двойственных задач, необходимо и достаточно, чтобы область допустимых решений каждой из этих задач была непустой.

Условие разрешимости пары двойственных задач ЛП можно сформулировать с помощью второй теоремы двойственности: для того, чтобы допустимые решения x* и y* пары двойственных задач были оптимальными решениями, необходимо и достаточно, чтобы эти решения удовлетворяли условиям дополняющей нежёсткости:

;

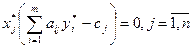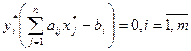. (5.38)

Основным методом решения задач линейного программирования является симплексный метод. Итерационная процедура симплексного метода состоит в переходе от некоторого вектора 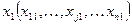к некоторому вектору 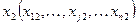так, чтобы целевая функция .

.

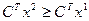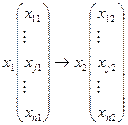Все решения ищутся для канонической формы записи ЗЛП.

Принцип решения задач линейного программирования

Точка называется крайней точкой выпуклого множества G, если через нее нельзя провести отрезок, целиком прин