Применение математических методов в энергетике для оценки статической устойчивости

Существуют следующие виды устойчивости:

а) статическая (малые изменения режимных параметров в пределах линейных отклонений)

б) динамическая (большие и, как правило, уже нелинейные отклонения)

в) результирующая (временные отклонения с последующим восстановлением нормальной синхронной работы)

Энергетический критерий статической устойчивости

У любой системы есть состояния, т.е режимы в которой система, получив случайное возбуждение, стремиться вернуться к исходному или близкому режиму и состояния, в которых случайное изменение необратимо выводит систему из исходного режима.

Пусть 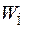– энергия потребляемая нагрузкой, 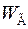– энергия источника и в исходном режиме имеет место баланс

,

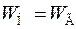который затем нарушается вследствие изменения параметра П, определяющего режим,

.

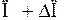Если после возмущения системы расход энергии 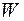растет более интенсивно, чем энергия источника 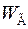после изменения параметра П, то новый режим окажется необеспеченным энергией и система будет вынуждена вернуться в исходное состояние, то есть исходный режим следует признать устойчивым.

Таким образом, условие устойчивости

,

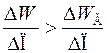где ,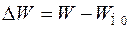

или же

.

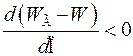Разность в числителе называется избыточной энергией

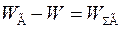
и с учетом этого критерий устойчивости приобретает вид

.

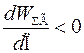В электротехнике об устойчивости судят по анализу кривых напряжения и ЭДС

,

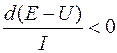в электроэнергетике по фазному углу 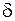. В случае простейшей энергосистемы, включающей один генератор и ШБМ, если

,

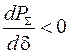где ,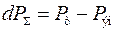

,

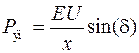E – ЭДС генератора,

U – напряжение в узле присоединения нагрузки,

x – сопротивление линии, соединяющей генерирующий и нагрузочный узлы,

– угол между векторами E и U,

то система является устойчивой.

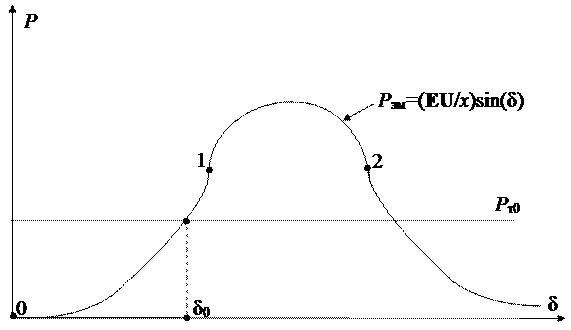
Рис. 28. Зависимость мощности выдаваемой генератором от угла

На рис. 28 участок кривой от 0 до точки 1 соответствует устойчивым режимам, от точки 1 до точки 2 – критическим режимам, режимы справа от точки 2 – неустойчивые.

В установившемся режиме при изменении угла на 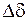, т. е. при возмущении режима появляется избыток тормозящего момента над вращающим моментом, и ротор, отклонившийся на 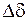, возвращается в исходное устойчивое состояние.

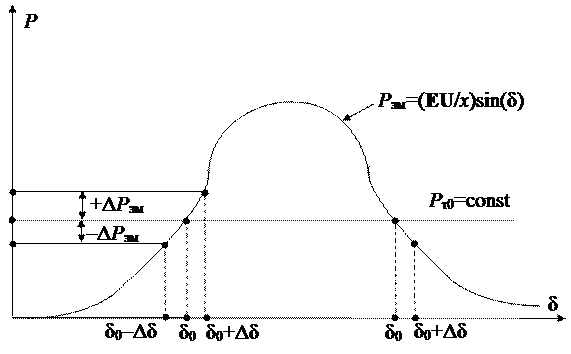
Рис. 29. Возмущения в областях устойчивых и неустойчивых режимов

Пусть изменение нагрузки носило временный характер, и возмущающее воздействие было снято. Изменение угла 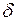вызвало временное изменение мощности выдаваемой генератором (см. рис. 29).

В случае уменьшения угла 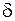в области устойчивых режимов уменьшается также и мощность, выдаваемая генератором, и, соответственно, вращающая мощность турбины, независящая от 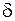, оказывается больше тормозящей ротор электромагнитной мощности

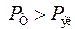
и вращающий момент больше тормозящего

.

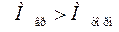Тогда ротор приобретает ускорение, что приводит к росту угла 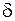и возврату в исходное устойчивое состояние.

В случае увеличения угла 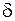в области устойчивых режимов увеличивается мощность, выдаваемая генератором, и, соответственно, вращающая мощность турбины оказывается меньше тормозящей электромагнитной мощности

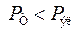
и вращающий момент меньше тормозящего

.

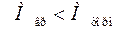Тогда ротор начинает торможение, что приводит к уменьшению угла 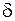и возврату в исходное устойчивое состояние.

В случае увеличения угла 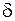в области неустойчивых режимов мощность выдаваемая генератором уменьшается, и, соответственно, вращающая мощность турбины оказывается больше тормозящей электромагнитной мощности

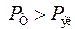
и вращающий момент больше тормозящего

.

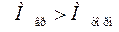Ускорение ротора приводит к еще большему росту угла 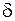и, таким образом, в данном случае можно говорить о апериодическом нарушении статической устойчивости.

Пусть изменение нагрузки носит постоянный характер, то есть после возмущения режима возмущающее действие не снято. Здесь возможны следующие варианты:

Вариант 1.

Увеличение нагрузки приводит к тому, что тормозящая ротор электромагнитная мощность, соответствующая новому увеличенному составу нагрузки, оказывается больше вращающей мощности турбины

,

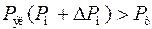тормозящий момент начинает превалировать над вращающим

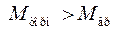
и происходит снижение скорости вращения генератора и, соответственно, частоты до тех пор, пока не восстановится баланс вращающей мощности турбины и тормозящие мощности, вследствие снижения энергопотребления нагрузки при падении частоты в соответствии с ее статической характеристикой. Баланс восстанавливается, но при новом значении частоты

f₁< f_н,

которое меньше номинального (см. рис. 30).

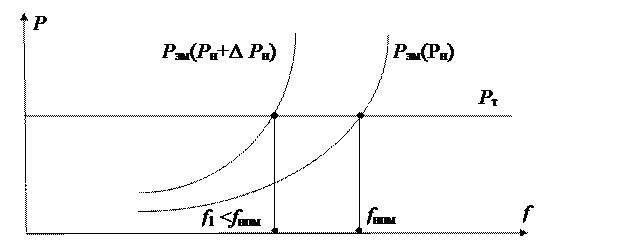
Рис. 30. Восстановление баланса за счет снижения частоты

Рис. 31. Восстановление баланса за счет увеличения расхода энергоносителя

Вариант 2.

Турбина снабжена автоматическим регулятором расхода энергоносителя, так что при увеличении нагрузки увеличивается и вращающая мощность турбины, в этом случае баланс восстанавливается, но при новом значении 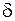, т.е. частота сохраняется неизменной, но увеличивается сдвиг фаз и режим приближается к критическому (см. рис. 31).

Таким образом, устойчивы те режимы, при возмущении которых факторы, стремящиеся к их восстановлению, растут интенсивнее, чем факторы, противодействующие этому восстановлению. Любой устойчивый режим можно сделать неустойчивым путем увеличения нагрузки (утяжеления).

На рис. 32 факторы нарушающие устойчивость обозначены как Н, факторы, стремящиеся к ее восстановлению – как В. При этом режим является устойчивым при

,

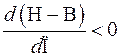неустойчивым если

,

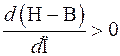критическим при выполнении условия

.

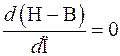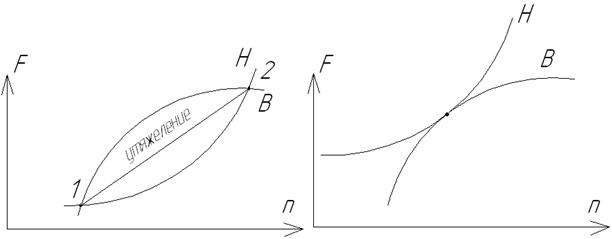
Рис. 32. Устойчивый, неустойчивый и критический режимы

Сопоставление параметров критического 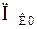и исследуемого устойчивого 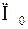режимов определяет коэффициент запаса статической устойчивости

.

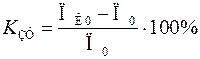Статическая устойчивость – это способность системы восстанавливать исходный режим при малом его возмущении или режим, близкий к исходному, если возмущающее действие не снято.

Строгое решение задачи проверки статической устойчивости требует:

1) Составление системы линеаризованных дифференциальных уравнений малых колебаний для всех элементов системы

.

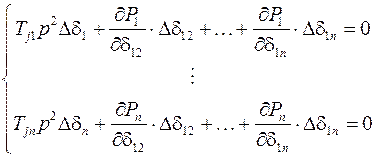или же в матричной форме

.

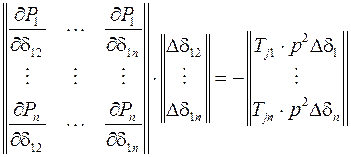2) Составление характеристического уравнения, полученного приравниванием к нулю определителя квадратной матрицы системы

.

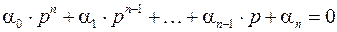Если все действительные корни и вещественные части всех комплексных корней отрицательны, то система устойчива.

Наличие хотя бы одного комплексного корня с положительной вещественной частью соответствует явлению самораскачивания (см. рис. 33).

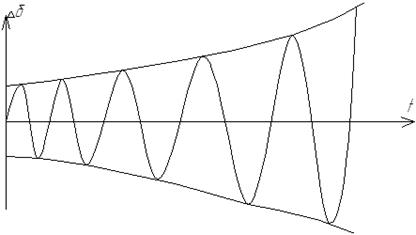
Рис. 33. Колебательное нарушение статической устойчивости

Наличие хотя бы одного положительного действительного корня означает апериодический уход от исходного режима, т.е. происходит апериодическое нарушение статической устойчивости (см. рис. 34).

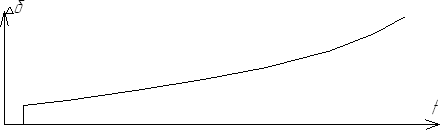
Рис. 34. Апериодическое нарушение статической устойчивости

Применение метода малых колебаний на примере простейшей одногенераторной энергосистемы

При сохранении установившегося режима уравнение движения ротора генератора в случае одногенераторной энергосистемы имеет вид

.

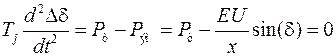При нарушении установившегося режима, данное уравнение может быть разложено в ряд Тейлора по малому приращение фазного угла 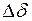в окрестностях исходного значения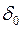

,

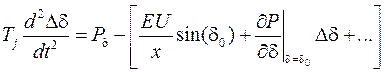что с учетом

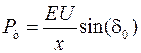
и пренебрежением слагаемыми ряда Тейлора, включающих производные выше первой, позволяет записать уравнение малых колебаний ротора

.

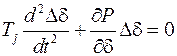При введение оператора 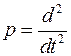принимаемого в качестве алгебраической величины данное уравнение можно записать в операторной форме

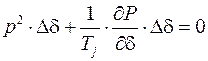
или же

.

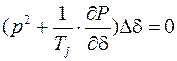Поскольку приращение сдвига фаз при возмущении режима

,

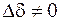следовательно

.

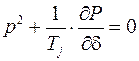Полученное уравнение является характеристическим для рассматриваемой системы и из условия

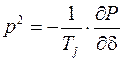
можно определить его корни

.

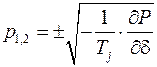Решение характеристического уравнения имеет вид

.

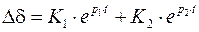Здесь возможны два случая:

1) ,

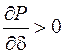подкоренное выражение отрицательно и корни мнимые

,

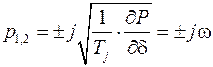что соответствует уравнение незатухающих гармонических колебаний (с учетом неизбежного демпфирования – затухающих)

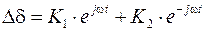
2) ,

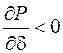подкоренное выражение положительно и имеют место два действительных корня

.

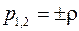поскольку один из корней положительный это соответствует апериодическому нарушению статической устойчивости

.

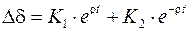Применение метода малых колебаний для анализа

статической устойчивости сложной энергосистемы

В сложной энергосистеме мощность, выдаваемая генератором, зависит от модулей и фаз всех остальных генераторов. Полный ток, протекающий в цепи первого из n генераторов, определяется по следующей формуле

.

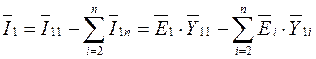Мощность, выдаваемая первым генератором из n генераторов

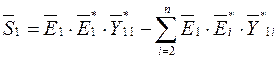
при записи комплексных параметров через показательные степени

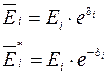
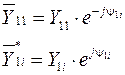
выражение для мощности первого из n генераторов может быть записано в виде

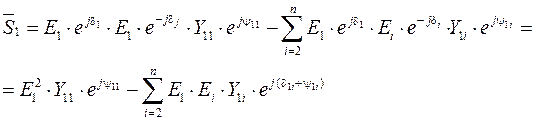
или же при переходе к тригонометрической форме записи

,

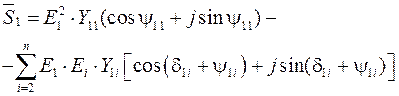где 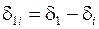– относительный фазный угол между векторами ЭДС первого и i-го генераторов.

Таким образом, в сложной энергосистеме активная мощность, выдаваемая каждым из n генераторов зависит от модулей и фаз ЭДС всех остальных генераторов

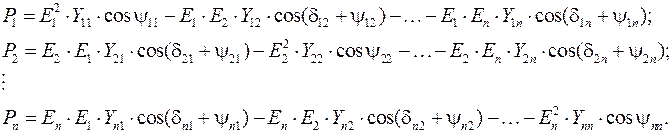В системе из n-генераторов имеется только (n-1) независимых относительных фазных углов, остальные же могут быть выражены через независимые

.

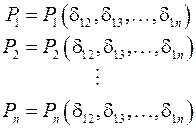При нарушении установившегося режима возникает качание роторов генераторов, которое определяется из системы уравнений малых колебаний

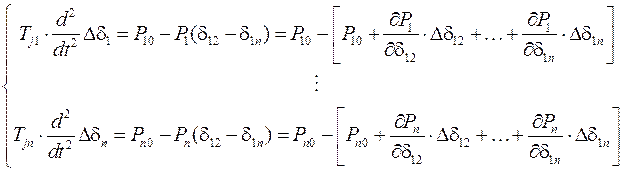
или же

.

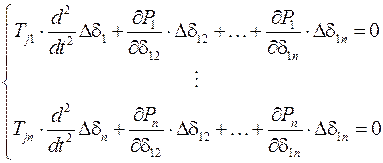Если поделить все уравнения системы на соответствующие 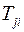и поочередно вычесть их из первого уравнения, то при введении коэффициентов

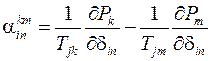
и принятии оператора 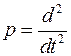в качестве алгебраической величины,

вышеприведенная система может быть переписана в операторной форме

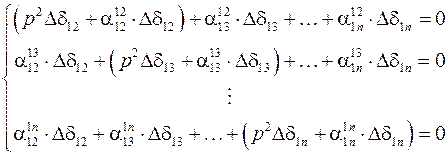
и в матричной форме

,

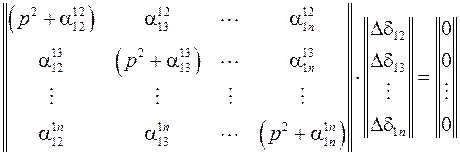позволяющей вынести все малые приращения независимых относительных фазных углов в отдельный столбец. Определитель квадратной матрицы, являющейся сомножителем данного столбца называется характеристическим определителем

.

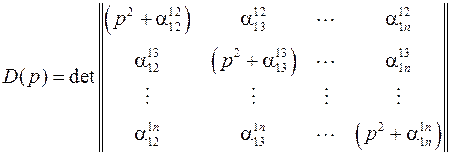Независимые относительные фазные углы могут быть найдены по правилу Крамера

,

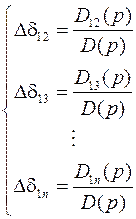где D_1i(p) – определитель вышеуказанной квадратной матрицы, в которой i-й столбец заменен нулями из правой части системы уравнений.

Признак нарушения устойчивости – неограниченный рост хотя бы одного из относительных фазных углов.

Критерий Гурвица статической устойчивости

в сложной электроэнергетической системе

Как уже упоминалось выше, режим системы является устойчивым, если все корни характеристического уравнения отрицательны. Если все корни отрицательные, то система статически устойчива. График зависимости угла отклонения ротора от синхронной оси отсчета при статической устойчивости системы отображен на рис.35.

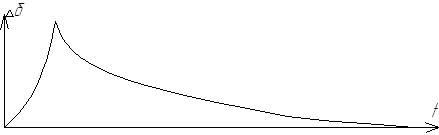
Рис. 35. Зависимость 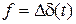при статически устойчивой системе

Если хотя бы один действительный корень положительный, то наблюдается апериодическое нарушение статической устойчивости. Кривая зависимости угла отклонения ротора от синхронной оси отсчета при апериодическом нарушении статической устойчивости системы представлена на рис.36.

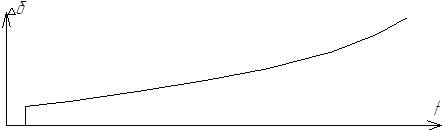
Рис. 36. Зависимость 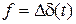при апериодическом нарушении устойчивости

Если хотя бы одна пара комплексно сопряженных корней имеет положительные вещественные части, то наблюдается колебательное нарушение статической устойчивости. Зависимость угла отклонения ротора от синхронной оси отсчета при колебательном нарушении устойчивости изображена на рис.37.

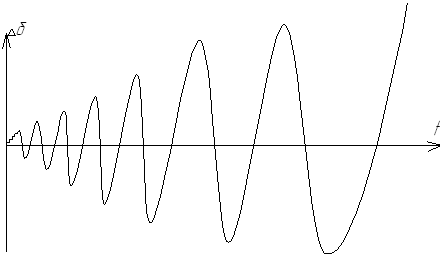
Рис. 37. Зависимость 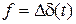при колебательном нарушении устойчивости

Согласно критерию Гурвица все корни характеристического уравнения отрицательны если:

а)все коэффициенты характеристического уравнения положительные;

б)все определители Гурвица положительные.

Всего вычисляется n определителей Гурвица 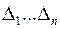, где 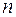– порядок характеристического уравнения.

первый определитель Гурвица

,

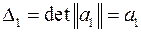второй определитель Гурвица

,

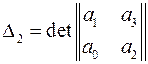третий определитель Гурвица

,

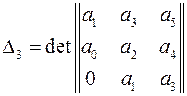n-й определитель Гурвица

,

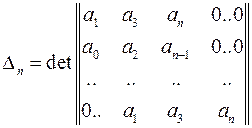Определитель Гурвица k-го порядка представляет собой определитель квадратной матрицы размером 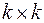, в верхнем левом углу которого находится коэффициент характеристического уравнения 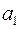, вдоль строки слева направо индекс коэффициентов увеличивается на два через каждую позицию, вдоль столбца сверху вниз индекс коэффициента уменьшается на единицу через каждую позицию.

Коэффициенты, индексы которых меньше нуля или больше n, замещаются на нуль. Определители вычисляются по формуле

,

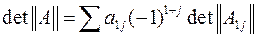где 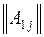– матрица, полученная из исходной, путем вычеркивания первой строки и j-го столбца.

Например, для характеристического уравнения третьего порядка ,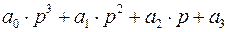

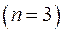
определители Гурвица имеют вид

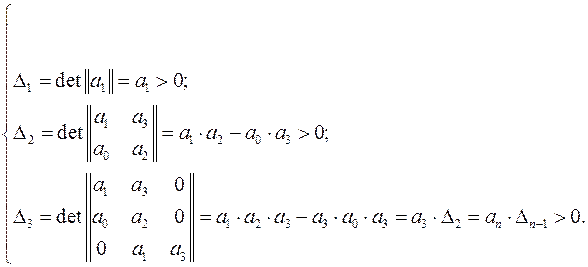
Т.к. в определителе 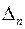(в данном примере 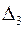) находится только один элемент 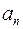в последнем столбце (в данном примере 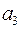), то условие прохождения 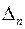через нуль (предел статической устойчивости) разбивается на два под-условия:

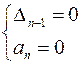
При утяжелении режима из заведомо устойчивой области, прохождение через нуль 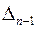соответствует пределу колебательной статической устойчивости.

Переход через нуль свободного члена характеристического уравнения

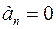
соответствует пределу апериодической статической устойчивости.

Метод Михайлова проверки статической устойчивости сложной энергосистемы

Метод Михайлова заключается в графической интерпретации критерия статической устойчивойсти. Корни характеристического уравнения могут находиться в различных сочетаниях на комплексной плоскости, возможные варианты отображены на рис.38.

Рис. 38. Возможные варианты расположения корней уравнения

Если все корни лежат в левой полуплоскости, система устойчива, если хотя бы один действительный корень находится в правой полуплоскости, то это означает апериодическое нарушение статической устойчивости, наличие пары комплексно сопряженных корней с положительной вещественной частью означает колебательное нарушение статической устойчивости системы.

Характеристическое уравнение

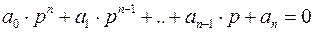
может быть также записано в виде

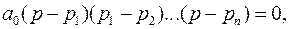
где пределстатической ждени лемент в последнем столбце ( первой строки и озицию вдоль столбцаи, то наблюдается колебательное наруше 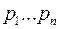– неизвестные корни;

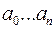– известные коэффициенты.

Вектор

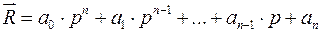
является комплексным и может быть отображен на комплексной плоскости, при замене

,

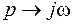где 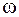– вещественное число. Метод Михайлова позволяет судить об устойчивости системы по изменению угла вектора 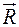относительно оси абсцисс при изменении 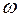от нуля до бесконечности.

Пусть один действительный корень располагается в левой полуплоскости (см рис.39).

Отрицательный действительный корень дает вектору 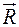поворот на 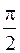в направлении против часовой стрелки при изменении 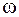от 0 до .

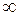Рис. 39. Изображение отрицательного действительного корня на комплексной плоскости

Пара комплексно сопряженных корней с отрицательной вещественной частью дает вектору 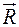поворот на 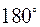в направлении против часовой стрелки при изменении 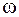от 0 до 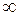(см. рис. 40).

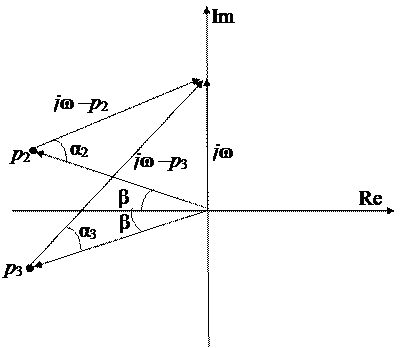
Рис. 40. Изображение пары комплексно сопряженных корней на комплексной плоскости

Если имеется 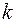корней в левой полуплоскости, то при изменении 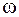от 0 до 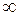вектор 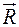совершает поворот в направлении против часовой стрелки на 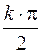, принимаемым за положительное.

Если имеется 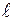корней в правой полуплоскости, то при изменении 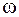от 0 до 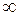вектор 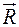совершает поворот по часовой стрелке (в отрицательном направлении) на .

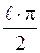Если имеется 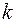корней в левой полуплоскости и 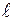корней в правой полуплоскости, то при изменении 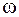от 0 до 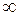вектор 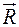совершает поворот на 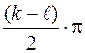в положительном направлении.

Если в выражении

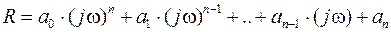
менять значение 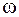от 0 до 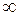, графически отображая при этом перемещения точки (т.е. строить годограф), то, зная полное число корней 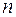, можно сформулировать критерий устойчивости Михайлова

,

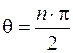где 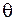– поворот вектора 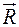при изменении 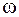от 0 до ,

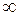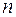– число корней.

Если 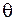принимает значения

,

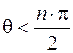следовательно система неустойчива.

В случае если при изменении 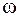от 0 до 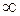полный поворот 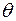вектора 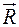в положительном направлении составляет s четвертей комплексной полуплоскости и s меньше числа корней n

,

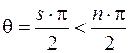из условия

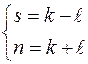
можно определить число корней в левой 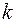и правой полуплоскостях :

.

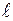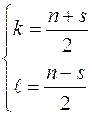Пример использования метода Михайлова для анализа статической устойчивости одногенераторной системы

Простейшая энергосистема, включающая один генератор, узел присоединения нагрузки и линию, соединяющую генераторный и нагрузочный узел, изображена на рис.41.

Рис. 41. Схема одногенераторной системы

Уравнение движения ротора в данном примере:

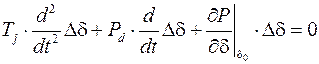
где 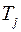– постоянная инерции ротора;

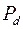– коэффициент демпфирования;

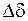– отклонение фазного угла от синхронной оси;

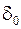– значение фазного угла в исходном устойчивом состоянии.

Если взять производную в третьем слагаемом

,

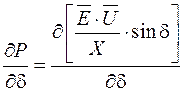перейти к операторной форме

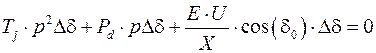
и учесть неравенство

,

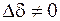то полученное выражение будет являться характеристическим уравнением для данной системы:

.

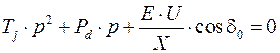Его также можно записать в виде

,

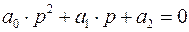где

.

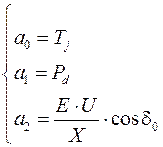Для того, что бы вектор 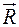мог быть отображен на комплексной плоскости, производится замена 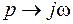. При этом характеристическое уравнение

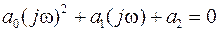
и вектор 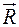приобретают форму, в которой легко выделить действительные и мнимые части по четным и нечетным степенным мнимой единицы

.

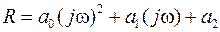Метод Михайлова позволяет судить не только о факте наличия или отсутствие устойчивости, но и определять вид неустойчивости по соотношению числа корней в левой и правой полуплоскостях (пример для уравнения второго порядка см. табл. 1)

Табл. 1. Состояние статической устойчивости системы

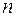
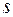
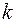
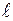
угол поворота					вывод
					статическая устойчивость
–180		-2			колебательное нарушение статической устойчивости
					апериодическое нарушение статической устойчивости

Применение метода D-разбиения для оценки статической устойчивости

Данный метод применяется в тех случаях, когда необходимо оценить влияние на устойчивость какого-либо параметра системы (например, коэффициента усиления регулятора возбуждения).

Методом D-разбиения находится такое значение коэффициента усиления или какого-либо иного параметра, при которых характеристическое уравнение автоматически регулируемой системы имело бы корни только с отрицательными вещественными частями.

В зависимости от числа параметров различают метод D-разбиения по одному, двум и более параметрам.

1) Метод D-разбиения по одному параметру.

Если часть коэффициентов характеристического уравнения

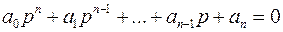
линейно зависят от параметра K системы автоматического регулирования, то оно может быть представлено в следующем виде

,

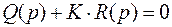где 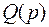– это совокупность слагаемых характеристического уравнения, не зависящих от K.

В таком случае K может быть определено из выражения

.

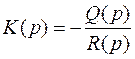При замене 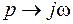оно приобретает вид

.

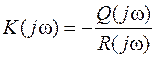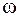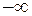Меняя от до 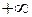с шагом 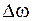вычисляется ряд значений 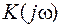. Кривая, построенная по этим значениям на комплексной плоскости параметра K называется D-кривой.

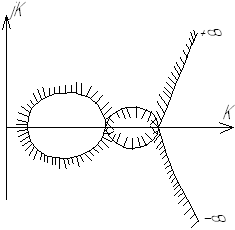
D-кривая делит комплексную плоскость параметра K на области с одинаковым числом корней в правой полуплоскости, т.е. с положительными вещественными частями (см. рис. 42).

Если параметр K пересекает D-кривую с заштрихованной стороны, то характеристическое уравнение теряет один корень в левой полуплоскости и приобретает в правой. При пересечении с незаштрихованной стороны один корень характеристического уравнения перемещается из правой полуплоскости в левую.

m

Рис. 42. D-кривая

На рис. 42 m – число корней в правой полуплоскости, имеющие положительные вещественные части.

При анализе статической устойчивости выбирается область с минимальным значением m и она становится претендентом на область устойчивости. Для проверки необходимо задаться значением K в этой области, подставить в характеристическое уравнение и проверить знаки его корней одним из выше рассмотренных критериев (метод Михайлова, метод Гурвица)

Для сложной энергосистемы характеристический определитель записывается в виде суммы трех определителей с двумя настроечными коэффициентами

,

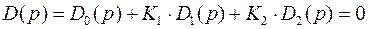где 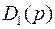– соответствует совокупности слагаемых характеристического уравнения, коэффициенты которых линейно зависят от 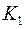; 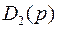– соответствует совокупности слагаемых характеристического уравнения, коэффициенты которых линейно зависят от ;

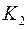При замене 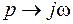, данное выражение приобретает вид

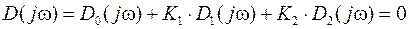
позволяющий выделить действительные и мнимые части

,

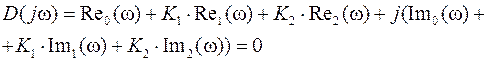где 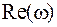– соответствует совокупности слагаемых характеристического уравнения находящихся на действительной оси, имеющих четную степень 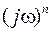, где n – четное число, что исключает мнимую единицу ;

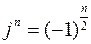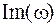– соответствует совокупности слагаемых характеристического уравнения, имеющих нечетную степень 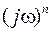, где n – нечетное число, которые лежат на мнимой оси, поскольку .

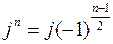Данное выражение можно записать в виде системы уравнений

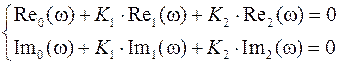
или же в матричной форме

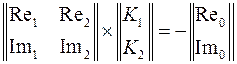
Согласно правилу Крамера, параметр 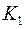определяется из выражения

,

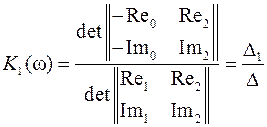параметр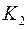

.

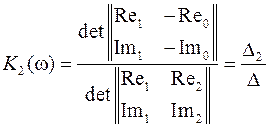Решение есть если все определители отличны от нуля

,

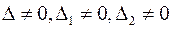в случае обнуления знаменателя

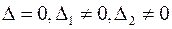
решения нет, так как k стремится к бесконечности, в случае обнуления всех определителей

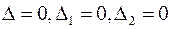
раскрываются неопределенности вида и получается система линейно зависимых уравнений.

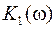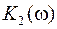По зависимостям и на комплексной плоскости строятся кривые D-разбиения, изображенные на рис. 43.

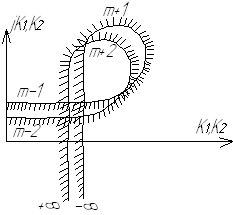
Рис. 43. Кривые D-разбиения

Статическая устойчивость и сходимость

итерационного процесса при расчете

установившегося режима

Применение ЭВМ для расчета установившегося режима и анализа статической устойчивости вызвало интерес взаимосвязи этих проблем.

Якобиан системы уравнений установившегося режима совпадает со свободными членами характеристического уравнения при выполнении следующих условий:

1) в качестве независимых переменных в генерирующих узлах выбирается активная мощность и модули напряжения;

2) генераторы и нагрузки заданы теми же статическими характеристиками, что и при анализе статической устойчивости;

3) в качестве балансирующего узла выбраны шины бесконечной мощности.

Таким образом,при расчете установившегося режима методом Ньютона можно оценить статическую устойчивость без дополнительных вычислений.

Это можно продемонстрировать на примере простой энергосистемы из трех узлов (см. рис. 44), результат будет верен и для общего случая.

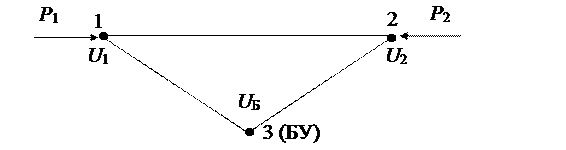
Рис.44. Система из трех узлов

При решении системы уравнений установившегося режима

,

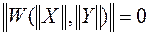где

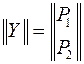– активные мощности, потребляемые/генерируемые в узлах – независимые параметры,

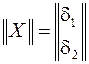– фазы узловых напряжений – искомые, зависимые параметры, начальные приближения которых ,

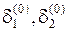первая итерация метода Ньютона в общем случае имеет вид

,

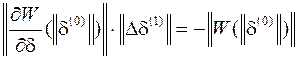где

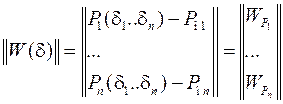– небаланс мощности,

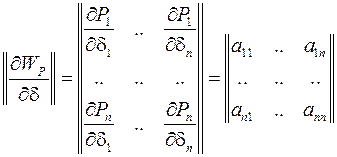– матрица производных небалансов по искомым параметрам – по фазам узловых напряжений,

где .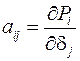

Система уравнений малых колебаний

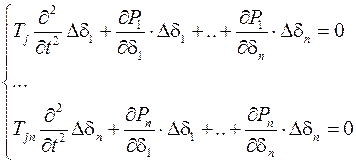
в матричной операторной форме в общем случае имеет вид

,

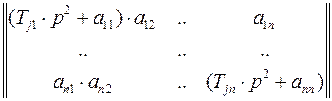где также .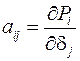

Для рассматриваемого примера (число независимых узлов 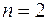) свободный член характеристического уравнения может быть найден при раскрытии определителя данной матрицы второго порядка

,

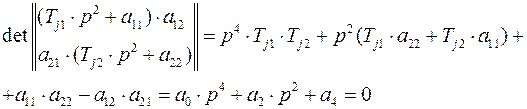где 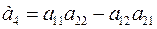– свободный член характеристического уравнения. В тоже время якобиан системы уравнений установившегося режима для данного примера определяется из равенства

,

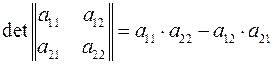то есть совпадает со свободным членом характеристического уравнения

Если при движении из области устойчивого начального приближения (в котором свободный член не равен нулю), свободный член обнуляется, следовательно, один из корней характеристического уравнения проходит через нуль, т.е. меняет знак, что в свою очередь означает утрату системой статической устойчивости.

Таким образом, если ни в одной точке итерационного процесса метода Ньютона якобиан системы уравнений установившегося режима, соответствующий свободному члену характеристического уравнения, не сменил знак, и режим в точке начального приближения был устойчив, то и расчетный режим так же будет апериодически устойчив.

Постоянство знака якобиана при движении по кривой сходящегося итерационного процесса из области устойчивого начального приближения является достаточным условием апериодической устойчивости.

Если знаки якобиана в точке начального приближения, соответствующего устойчивому режиму и в точке расчетного режима различны, это является достаточным условием апериодической неустойчивости.

Определение режимов

предельных по апериодической