Апериодическое (инерционное) звено первого порядка

Апериодическим звеном первого порядка называют звено, которое описывается уравнением

(Tp+1)x(t) = kg(t) (7.1)

или передаточной функцией

W (s) = k/(Ts + 1). (7.2)

Это звено также называют инерционным звеном или инерционным звеном первого порядка. Апериодическое звено в отличие от вышерассмотренных звеньев характеризуется двумя параметрами: постоянной времени Т и передаточным коэффициентом k.

Частотная передаточная функция

W (jω) = k/(Tjω + 1). (7.3)

Умножив числитель и знаменатель на комплексно-сопряженное знаменателю число, получим

U (ω)= k/[(Tω)2+1]; V (ω) = - kTω/[(Tω)2 + 1)]. (7.4)

Амплитудную и фазовую частотные функции можно определить, воспользовавшись правилом модулей и аргументов. Так как модуль числителя частотной передаточной функции (7.3) равен k, а модуль

знаменателя 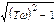, то

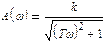(7.5)

Аргумент числителя W (jω) равен нулю, а аргумент знаменателя arctg ωT поэтому φ(ω) = arg W (jw) = — arctg ωТ. Из (7.5) следует:

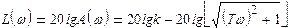(7.6)

Решив дифференциальное уравнение (7.2) при и = 1(t) и нулевом начальном условии (х (0) = 0), получим h (t) = k (1 – e-t/T ). Весовая функция

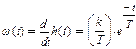(7.7)

АФЧХ апериодического звена (рисунок 7.1, а) есть полуокружность, в чем нетрудно убедиться, исключив из параметрических уравнений (7.4) АФЧХ частоту.

Логарифмическая амплитудно-частотная характеристика представлена на рисунке 7.1, б. На практике обычно ограничиваются построением так называемой асимптотической ЛАЧХ (ломаная линия на том же рисунке 7.1, б). Только в критических случаях, когда небольшая погрешность может повлиять на выводы, рассматривают точную ЛАЧХ.

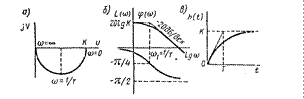
Рисунок 7.1 – Частотные и переходная характеристики апериодического звена первого порядка

Частоту ω1 = 1/Т, при которой пересекаются асимптоты, называют сопрягающей. Точная и асимптотическая ЛАЧХ наиболее сильно отличаются при сопрягающей частоте; отклонение при этой частоте примерно равно 3 дБ.

Уравнение асимптотической ЛАЧХ имеет вид

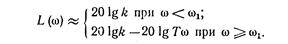
Оно получается из уравнения (7.6), если в нем под корнем при ω <ω1 пренебречь первым слагаемым, а при ω > ω1 — вторым слагаемым. Согласно полученному уравнению, асимптотическую ЛАЧХ можно строить следующим образом: на уровне L (ω) = 20 lg k до частоты ω = ω1 провести прямую, параллельно оси частот, а далее через точку с координатами ω = ω1 и L (ω) = 20 lg k — прямую под наклоном — 20 дБ/дек.

По АФЧХ или ЛАЧХ легко определить параметры Т и k апериодического звена (рисунок 7.1).

Логарифмическая фазовая частотная характеристика изображена на рисунке 7.1, б. Эта характеристика асимптотически стремится к нулю при ω → 0 и к -π/2 при ω → ¥. При ω = ω1, фазовая частотная функция принимает значение — π/4, т. e. φ(ω1) = - π/4. ЛФЧХ всех апериодических звеньев имеют одинаковую форму и могут быть получены по какой-либо одной характеристике параллельным сдвигом вдоль оси частот влево или вправо в зависимости от постоянной времени Т. Поэтому для построения ЛФЧХ апериодического звена можно воспользоваться шаблоном или номограммой (рисунок 7.1, г).

Переходная характеристика апериодического звена (рисунок 7.1, а) представляет собой экспоненциальную кривую. По ней можно определить параметры: передаточный коэффициент, равный установившемуся значению h(¥); постоянную времени, равную значению t, соответствующему точке пересечения касательной к характеристике в начале координат с ее асимптотой (рисунок 7.1, в).