Частотные характеристики АСР и У
Принцип суперпозиции
Для оценки установившихся режимов оказалось удобным рассматривать поведение элементов и систем при воздействиях, являющихся периодическими функциями времени. В качестве таких воздействий были выбраны гармонические воздействия, что обусловлено несколькими обстоятельствами. Во-первых, большинство реально встречающихся воздействий может быть представлено в виде суммы гармоник различных частот (разложение Фурье). Во-вторых, в установившихся режимах гармонические сигналы передаются линейными элементами и системами без искажений. И в-третьих, обычно не возникает затруднений в экспериментальном исследовании поведения линейных элементов и систем при гармонических воздействиях.
Важное значение при описании линейных стационарных систем (звеньев) имеют частотные характеристики. Они получается при рассмотрении вынужденных движений системы (звена) при подаче на ее вход гармонического воздействия.
Для линейных систем справедлив принцип суперпозиции, который можно сформулировать следующим образом: реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности. Это позволяет ограничиться изучением систем только с одним входом.
Частотная передаточная функция
В общем случае уравнение линейной стационарной системы с одним входом можно записать так:
(a0pn+a1pn-1+…+an)x = (b0pm+b1pm-1+…+bm)g (4.1)
Ее передаточная функция по определению
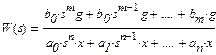 (4.2)
(4.2)
Функцию W(jω), которую получают из передаточной функции при подстановке в нее р = jω
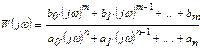 (4.3)
(4.3)
называют частотной передаточной функцией. Частотная передаточная функция является комплекснозначной функцией от действительной переменной ω, которая называется частотой. Функцию W(jω) можно представить в виде
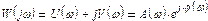
где
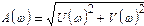 ;
;
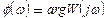 ;
;
Если
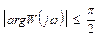 , то
, то 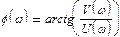 (4.4)
(4.4)
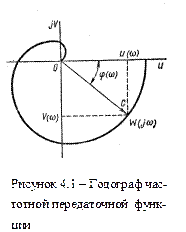 На комплексной плоскости (рисунок 4.1) частотная передаточная функция W(jω) определяет вектор ОС, длина которого равна А (ω), а аргумент (угол, образованный этим вектором с действительной положительной полуосью) — φ(ω). Кривую, которую описывает конец этого вектора при изменении частоты от 0 до ∞ (иногда от — ∞ до ∞), называют амплитудно-фазовой частотной характеристикой (АФЧХ).
На комплексной плоскости (рисунок 4.1) частотная передаточная функция W(jω) определяет вектор ОС, длина которого равна А (ω), а аргумент (угол, образованный этим вектором с действительной положительной полуосью) — φ(ω). Кривую, которую описывает конец этого вектора при изменении частоты от 0 до ∞ (иногда от — ∞ до ∞), называют амплитудно-фазовой частотной характеристикой (АФЧХ).
Частотную передаточную функцию будем называть также амплитудно-фазовой частотной функцией. Ее действительную часть U (ω) = Re W(jw) и мнимую часть V (ω) = ImW(jω) будем называть соответственно вещественной и мнимой частотной функцией. График вещественной частотной функции (кривая зависимости U = U (ω)) называют вещественной частотной характеристикой, а график мнимой частотной функции—мнимой частотной характеристикой.
Модуль А(ω) = |W(jω)| называют амплитудной частотной функцией, ее график — амплитудной частотной характеристикой.
Аргументу φ(ω)= arg W (jω) называют фазовой частотной функцией, ее график — фазовой частотной характеристикой.
Логарифмическая амплитудная и фазовая частотные характеристики
Кроме перечисленных частотных характеристик используют еще логарифмические частотные характеристики (ЛЧХ) — логарифмические амплитудные частотные характеристики (ЛАЧХ) и логарифмические фазовые частотные характеристики (ЛФЧХ). Назовем функцию
L(ω) = 20 lg A(ω) = 20 lg|W(jω)| (4.5)
логарифмической амплитудной частотной функцией. График зависимости логарифмической амплитудной частотной функции L(ω) от логарифма частоты (lgω) называют логарифмической амплитудной частотной характеристикой (ЛАЧХ). При построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе: на отметке, соответствующей значению lgω, пишут само значение ω, а не значение lgω, а по оси ординат — L(ω). Логарифмической фазовой частотной характеристикой (ЛФЧХ) называют график зависимости фазовой частотной функции φ(ω) от логарифма частоты lgω. При его построении по оси абсцисс, как и при построении ЛАЧХ, на отметке, соответствующей значению lgω, пишут значение ω.
Единицей L(ω) является децибел, а единицей логарифма частоты в ЛЧХ — декада. Декадой называют интервал, на котором частота изменяется в 10 раз. При изменении частоты в 10 раз говорят, что она изменилась на одну декаду.
Ось ординат при построении ЛЧХ проводят через произвольную точку, а не через точку ω = 0. Частоте ω = 0 соответствует бесконечно удаленная точка: lg ω → — ∞ при ω → 0.
При построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе. Отрезок оси абсцисс, соответствующий изменению частоты в 10 раз, называется декадой, а отрезок, соответствующий изменению частоты в 2 раза, — октавой.
По оси ординат ЛАЧХ откладывают при равномерном масштабе логарифмическую амплитуду
L = 20 lg A дБ.
Нуль логарифмической амплитуды соответствует A = 1.
Нуль оси абсцисс лежит слева в бесконечности, так как lg 0 = —∞, поэтому ось ординат может пересекать ось абсцисс в любой точке. Эту точку выбирают так, чтобы график охватывал нужный диапазон частот.
У ЛФЧХ такая же ось абсцисс, а по оси ординат в равномерном масштабе откладывают фазу φ(ω) в градусах (или радианах).
ЛФЧХ строят обычно под ЛАЧХ с тем, чтобы изменение фазы можно было сопоставить с изменением амплитуды. Оси абсцисс ЛАЧХ и ЛФЧХ можно совмещать.
Логарифмические частотные характеристики удобны тем, что небольшим графиком может быть охвачен широкий диапазон частот. При этом одинаково наглядно изменение частотных свойств как на малых, так на средних и высоких частотах. Небольшим графиком охватывается и широкий диапазон изменения амплитуды с одинаковой наглядностью изменения больших и малых амплитуд.
Кроме того, оказывается, что значительные участки ЛАЧХ с большой точностью могут быть заменены прямыми линиями — асимптотами. Они имеют отрицательный и положительный наклон, кратный 20 дБ/дек, т. е. 0 дБ/дек, — 20 дБ/дек, —40 дБ/дек, ..., а также +20 дБ/дек, +40 дБ/дек, ...,
В ряде случаев оказывается возможным пренебречь кривизной ЛАЧХ на отдельных небольших участках частот. Тогда ЛАЧХ изображается отрезками прямых (асимптотами) и называется асимптотической ЛАЧХ. Для ее построения нужны лишь весьма простые вычисления.
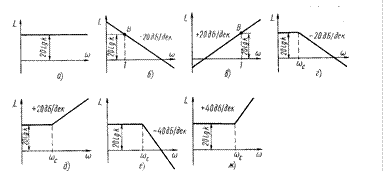
Рисунок 4.2 - Типовые асимптотические ЛАЧХ
Наиболее характерный вид имеют ЛАЧХ при следующих значениях модуля А частотной передаточной функции:
а) А = k. В этом случае L = 20 lg k есть постоянная величина и ЛАЧХ представляет собой прямую, параллельную оси абсцисс (рисунок 4.2, a);
б) А = k/ω. В этом случае L = 20 lg k — 20 lgω. При ω = 1 имеем L = =20lg k и на протяжении одной декады (с увеличением ω в 10 раз) L уменьшается на 20 дБ. ЛАЧХ представляет собой прямую с наклоном —20 дБ/дек, проходящую через точку В с координатами [1; 20 lg k] (рисунок 4.2, б);
в) A = kω. В этом случае L = 20 lg k + 20 lg ω. Так же как и в предыдущем случае, при ω = 1 имеем L = 20 lg k. Затем, с увеличением ω, увеличивается и L на 20 дБ/дек. ЛАЧХ есть прямая с наклоном +20 дБ/дек, проходящая через точку В c координатами [1; 20 lg k] (рисунок 4.2, в);
г) 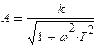 . В этом случае L = 20 lg k — 10 lg (1 + ω2T2)
. В этом случае L = 20 lg k — 10 lg (1 + ω2T2)
При малых частотах ω2T2 << 1 имеем L ≈ 20 lg k. Это низкочастотная асимптота, параллельная оси абсцисс. При больших частотах ω2T2 >>1 имеем L ≈ 20 lg k — 20 lg ωT. Это высокочастотная асимптота, которая уменьшается на 20 дБ/дек. Следовательно, асимптотическая ЛАЧХ образуется двумя асимптотами, которые сопрягаются при частоте ωc = 1/T (рисунок 4.2, г), так как при этой частоте удовлетворяются уравнения обеих асимптот;
д) 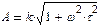 . В этом случае L = 20 lg k + 10 lg (1 + ω2τ2). Как и в предыдущем случае, асимптотическая ЛАЧХ составляется двумя асимптотами, которые сопрягаются при частоте ωс = 1/τ, но высокочастотная асимптота имеет положительный наклон (рисунок 4.2, д);
. В этом случае L = 20 lg k + 10 lg (1 + ω2τ2). Как и в предыдущем случае, асимптотическая ЛАЧХ составляется двумя асимптотами, которые сопрягаются при частоте ωс = 1/τ, но высокочастотная асимптота имеет положительный наклон (рисунок 4.2, д);
е) 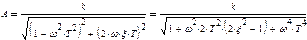 ,
,
где ξ < 1. В данном случае L = 20 lg k — 10 lg [ 1 + 2ω2 T2 (2ξ2 — 1) + ω4T4]. На малых частотах L ≈ 20 lg k и на высоких частотах L ≈ 20 lg k — 40lgωT. Асимптотическая ЛАЧХ, как и в двух предыдущих случаях, составляется двумя асимптотами, которые сопрягаются при частоте ωc=1/T. Низкочастотная асимптота параллельна оси абсцисс, а высокочастотная имеет отрицательный наклон и уменьшается на 40 дБ/дек (рисунок 4.2, е);
ж) 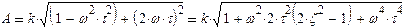 , где ζ< 1. В этом случае L = 20 lg k + 10 lg [1 + 2ω2τ2(2ζ2-1)+ω4τ4].
, где ζ< 1. В этом случае L = 20 lg k + 10 lg [1 + 2ω2τ2(2ζ2-1)+ω4τ4].
Асимптотическая ЛАЧХ опять составляется двумя асимптотами, которые сопрягаются при частоте ωc = 1/τ. Низкочастотная асимптота L ≈ 20 lg k параллельна оси абсцисс, а высокочастотная L ≈ 20 lg k + 40 lg ωτ имеет положительный наклон — увеличивается на 40 дБ/дек (рисунок 4.2, ж).
Физический смысл частотных характеристик
При гармоническом воздействии (g(t) = gmcos ωt) в устойчивых системах после окончания переходного процесса, выходная величина также изменяется по гармоническому закону, но с другими амплитудой и фазой. При этом отношение амплитуд выходной и входной величин, равно модулю, а сдвиг фазы — аргументу частотной передаточной функции. И, следовательно, амплитудная частотная характеристика показывает изменение отношения амплитуд, а фазовая частотная характеристика—сдвиг фазы выходной величины относительно входной в зависимости от частоты входного гармонического воздействия.
Из приведенной физической интерпретации частотных характеристик ясно, как строить их экспериментальным путем. Для экспериментального построения частотных характеристик имеется специальная аппаратура, в состав которой входят генератор гармонических колебаний с регулируемой частотой и устройства для измерения амплитуды и фазы колебаний.
Частотные характеристики используют для описания как устойчивых, так и неустойчивых систем. Но в последнем случае они не имеют такого ясного физического смысла.
На основании равенств (4.4) легко составить соотношения, связывающие частотные характеристики одну с другой:
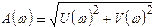 ;
;
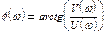 ;
;
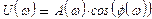 ;
;
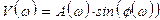 .
.
Полезно заметить, что вещественная частотная характеристика есть четная функция частоты ω, мнимая частотная характеристика — нечетная функция:
U (-ω) = U (ω), V (-ω) = -V (ω)
Дата добавления: 2022-07-20; просмотров: 520;











